신발끈 공식(shoelace formula) 또는 신발끈 알고리듬(shoelace algorithm) (역시 가우스의 넓이 공식 및 측량사의 공식(surveyor's formula)으로 알려짐)은 그것의 꼭짓점이 평면에서 데카르트 좌표(Cartesian coordinates)에 의해 설명되는 단순 다각형(simple polygon)의 넓이(area)를 결정하는 수학적 알고리듬(algorithm)입니다. 사용자는 해당 좌표를 교차-곱(cross-multiplies)하여 다각형(polygon)을 에워싸는 넓이를 찾고, 둘러싸는 다각형에서 이것을 빼서 다각형 내부의 넓이를 찾습니다. 그것은 신발끈 공식으로 불리는데 왜냐하면 신발끈을 꿰는 것과 같이 다각형을 구성하는 좌표에 대해 일정한 교차-곱하기 때문입니다. 그것은 역시 때때로 신발끈 방법(shoelace method)이라고 불립니다. 그것은 다른 분야 중에서도 측량과 임업에서 응용을 가집니다.
그 공식은 1769년에 마이스터 알베르트 루드비히 프레드리히(Meister Albrecht Ludwig Friedrich (1724–1788)와 1795년에 카를 프리드리히 가우스(Carl Friedrich Gauss)에 의해 설명되었습니다. 그것은 다각형을 삼각형(triangle)으로 나눔으로써 검증될 수 있고, 그린의 정리(Green's theorem)의 특별한 경우로 여길 수 있습니다.
그 넓이 공식은 각 가장자리 AB를 취하고, 원점 O에 꼭짓점을 갖는 삼각형 ABO의 넓이를 계산하여, (평행사변형(parallelogram)의 넓이를 제공하는) 교차-곱을 취하고 2로 나눔으로써 유도됩니다. 우리가 다각형 주위를 감쌀 때, 양과 음의 넓이를 갖는 삼각형이 겹치질 것이고, 원점과 다각형 사이의 넓이는 취소되고 합해서 0이 될 것이지만, 오직 참조 삼각형 내부의 넓이가 남습니다. 이것이 측량자의 공식이라고 불리는 이유인데, 왜냐하면 "측량자"가 원점에 있기 때문입니다; 만약 반-시계-방향으로 가면, 양의 넓이가 왼쪽에서 오른쪽으로 갈 때 더해지고 음의 넓이가 오른쪽에서 왼쪽으로 갈 때 더합니다.
그 넓이 공식은 역시 자기-중첩하는 다각형에 적용될 수 있는데 왜냐하면 넓이의 의미는 심지어 자기-중첩하는 다각형이 일반적으로 단순(simple)이 아닐지라도 여전히 명확하기 때문입니다. 게다가, 자기-중첩하는 다각형은 여러 "해석"을 가질 수 있지만 신발끈 공식은 다각형의 공식이 해석에 상관없이 같음을 보이기 위해 사용될 수 있습니다.
Statement
그 공식은 다음 표현에 의해 설명될 수 있습니다:
\(\quad\displaystyle \begin{align} \mathbf{A} & = {1 \over 2} \left| \left(\sum_{i=1}^{n-1} x_iy_{i+1}\right) + x_ny_1 - \left(\sum_{i=1}^{n-1} x_{i+1}y_i\right) - x_1y_n \right| \\[4pt]
& = {1 \over 2}|x_1y_2 + x_2y_3 + \cdots + x_{n-1}y_n + x_n y_1 - x_2y_1 - x_3y_2 - \cdots - x_ny_{n-1} - x_1y_n| \end{align} \)
여기서
- A는 다각형의 넓이입니다,
- n은 다각형의 변의 개수입니다, 그리고
- \((x_i,y_i), i=1,2,...,n\)는 다각형의 순서화된 꼭짓점 (또는 "구석")입니다.
대안적으로
\(\quad\displaystyle
\begin{align}
\mathbf{A} & = {1 \over 2} \left| \sum_{i=1}^n x_i(y_{i+1}-y_{i-1}) \right| = {1 \over 2} \left| \sum_{i=1}^n y_i(x_{i+1}-x_{i-1}) \right| = {1 \over 2} \left| \sum_{i=1}^n (x_iy_{i+1}-x_{i+1}y_i) \right| \\[5pt]
& = {1 \over 2} \left| \sum_{i=1}^n (x_{i+1}+x_i)(y_{i+1}-y_i) \right| = {1 \over 2} \left| \sum_{i=1}^n \det\begin{pmatrix} x_i & x_{i+1} \\ y_i & y_{i+1} \end{pmatrix} \right|
\end{align}
\)
여기서 \(x_{n+1}=x_1\)와 \(x_0=x_n\)이고, 마찬가지로 \(y_{n+1}=y_1\)와 \(y_0=y_n\)입니다.
만약 점들이 반-시계방향에서 순차적으로 이름이 지정되면, 위의 행렬식(determinant)의 합이 양수이고 절댓값 기호는 생략될 수 있습니다; 만약 그것들이 시계 방향으로 이름이 지정되면, 행렬식의 합이 음수일 것입니다. 이것은 그 공식이 그린의 정리(Green's theorem)의 특별한 경우로 보일 수 있기 때문입니다.
공식의 특별하게 간결한 명제는 외부 대수(exterior algebra)의 관점에서 주어질 수 있습니다. 만약 \(\displaystyle v_1, \dots, v_n \)이 다각형의 연속적인 꼭짓점이면 (데카르트 평면에서 벡터로 여겨짐), 다음입니다:
\(\quad\displaystyle A = \frac{1}{2} \cdot \left| \sum_{i=1}^{n} v_i \wedge v_{i+1} \right|. \)
Proofs
Proof for a triangle
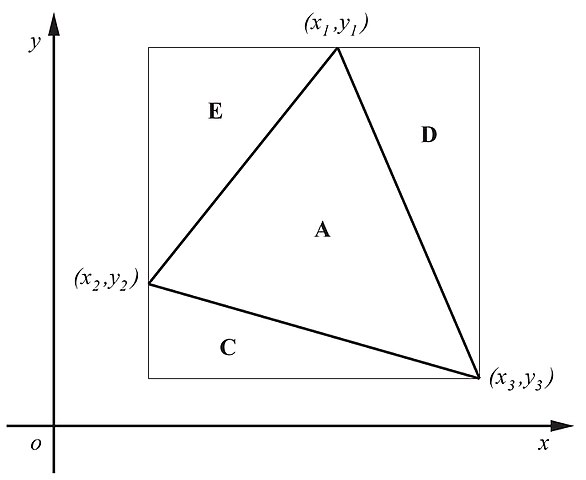
그림을 참조하여, \(\displaystyle \mathbf{A}\)를 그것의 꼭짓점이 좌표 \(\displaystyle (x_1,y_1), (x_2,y_2)\), 및 \(\displaystyle (x_3,y_3)\)에 의해 주어지는 삼각형의 넓이로 놓습니다. 삼각형 주위로 최소 넓이 직사각형을 그리므로 그것의 변은 \(\displaystyle x\) 또는 \(\displaystyle y\) 축에 평행합니다. 삼각형의 적어도 하나의 꼭짓점이 삼각형의 구석 위에 있을 것입니다. 그림에서, 삼각형을 둘러싸는 셋의 넓이는 \(\displaystyle \mathbf{C}, \mathbf{D}\), 및 \(\displaystyle \mathbf{E}\)입니다. 분명하게 \(\displaystyle \mathbf{A}\)는 직사각형의 넓이 (그것을 \(\displaystyle \mathbf{R}\)로 부름) 빼기 다른 셋의 삼각형의 넓이와 같습니다:
\(\quad\displaystyle \mathbf{A}=\mathbf{R}-\mathbf{C}-\mathbf{D}-\mathbf{E}\)
그림을 살펴보면 넓이가 다음에 의해 주어진다는 것을 알 수 있습니다:
\(\quad\displaystyle \mathbf{R}=(x_3-x_2)(y_1-y_3)=(x_3y_1+x_2y_3)-(x_3y_3+x_2y_1)\)
\(\quad\displaystyle -\mathbf{C}=-\frac{1}{2}(x_3-x_2)(y_2-y_3)=\frac{1}{2}(-x_3y_2-x_2y_3)+\frac{1}{2}(x_3y_3+x_2y_2)\)
\(\quad\displaystyle -\mathbf{D}=-\frac{1}{2}(x_3-x_1)(y_1-y_3)=\frac{1}{2}(-x_3y_1-x_1y_3)+\frac{1}{2}(x_3y_3+x_1y_1)\)
\(\quad\displaystyle -\mathbf{E}=-\frac{1}{2}(x_1-x_2)(y_1-y_2)=\frac{1}{2}(-x_1y_1-x_2y_2)+\frac{1}{2}(x_1y_2+x_2y_1)\)
항을 모우고 다시-배열하면 다음을 산출합니다:
\(\quad\displaystyle \mathbf{A}=\frac{1}{2}((x_2y_3-x_3y_2)-(x_1y_3-x_3y_1)+(x_1y_2-x_2y_1))\)
이것은 다음 행렬식으로 쓸 수 있습니다:
\(\quad\displaystyle \mathbf{A}=\frac{1}{2}\begin{vmatrix}1&1&1\\x_1&x_2&x_3\\y_1&y_2&y_3\end{vmatrix}\)
만약 좌표가 시계 순서로 쓰이면, 행렬식의 값은 \(\displaystyle -\mathbf{A}\)일 것입니다.
또 다른 방법으로 다시-정렬하면
\(\quad\displaystyle \mathbf{A}=\frac{1}{2}|x_1y_2+x_2y_3+x_3y_1-x_2y_1-x_3y_2-x_1y_3|\)
이것은 신발끈 공식의 형식입니다. 이 공식은 임의의 다각형의 넓이를 찾는 것으로 확장될 수 있는데 왜냐하면 단순 다각형은 삼각형으로 나뉠 수 있기 때문입니다.
Proof for a quadrilateral and general polygon

사변형의 넓이를 찾는 것은 다각형을 삼각형으로 나눔으로써 신발끈 공식이 임의의 다각형으로 일반화되는 방법을 시연합니다. 그것의 좌표가 반-시계 순서로 이름 붙여진 사변형의 그림을 생각해 보십시오. 사변형은 넓이 \(\displaystyle \mathbf{A}\)와 \(\displaystyle \mathbf{B}\)를 갖는 두 삼각형으로 나뉩니다. 각 삼각형에 대한 삼각형 공식을 사용하여 우리는 다음을 얻습니다:
\(\quad\displaystyle \mathbf{A}=\frac{1}{2}(x_1y_2+x_2y_3+x_3y_1-x_2y_1-x_3y_2-x_1y_3)\)
\(\quad\displaystyle \mathbf{B}=\frac{1}{2}(x_1y_3+x_3y_4+x_4y_1-x_3y_1-x_4y_3-x_1y_4)\)
삼각형 둘 다는 반-시계 방향으로 추적되었으므로, 넓이 둘 다는 양수이고 우리는 두 넓이를 더함으로써 사변형의 넓이를 얻습니다. \(\displaystyle \mathbf{A}\)의 마지막 양의 항과 마지막 음의 항은 \(\displaystyle \mathbf{B}\)의 첫 번째 양의 항과 첫 번째 음의 항과 취소되고 다음을 제공합니다:
\(\quad\displaystyle \mathbf{A}_\text{quad.}=\frac{1}{2}(x_1y_2+x_2y_3+x_3y_4+x_4y_1-x_2y_1-x_3y_2-x_4y_3-x_1y_4).\)
Examples
사용자는 데카르트 평면에서 다각형의 점들을 알아야 합니다. 예를 들어, 삼각형을 좌표 {(2, 1), (4, 5), (7, 8)}를 갖도록 취하십시오. 첫 번째 x-좌표를 취하고 그것을 두 번째 y-값과 곱하고, 그런-다음 두 번째 x-좌표를 취하고 그것을 세 번째 y-값과 곱하고, 모든 원했던 점에 대해 행해질 때까지 여러 번 반복하십시오. 이것은 다음 공식에 의해 각각의 좌표를 나타내는 \(x_i\)와 \(y_i\)에 대해 표현될 수 있습니다:
\(\quad\displaystyle \mathbf{A}_\text{tri.} = {1 \over 2}|x_1y_2 + x_2y_3 + x_3y_1 - x_2y_1 - x_3y_2 - x_1y_3|\)
이 공식은 단지 경우 n = 3에 대해 위에 주어진 공식의 확장입니다. 그것을 사용하여, 우리는 삼각형의 넓이가 10 + 32 + 7 − 4 − 35 − 16의 절댓값(absolute value)의 절반, 즉 3과 같다는 것을 알 수 있습니다. 변수의 숫자는 다각형(polygon)의 변의 숫자에 따라 달라집니다. 예를 들어, 오각형(pentagon)은 \(x_5\)와 \(y_5\)까지 정의될 것입니다:
\(\quad\displaystyle \mathbf{A}_\text{pent.} = {1 \over 2}|x_1y_2 + x_2y_3 + x_3y_4 + x_4y_5 + x_5y_1 - x_2y_1 - x_3y_2 - x_4y_3 - x_5y_4 - x_1y_5|\)
그리고 사변형(quadrilateral)은 \(x_4\)와 \(y_4\)까지 정의될 것입니다:
\(\quad\displaystyle \mathbf{A}_\text{quad.} = {1 \over 2}|x_1y_2 + x_2y_3 +x_3y_4 + x_4y_1 - x_2y_1 - x_3y_2 - x_4y_3 - x_1y_4|.\)
More complex example
점 (3, 4), (5, 11), (12, 8), (9, 5) 및 (5, 6)에 의해 정의된 다각형을 생각해 보십시오,
이 다각형의 넓이는 다음입니다:
\(\quad\displaystyle \begin{align}
\mathbf{A} & = {1 \over 2}\,\big|3 \times 11 + 5 \times 8 + 12 \times 5 + 9 \times 6 + 5 \times 4 \\
& {} \qquad {} - 4 \times 5 - 11 \times 12 - 8 \times 9 - 5 \times 5 - 6 \times 3\big| \\[10pt]
& = {60 \over 2} = 30.
\end{align}\)
Etymology

이 공식이 신발끈 공식이라고 불리는 이유는 그것을 평가하기 위해 사용되는 공통적인 방법이기 때문입니다. 이 방법은 행렬(matrices)을 사용합니다. 예제로서, 꼭짓점 (2, 4), (3, −8), 및 (1, 2)을 갖는 삼각형을 선택합니다. 그런-다음 삼각형을 "주위를 걷고" 시작점으로 끝남으로써 다음 행렬을 구성합니다.
\(\quad\displaystyle \begin{bmatrix} 2 & 4 \\ 3 & -8 \\ 1 & 2 \\ 2 & 4 \end{bmatrix}\)
먼저, (아래 그림과 같이) 대각선 아래쪽으로 오른쪽 슬래시를 그리십시오.

그리고 각 슬래시에 의해 연결된 두 숫자를 곱하고, 그런-다음 모든 곱을 더하십시오: (2 × −8) + (3 × 2) + (1 × 4) = −6. 대각선 아래쪽으로 왼쪽 슬래시로 같은 작업을 수행하십시오 (아래에 아래방향 슬래시로 표시됨):

(4 × 3) + (−8 × 1) + (2 × 2) = 8. 그런-다음 이들 두 숫자의 차이를 취하십시오: |(−6) − (8)| = 14. 이것을 반으로 나누면 삼각형의 넓이: 7을 제공합니다. 이것과 같은 숫자를 구성하면 공식을 더 쉽게 기억하고 평가할 수 있습니다. 모든 슬래시가 그려지면, 행렬은 끈이 다 묶인 신발과 느슨하게 닮아, 알고리듬의 이름을 불러일으킵니다.
See also
References
- Bart Braden (1986). "The Surveyor's Area Formula" (PDF). The College Mathematics Journal. 17 (4): 326–337. doi:10.2307/2686282. JSTOR 2686282.
- Dahlke, Karl. "Shoelace Formula". Retrieved 9 June 2008.
- Hans Pretzsch, Forest Dynamics, Growth and Yield: From Measurement to Model, Springer, 2009, ISBN 3-540-88306-1, p. 232.
- Meister, A. L. F. (1769), "Generalia de genesi figurarum planarum et inde pendentibus earum affectionibus", Nov. Com. Gött. (in Latin), 1: 144.
- P.W. Shor; C.J. Van Wyk (1992), "Detecting and decomposing self-overlapping curves", Comput. Geom. Theory Appl., 2 (1): 31–50, doi:10.1016/0925-7721(92)90019-O
- Ralph P. Boland; Jorge Urrutia (2000). Polygon Area Problems. 12th Canadian Conference on Computational Geometry. pp. 159–162.
- Shoelace Theorem, Art of Problem Solving Wiki.
- Weisstein, Eric W. "Polygon Area". Wolfram MathWorld. Retrieved 24 July 2012.
- Richard Rhoad; George Milauskas; Robert Whipple (1991). Geometry for Enjoyment and Challenge (new ed.). McDougal Littell. pp. 717–718. ISBN 0-86609-965-4.
- IMSA JHMC Guide, Page. 10 "Shoelace" by Cindy Xi
External links
