삼각함수에서, 그의 정의로부터 값을 평가하기 위해서, 적어도 2개의 변의 길이를 측정해야 하는 문제가 있습니다.
이런 문제를 극복하기 위해, 이미 알고 있는 삼각함수의 값으로부터 산술적 조작을 통해서 새로운 각의 삼각함수의 값을 평가하는 방법을 생각할 수 있습니다. 예를 들어, 우리가 잘 알고 있는 30°, 45°의 삼각함수의 값으로부터 더 각의 합, 75°, 또는 두 각의 차이, 15°의 삼각함수의 값을 평가할 수 있기를 원합니다.
이 과정의 결과물은 삼각함수의 덧셈정리(각도 합 항등식 및 각도 차 항등식)라고 불립니다.
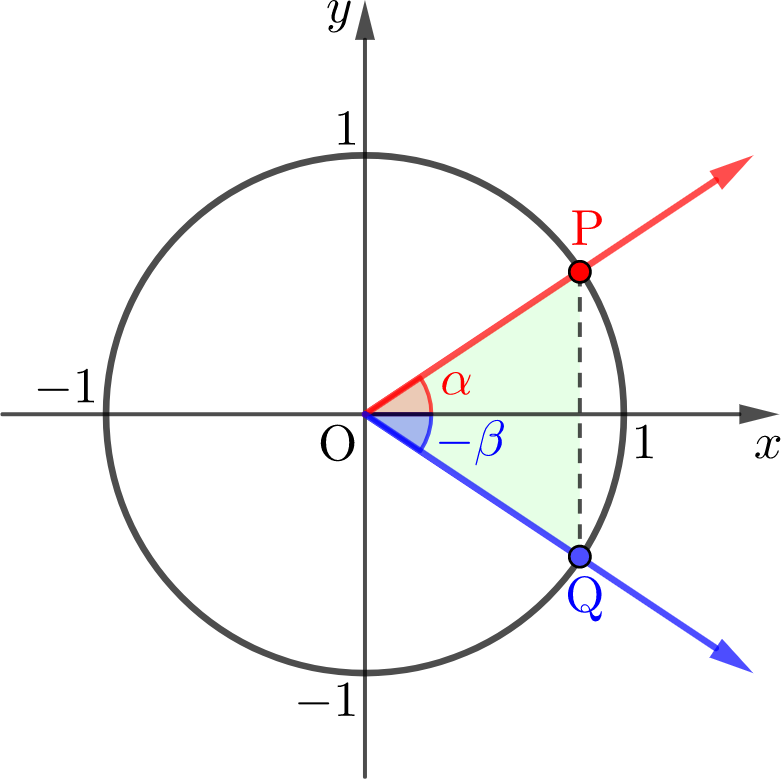
우리는 같은 원에서 중심각이 같으면, 그의 현의 길이가 서로 같음을 알고 있습니다. 그리고 그의 계산이 쉽게 되기 위해서, 적절한 위치에 동경을 두어야 합니다.
계산에서 가장 쉬운 동경의 위치는 (1,0)을 포함하는 위치입니다.
이때, 두 동경 \(\alpha, -\beta\)에 대해, 단위원 위의 표시된 두 점은 \(\mathrm{P}(\cos\alpha, \sin\alpha)\), \(\mathrm{Q}(\cos(-\beta), \sin(-\beta))\)로 놓습니다.
이때, 삼각함수의 변환에 따라, \(\cos(-\beta)=\cos\beta\), \(\sin(-\beta)=-\sin\beta\)이므로, 점 \(\mathrm{Q}\)는 \((\cos\beta, -\sin\beta)\)로 나타낼 수 있습니다.
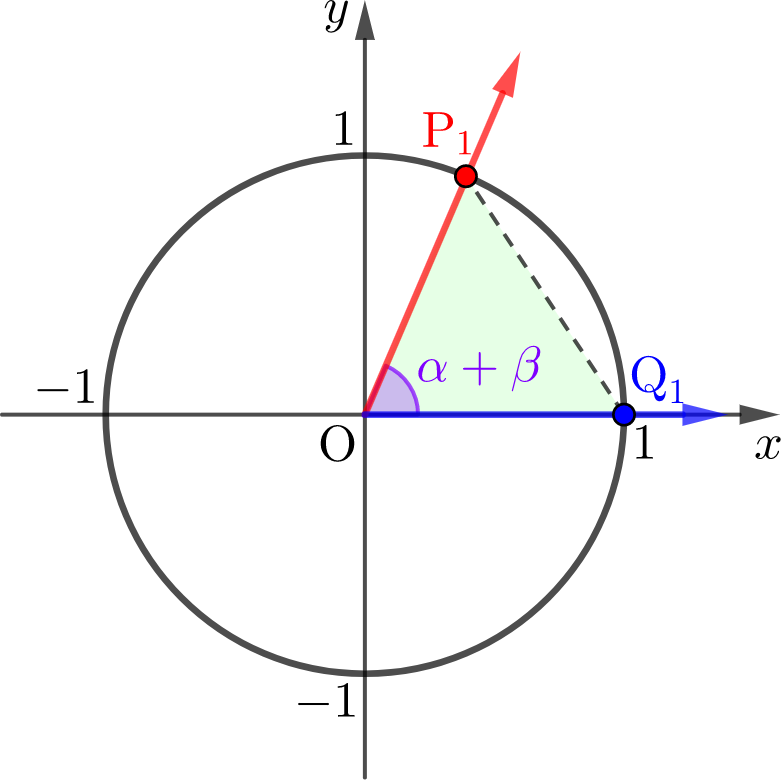
한편, 두 점 \(\mathrm{P}, \mathrm{Q}\)는 각각 원점을 중심으로 양의 방향으로 \(\beta\)만큼 회전한 후, \(\mathrm{P}_1, \mathrm{Q}_1\)에 놓이고, 두 점의 좌표는 \(\mathrm{P}_1(\cos(\alpha+\beta), \sin(\alpha+\beta))\), \(\mathrm{Q}_1(1, 0)\)으로 나타낼 수 있습니다.
따라서, 두 점 사이의 거리는
\(\quad\)\(\overline{\mathrm{PQ}}^2=(\cos\beta-\cos\alpha)^2+(-\sin\beta-\sin\alpha)^2\cdots(A)\)
\(\quad\)\(\overline{\mathrm{P_1Q_1}}^2=\left\{1-\cos(\alpha+\beta)\right\}^2+\sin^2(\alpha+\beta)\cdots(B)\)
이때, 두 점 \(\mathrm{P,Q}\)로 이루는 중심각과 \(\mathrm{P_1,Q_1}\)으로 이루는 중심각이 서로 같으므로, 두 점으로 이루는 현의 길이도 서로 같습니다.
따라서, 식 (A), (B)은 서로 같으므로, 전개해서 정리하면 (이때, 삼각함수 사이의 관계를 이용합니다), 삼각함수의 첫 번째 덧셈정리를 얻을 수 있습니다:
\(\quad\)\(\cos(\alpha+\beta)=\cos\alpha\cos\beta-\sin\alpha\sin\beta\cdots(1)\)
한편, 삼각함수의 변환에 의해, \(\sin\theta=\cos\left(\frac{\pi}{2}-\theta\right)\)이므로
\(\quad\)\(\begin{align}
\sin(\alpha+\beta) & = \cos \left\{ \frac{\pi}{2} - (\alpha + \beta) \right\} \\
& = \cos\left\{\left(\frac{\pi}{2}-\alpha\right)+(-\beta)\right\} \\
& = \cos\left(\frac{\pi}{2}-\alpha\right)\cos(-\beta)-\sin\left(\frac{\pi}{2}-\alpha\right)\sin(-\beta) \\
\end{align}\)
삼각함수의 변환에 의해 다음과 같이 두 번째 덧셈정리를 얻을 수 있습니다:
\(\quad\)\(\sin(\alpha+\beta)=\sin\alpha\cos\beta+\cos\alpha\sin\beta\cdots(2)\)
또한, 위의 두 결과로부터 \(\displaystyle \tan\theta=\frac{\sin\theta}{\cos\theta}\)이므로
\(\quad\)\(\displaystyle \tan(\alpha+\beta)=\frac{\sin(\alpha+\beta)}{\cos(\alpha+\beta)}=\frac{\sin\alpha\cos\beta+\cos\alpha\sin\beta}{\cos\alpha\cos\beta-\sin\alpha\sin\beta}\)
여기서, 분자, 분모를 각각 \(\cos\alpha\cos\beta(\cos\alpha\cos\beta\neq0)\)로 나누면
\(\quad\)\(\displaystyle \tan(\alpha+\beta)=\frac{\dfrac{\sin\alpha}{\cos\alpha}+\dfrac{\sin\beta}{\cos\beta}}{1-\dfrac{\sin\alpha\sin\beta}{\cos\alpha\cos\beta}}=\frac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta}\cdots(3)\)
한편, 식 (1),(2),(3)에 대해, \(\beta\) 대신에 \(-\beta\)를 각각 대입하면, 삼각함수의 변환에 의해, \(\sin(-\beta)=-\sin\beta\), \(\cos(-\beta)=\cos\beta\), \(\tan(-\beta)=-\tan\beta\)입니다.
따라서, 새로운 식 3개를 얻을 수 있습니다:
\(\quad\)\(\cos(\alpha-\beta)=\cos\alpha\cos\beta+\sin\alpha\sin\beta\cdots(4)\)
\(\quad\)\(\sin(\alpha-\beta)=\sin\alpha\cos\beta-\cos\alpha\sin\beta\cdots(5)\)
\(\quad\)\(\displaystyle \tan(\alpha-\beta)=\frac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta}\cdots(6)\)
삼각함수의 덧셈정리는 식 (1),(2),(3)을 가리키는 말입니다. 아래의 식 (4),(5),(6)은 변환으로 구할 수 있지만, 근본적으로 원래 식에 음의 값을 대입하는 것으로 생각해도 전혀 이상하지 않는데, 45°–30°를 45°+(–30°)로 사용하는 것은 항상 가능한 일입니다. 단지, 변환을 식에 적용해서 식을 암기할 것인지, 또는 숫자를 대입한 후에, 변환을 적용해서 구할지는 우리의 선택입니다.
다른 증명
여러 다른 증명 중에 Proofs_of_trigonometric_identities#Angle sum identities을 참조할 수 있으며, 보다 간편한 아래의 증명 방법도 있습니다.
사인, 코사인의 덧셈정리는 연결한 두 직각삼각형의 마지막 빗변의 길이를 1로 두고 가로와 세로의 길이를 정리한 것이며, 탄젠트의 덧셈정리는 길이 1의 인접변에서 두 직각삼각형으로 만들어진 빗변과 인접변과 나란한 윗변과 이루는 각도에 대해 탄젠트를 적용한 것입니다.
 |  |
두 직선의 사이의 예각
두 직선의 기울기 \(m_1, m_2\)라고 주어지면, \(m_1=\tan\alpha\), \(m_2=\tan\beta\)라고 놓으면, 두 직선 사이의 예각은 탄젠트의 덧셈정리로부터 구할 수 있습니다.
\(\quad\)\(\displaystyle \tan\theta=\left|\tan(\alpha-\beta)\right|=\left|\frac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta}\right|=\left|\frac{m_1-m_2}{1+m_1 m_2}\right|\)
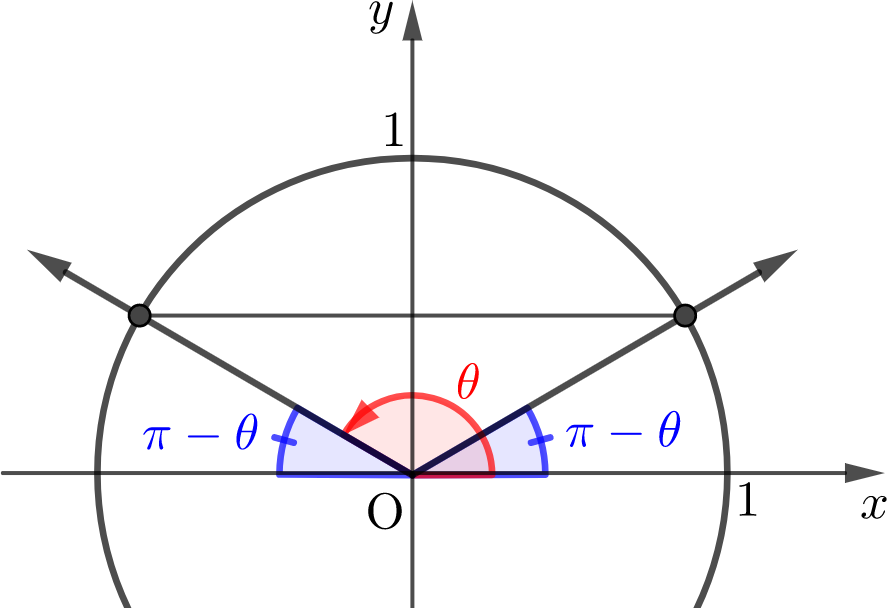
이때, 절댓값이 사용되는 이유는 만약 구한 값이 음수가 되어, 제 2사분면의 각 \(\left(\frac{\pi}{2}< \theta < \pi\right)\)이면, 두 직선의 예각은 \(\pi-\theta\)이고, 이 각의 탄젠트 값은
\(\quad\)\(\tan(\pi - \theta)= -\tan\theta\)
이고, 즉, 두 직선의 둔각의 절댓값과 예각의 절댓값은 서로 같으므로, 절댓값을 취하면, 제 2사분면의 각이 \(y\)-축 대칭으로 제 1사분면의 각으로 이동합니다. 이때, 제 1사분면 각(예각)은 절댓값을 취하더라도 부호가 바뀌지 않으므로, \(y\)-축 대칭으로 이동하지 않습니다.
대응하는 삼각함수의 값 구하기
만약 \(\sin\theta=\frac{1}{3}\)와 같이 하나의 삼각함수의 값을 알고 있을 때, 다른 삼각함수의 값을 구하는 방법에 대해 알아보고자 합니다.
물론, 삼각함수 사이의 관계를 통해, 주어진 값으로부터, 다른 삼각함수의 값의 평가를 대입해서 구할 수 있습니다.
| 삼각함수 사이의 값의 평가 | |||
| 주어진 값 | \(\sin \theta\) | \(\cos \theta\) | \(\tan \theta\) |
| \(\sin \theta = \) | \(\sin \theta\) | \(\pm \sqrt{1-\cos^2 \theta}\) | \(\displaystyle \pm \frac{\tan \theta}{\sqrt{1+\tan^2 \theta}}\) |
| \(\cos \theta = \) | \(\pm \sqrt{1-\sin^2 \theta}\) | \(\cos \theta\) | \(\displaystyle \pm \frac{1}{\sqrt{1+\tan^2 \theta}}\) |
| \(\tan \theta = \) | \(\displaystyle \pm \frac{\sin \theta}{\sqrt{1-\sin^2 \theta}}\) | \(\displaystyle \pm \frac{\sqrt{1-\cos^2 \theta}}{\cos \theta}\) | \(\tan \theta\) |
이런 공식까지 암기를 해야 하다면, 상당히 많은 항등식을 외워야 하는 새로운 문제가 생깁니다.
한편, 삼각함수의 특징을 이용해서, 하나의 삼각함수의 값으로부터 다른 삼각함수의 값을 구할 수 있습니다. 삼각함수는 길이비이기 때문에, 빗변을 특정 값으로 둘 이유는 없습니다.
어쨌든, 사인 값이 양수이므로 제 1,2사분면의 각일 수 있습니다. 이런 경우에서, 사분면의 위치를 알 수 없으므로, 코사인, 탄젠트의 값은 양수 또는 음수가 될 수 있습니다.
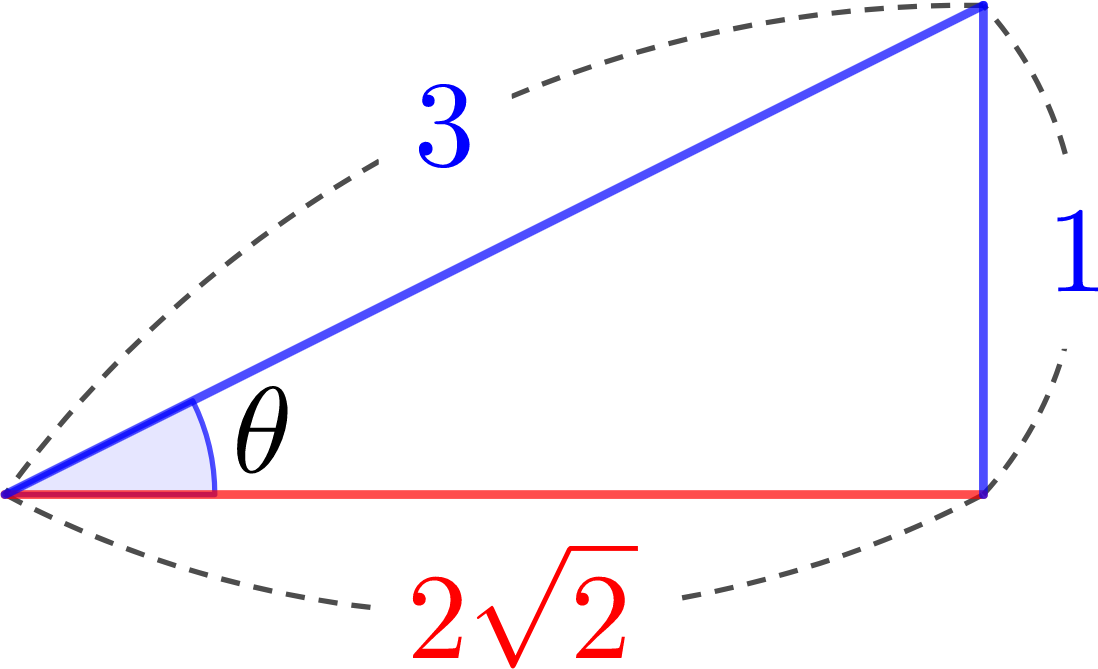
또한, 사인의 크기가 \(\frac{1}{3}\)이므로, 빗변의 길이를 \(3k\)라고 두면, 대변의 길이를 \(1k\)라고 놓을 수 있습니다.
그러므로, 직각삼각형에서, 나머지 변의 길이는, 피타고라스의 정리에 의해, \(2\sqrt{2}k\)로 구해집니다.
따라서,
\(\quad\)\(\displaystyle \cos\theta=\pm\frac{2\sqrt{2}}{3},\; \tan\theta=\pm\frac{1}{2\sqrt{2}}\)
여기서, \(k \ne 0\)이고, 삼각함수의 크기는 변의 길이의 비값이므로 \(k=1\)로 두고 생각해도 상관없습니다. 물론 임의의 유한한 실숫값을 선택할 수 있는데, 계산하기 가장 쉬운 값을 사용하는 것이 좋겠지요!!
그렇지만, \(\sin\theta=\frac{1}{3}\ \left(\frac{\pi}{2}<\theta<\pi\right)\)으로 주어진 경우에는, 제 2사분면의 각이므로, 부호가 하나로 결정되어, 다음과 같이 구해집니다:
\(\quad\)\(\displaystyle \cos\theta=-\frac{2\sqrt{2}}{3},\; \tan\theta=-\frac{1}{2\sqrt{2}}\)

