수학(mathematics)에서, 중복-집합(multiset)의 구성원의 중복도(multiplicity)는 중복-집합에 그것이 나타나는 횟수입니다. 예를 들어, 주어진 다항 방정식(polynomial equation)이 주어진 점에서 근(root)을 갖는 횟수는 해당 근의 중복도입니다.
중복도의 개념은 예외를 지정하지 않고 올바르게 세는 것이 가능하기 때문에 중요합니다 (예를 들어, 이중 근(double roots)은 두 번 셉니다). 그러므로 표현은, "중복도와 함께 셉니다".
만약 중복도가 무시되면, 이것은 "구별되는 근의 숫자"에서 처럼, 구별되는(distinct) 원소의 숫자를 세는 것으로써 강조될 수 있습니다. 어쨌든, (중복-집합과 대조적으로) 집합이 형성될 때마다, 중복도는, 용어 "구별되는"의 사용을 요구하지 않고, 자동으로 무시됩니다.
Multiplicity of a prime factor
소수 인수분해(prime factorization)에서, 예를 들어,
\(\quad\)60 = 2 × 2 × 3 × 5,
소수 인수 2의 중복도는 2이고, 반면에 소수 인수 3과 5 각각의 중복도는 1입니다. 따라서, 60은 중복도에 대해 허용하여 네 개의 소수 인수를 가지지만, 오직 세 개의 구별되는 소수 인수를 가집니다.
Multiplicity of a root of a polynomial
F를 필드(field)로 놓고 p(x)를 하나의 변수 및 F에서 계수를 갖는 다항식(polynomial)으로 놓습니다. 원소 a ∈ F는 만약 s(a) ≠ 0 및 \(p(x)=(x-a)^k s(x)\)를 만족하는 다항식 s(x)가 있으면, p(x)의 중복도 k의 근(root)입니다. 만약 k = 1이면, a는 단순 근(simple root)이라고 불립니다. 만약 k ≥ 2이면, a는 중복 근(multiple root)이라고 불립니다.
예를 들어, 다항식 \(p(x)=x^3+2x^2-7x+4\)는 근으로 1과 –4를 가지고, \(p(x)=(x+4)(x-1)^2\)으로 쓰일 수 있습니다. 이것은 1은 중복도 2의 근이고, 4는 (중복도 1의) '단순' 근임을 의미합니다. 근의 중복도는, 대수학의 기본 정리(fundamental theorem of algebra)에 의해, 다항식의 완전한 인수분해에서 이 근의 발생의 횟수입니다.
만약 a가 다항식의 중복도 k의 근이면, 그것은 그의 도함수(derivative)의 중복도 k – 1의 근입니다.
다항식의 판별식(discriminant)이 영인 것과 다항식이 중복 근을 가지는 것은 필요충분 조건입니다.
Behavior of a polynomial function near a multiple root
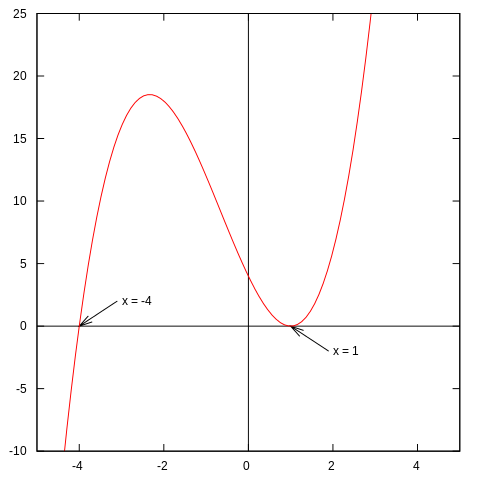
다항 함수(polynomial function) y = f(x)의 그래프(graph)는 다항식의 실수 근에서 x-축과 만납니다. 그래프는 f의 중복 근에서 이 축에 접하고(tangent) 단순 근에서 접하지 않습니다. 그래프는 홀수 중복도의 근에서 x-축을 가로지르고 짝수 중복도의 근에서 x-축에서 튕깁니다 (통과하지 않습니다).
비-영 다항 함수가 항상 비-음수(non-negative)인 것과 모든 그의 근이 짝수 중복도를 갖고 \(f(x_0) > 0\)를 만족하는 \(x_0\)가 존재하는 것은 필요충분 조건입니다.
Intersection multiplicity
대수 기하학(algebraic geometry)에서, 대수적 다양체의 두 부분-다양체의 교차는 기약 다양체(irreducible varieties)의 유한한 합입니다. 그러한 교차의 각 성분은 교차 중복도(intersection multiplicity)를 덧붙입니다. 이 개념은 이 성분의 임의의 일반적인 점(generic point)의 이웃에서 발생하는 것을 보고 정의될 수 있다는 의미에서 지역적(local)입니다. 그것은, 일반성을 잃지 않고, 우리가 고려할 수 있는, 교차 중복도를 정의하기 위해, 두 아핀 다양체(affines varieties) (아핀 공간의 부분-다양체)의 교차인 것을 따릅니다.
따라서, 두 아핀 다양체 \(V_1\)과 \(V_2\)가 주어지면, \(V_1\)과 \(V_2\)의 교차의 기약 성분(irreducible component) W를 생각해 보십시오. d를 W의 차원(dimension)으로 놓고, P를 W의 임의의 일반적인 점으로 놓습니다. P를 통과하는 일반적인 위치(general position)에서 d 초평면(hyperplane)과 W의 교차는 하나의 점 P로 감소되는 기약 성분을 가집니다. 그러므로, 교차의 좌표 링(coordinate ring)의 이 성분에서 지역 링(local ring)은 오직 하나의 소수 아이디얼(prime ideal)을 가지고, 그러므로 아르틴 링(Artinian ring)입니다. 이 링은 따라서 바닥 필드에 걸쳐 유한한 차원(finite dimensional) 벡터 공간입니다. 그의 차원은 W에서 \(V_1\)과 \(V_2\)의 교차 중복도(intersection multiplicity)입니다.
이 정의는 우리에게 베주의 정리(Bézout's theorem)와 정확하게 그의 일반화를 설명하는 것을 허용합니다.
이 정의는 다음 방법으로 다항식의 근의 중복도를 일반화합니다. 다항식 f의 근은 아핀 직선(affine line) 위의 점이며, 아핀 직선은 다항식에 의해 정의된 대수적 집합의 성분입니다. 이 아핀 집합의 좌표 링은 \(R=K[X]/\langle f\rangle\)이며, 여기서 K는 f의 계수를 포함하는 대수적으로 닫힌 필드(algebraically closed field)입니다. 만약 \(\displaystyle f(X)=\prod_{i=1}^k (X-\alpha_i)^{m_i}\)가 f의 인수분해이면, 소수 아이디얼 \(\langle X-\alpha_i\rangle\)에서 R의 지역 링은 \(K[X]/\langle (X-\alpha)^{m_i}\rangle\)입니다. 이것은 K에 걸쳐 벡터 공간으로, 그것은 차원으로 근의 중복도 \(m_i\)를 가집니다.
본질적으로 그의 책 Local Algebra에서 장-피에르 세르(Jean-Pierre Serre)로 기인한, 교차 중복도의 이 정의는, 내장된 성분(embedded components)에 대한 것이 아니라, 교차의 (역시 고립된 성분이라고 부르는) 집합 이론적 성분에 대해 오직 작동합니다. 이론은 내장된 경우를 다루는 것에 대해 개발되어 왔습니다 (자세한 것에 대해 교차 이론(Intersection theory)을 참조하십시오).
In complex analysis
\(z_0\)를 정칙 함수(holomorphic function) f의 근으로 놓고, n을 \(z_0\)에서 평가된 f의 n번째 도함수가 영과 다른 것을 만족하는 최소 양의 정수로 놓습니다. 그런 다음 \(z_0\)에 대한 f의 거듭제곱 급수는 n번째 항으로 시작하고, f는 중복도 (또는 “차수”) n의 근을 가지는 것으로 말합니다. 만약 n = 1이면, 근은 단순 근으로 불립니다.
우리는 유리형 함수의 영(zeroes)과 극(poles)의 중복도를 역시 정의할 수 있습니다. 따라서, 만약 우리가 유리형 함수 f = g/h를 가지면, 점 \(z_0\)에 대한 g와 h의 테일러 전개(Taylor expansions)를 취하고, (각각 항 m과 n의 차수를 나타내는) 각각에서 첫 번째 비-영 항을 찾으십시오. 만약 m = n이면, 점은 비-영 값을 가집니다. 만약 m < n이면, 점은 중복도 m − n의 하나의 영입니다. 만약 m < n이면, 점은 중복도 n − m의 하나의 극을 가집니다.
