본문 바로가기
영문 위키피디아 번역

(번역) Derivative

by 다움위키 2023. 11. 20.

실수 변수의 함수(function of a real variable)의 도함수(derivative)는 그의 인수 (입력 값)에서 변화에 관한 함숫값 (출력 값)의 변화에 대한 민감도를 측정합니다. 도함수는 미적분학(calculus)의 기본 도구입니다. 예를 들어, 시간(time)에 관한 움직이는 물체의 위치의 도함수는 물체의 속도(velocity)입니다: 이것은 시간이 경과할 때 물체의 위치가 얼마나 빨리 변하는지를 측정합니다.

선택된 입력 값에서 단일 변수의 함수의 도함수는, 그것이 존재할 때, 해당 점에서 함수의 그래프(graph of the function)에 대한 접선(tangent line)의 기울기(slope)입니다. 접선은 해당 입력 값 근처에서 함수의 최상의 선형 근사(linear approximation)입니다. 이 이유에 대해, 도함수는 종종 독립 변수의 변화에 대한 종속 변수에서 순간 변화의 비율, "순간 변화율(instantaneous rate of change)"로 묘사됩니다.

도함수는 여러 실수 변수의 함수(functions of several real variables)로 일반화될 수 있을 것입니다. 이 일반화에서, 도함수는 그의 그래프가 원래 함수의 그래프에 대한 (적절한 이동 후에) 최상의 선형 근사, 선형 변환(linear transformation)으로 다시-해석됩니다. 야코비 행렬(Jacobian matrix)은 독립 변수와 종속 변수의 선택에 의해 주어진 기저에 관한 이 선형 변환을 나타내는 행렬(matrix)입니다. 그것은 독립 변수에 관한 부분 도함수(partial derivative)의 관점에서 계산될 수 있습니다. 여러 변수의 실수-값 함수(real-valued function)에 대해, 야코비 행렬은 그래디언트 벡터(gradient vector)로 줄어듭니다.

도함수를 찾는 과정은 미분화(differentiation)로 불립니다. 반대 과정은 역미분화(antidifferentiation)로 불립니다. 미적분학의 기본 정리(fundamental theorem of calculus)는 역미분화를 적분화(integration)와 관련시킵니다. 미분화와 적분화는 단일-변수 미적분에서 두 가지 기본 연산을 구성합니다.

Differentiation

미분화(Differentiation)는 도함수를 계산하는 것의 행위입니다. 변수 x의 함수(function) y = f(x)의 도함수는 변수 x의 변화에 관한 함수의 값 y가 변하는 것에서 비율의 측정입니다. 그것은 x에 관한 f의 도함수(derivative)로 불립니다. 만약 x와 y가 실수(real number)이고, 만약 f의 그래프(graph)가 x에 대해 그려지면, 도함수는 각 점에서 이 그래프의 기울기(slope)입니다.

상수 함수(constant function)의 자명한 경우와는 별개로, 가장 단순한 경우는, y가 x의 선형 함수(linear function)인 경우이고, y의 그래프는 직선임을 의미합니다. 이 경우에서, 실수 m 및 b에 대해, y = f(x) = mx + b이고, 기울기 m은 다음으로 제공됩니다:

\(\quad\)\(\displaystyle m=\frac{\text{change in } y}{\text{change in } x} = \frac{\Delta y}{\Delta x},\)

여기서 기호 Δ (델타(Delta))는 "에서 변화"에 대해 약어이고, 조합 \(\Delta x\)와 \(\Delta y\)는 대응하는 변화, 즉: \(\Delta y = f(x + \Delta x)- f(x)\)를 참조합니다. 위 공식은 유지하는데, 왜냐하면 다음이기 때문입니다:

\(\quad\)\(\begin{align}
y + \Delta y &= f\left( x+\Delta x\right)\\
  &= m\left( x+\Delta x\right) +b =mx +m\Delta x +b \\
  &= y + m\Delta x.
\end{align} \)

따라서,

\(\quad\)\( \Delta y=m\Delta x. \)

이것은 직선의 기울기에 대한 값을 제공합니다.

만약 함수 f가 선형이 아니라면 (즉, 그의 그래프가 직선이 아니면), y에 대한 변화를 x에 대한 변화로 나눈 것은 고려된 범위에 걸쳐 변합니다: 미분화는, 특정 범위 \((\Delta x)\)를 가로지르는 것이 아니라, x의 임의의 주어진 값에서 변화의 이 비율에 대해 고유한 값을 찾기 위한 방법입니다.

그림에서 묘사된, 아이디어는 Δx가 무한히 작아질 때 차이의 비율(ratio of the differences) Δy / Δx의 극한 값(limit value)으로 변화의 비율을 계산하는 것입니다.

Notation

두 가지 구별되는 표기법이 도함수에 대해 공통적으로 사용되며, 하나는 라이프니츠(Leibniz)로부터 유래하고 다른 것은 조제프 루이 라그랑주(Joseph Louis Lagrange)로부터 유래합니다.

라이프니츠의 표기법(Leibniz's notation)에서, x에서 무한소(infinitesimal) 변화는 dx에 의해 표시되고, x에 관한 y의 도함수는 다음으로 쓰입니다:

\(\quad\displaystyle  \frac{dy}{dx}\)

이것은 두 무한소 양의 비율을 암시합니다. (위의 표현은 "x에 관한 y의 도함수", "dx에 의한 dy" 또는 "dx 위에 dy"로 읽힙니다. 구두 형식 "dy dx"는, 비록 그것이 혼동을 야기할지라도, 대화적으로 종종 사용됩니다.)

라그랑주의 표기법(Lagrange's notation)에서, 함수 f(x)의 x에 관한 도함수는 f'(x) ("x의 f 프라임"으로 읽음) 또는 \(f_x'(x)\) ("x의 f 프라임 x")으로 표시되고, 변수의 모호성의 경우에서 미분화에 의해 암시됩니다. 라그랑주의 표기법은 때때로 부정확하게 뉴턴(Newton)에 의해 발생한 것으로 여겨집니다.

Rigorous definition

이 직관적 아이디어를 정확한 정의로 바꾸는 가장 공통적인 접근법은 실수의 차이 몫의 극한(limit)으로 도함수를 정의하는 것입니다. 이것이 아래에 설명된 접근법입니다.

f를 실수 a의 열린 이웃(open neighborhood)에서 정의된 실수 값 함수로 놓습니다. 고전적인 기하학에서, a에서 함수 f의 그래프에 대한 접선은 f의 그래프를 가로-질러(transversally) 만나지 않는 점 (a, f(a))을 통과하는 유일한 직선이고, 이는 그 직선이 그래프를 일직선으로 통과하지 못한다는 것을 의미합니다. a에서 x에 관한 y의 도함수는, 기하학적으로, (a,에서 f의 그래프에 대한 접선의 기울기입니다. 접선의 기울기는 (a, f(a)) 및 그래프의 근처 점, 예를 들어 (a + h, f(a + h))을 통과하는 직선의 기울기에 매우 가깝습니다. 이들 직선은 가름선(secant line)으로 불립니다. h의 값이 영에 가까울수록 접선의 기울기에 대한 좋은 근사를 제공하고, h의 (절댓값(absolute value)에서) 더 작은 값은 일반적으로 더 좋은 근사(approximation)를 제공할 것입니다. 가름선의 기울기 m은 이들 점의 y 값들 사이의 차이는 x 값들 사이의 차이로 나눈 값이고, 즉, 다음입니다:

\(\quad\)\(\displaystyle m = \frac{\Delta f(a)}{\Delta a} = \frac{f(a+h)-f(a)}{(a+h)-(a)} = \frac{f(a+h)-f(a)}{h}.\)

이 표현은 뉴턴(Newton)의 차이 몫(difference quotient)입니다. 근사에서 정확한 답으로의 전달은 극한(limit)을 사용하여 행해집니다. 기하학적으로, 가름선의 극한은 접선입니다. 그러므로, h가 영에 접근할 때 차이 몫의 극한은, 만약 그것이 존재한다면, (a, f(a))에 대한 접선의 기울기를 반드시 나타내야 합니다. 이 극한은 a에서 함수 f의 도함수가 되는 것으로 정의됩니다:

\(\quad\)\(\displaystyle f'(a)=\lim_{h\to 0}\frac{f(a+h)-f(a)}{h}.\)

극한이 존재할 때, f는 a에서 미분-가능(differentiable)이라고 말합니다. 여기서 f′(a)는 도함수에 대해 여러 공통 표기법 중 하나입니다 (아래를 참조하십시오). 이 정의로부터 그것은, 미분-가능한 함수 f가 증가하는(increasing) 것과 그의 도함수가 양수인 것은 필요충분(iff) 조건이고 감소하는 것과 그의 도함수가 음수인 것은 필요충분 조건이라는 것은 분명합니다. 이 사실은 함수 행동을 분석할 때, 즉, 지역 극값(local extrema)을 찾을 때 확장적으로 사용됩니다.

동등하게, 도함수는 다음 속성을 만족시킵니다:

\(\quad\)\(\displaystyle \lim_{h\to 0}\frac{f(a+h) - (f(a) + f'(a)\cdot h)}{h} = 0,\)

이것은 a에서 f에 대한 접선이 a 근처의 (즉, 작은 h에 대해) f에 대한 최대 선형 근사(best linear approximation)를 제공한다는 직관적인 해석을 가집니다 (그림 1을 참조하십시오):

\(\quad\)\(f(a+h) \approx f(a) + f'(a)h\)

이 해석은 다른 설정에 일반화하는 것이 가장 쉬운 것입니다 (아래를 참조하십시오).

차이 몫에서 h에 대해 0으로 치환하는 것은 영에 의한 나눗셈(division by zero)에 기인하므로, 접선의 기울기는 이 방법을 사용하여 직접적으로 절대 찾을 수 없습니다. 대신에, h의 함수로 차이 몫이 되는 다음의 Q(h)를 정의하십시오:

\(\quad\)\(\displaystyle Q(h) = \frac{f(a + h) - f(a)}{h}.\)

Q(h)는 (a, f(a))와 (a + h, f(a + h)) 사이의 가름선의 기울기입니다. 만약 f가, 그의 그래프가 틈이 없는 깨지지-않은 곡선임을 의미하는, 연속 함수(continuous function)이면, Q는 h = 0에서 멀어지는 연속 함수입니다. 만약 극한 \(\lim_{h\to 0} Q(h)\)가 존재, Q를 연속 함수로 만드는 Q(0)에 대해 값을 선택할 수 있는 방법이 있다는 것을 의미하면, 함수 f는 a에서 미분 가능하고, a에서 그의 도함수는 Q(0)와 같습니다.

연습에서, h = 0에 대한 차이 몫 Q(h)의 연속 확장의 존재는 분모에서 h를 약분하기 위해 분자를 수정함으로써 보입니다. 그러한 조작은, 비록 Q가 h = 0에서 여전히 정의되지 않을지라도, 작은 h에 대해 Q의 극한 값을 만들 수 있습니다. 이 프로세스는 복잡한 함수에 대해 길고 지루할 수 있고, 많은 손쉬운 방법이 프로세스를 단순화하기 위해 공통적으로 사용됩니다.

Definition over the hyperreals

실수의 초실수(hyperreal) 확장 \(\mathbf{R} \subset \mathbf{^*R}\)에 상대적으로, 실수 점 x에서 실수 함수 y = f(x)의 도함수는 무한소(infinitesimal) ∆x에 대해 몫 \(\frac{\Delta y}{\Delta x}\)의 섀도우(shadow)로 정의될 수 있으며, 여기서 ∆y = f(x + ∆x) − f(x)입니다. 여기서 초실수에 대한 f의 자연스러운 확장은 여전히 f로 표시됩니다. 여기서 도함수는 만약 섀도우가 선택된 무한소와 독립이면 존재한다고 말합니다.

Example

\(f(x)=x^2\)에 의해 주어진 제곱 함수는 x = 3에서 미분-가능이고, 그곳에서 그의 도함수는 6입니다. 이 결과는 f(3)의 차이 몫의 h가 영에 가까워질 때 극한을 계산함으로써 수립됩니다:

\(\quad\)\(
\begin{align}
f'(3) & = \lim_{h\to 0}\frac{f(3+h)-f(3)}{h} = \lim_{h\to 0}\frac{(3+h)^2 - 3^2}{h} \\[10pt]
& = \lim_{h\to 0}\frac{9 + 6h + h^2 - 9}{h} = \lim_{h\to 0}\frac{6h + h^2}{h} = \lim_{h\to 0}{(6 + h)}.
\end{align}
\)

마지막 표현은 차이 몫이 h ≠ 0일 때 6 + h와 같고 h = 0일 때, 차이 몫의 정의 때문에, 정의되지 않음을 보여줍니다. 어쨌든, 극한의 정의는 h = 0일 때 차이 몫은 정의될 필요가 없다고 말합니다. 극한은 h가 영으로 가게 놓음으로써 결과이며, 그것이 h가 매우 작아지게 될 때 6 + h로 경향이 있는 값임을 의미합니다:

\(\quad\)\(\displaystyle  \lim_{h\to 0}{(6 + h)} = 6 + 0 = 6. \)

그러므로 점 (3, 9)에서 제곱 함수의 그래프의 기울기는 6이고, 그래서 x = 3에서 그의 도함수는 f′(3) = 6입니다.

보다 일반적으로, 비슷한 계산은 x = a에서 제곱 함수의 도함수가 f′(a) = 2a임을 보여줍니다:

\(\quad\)\(\begin{align}
f'(a) & = \lim_{h\to 0}\frac{f(a+h)-f(a)}{h} = \lim_{h\to 0}\frac{(a+h)^2 - a^2}{h} \\[0.3em]
& = \lim_{h\to 0}\frac{a^2 + 2ah + h^2 - a^2}{h} = \lim_{h\to 0}\frac{2ah + h^2}{h} \\[0.3em]
& = \lim_{h\to 0}{(2a + h)} = 2a
\end{align}\)

Continuity and differentiability

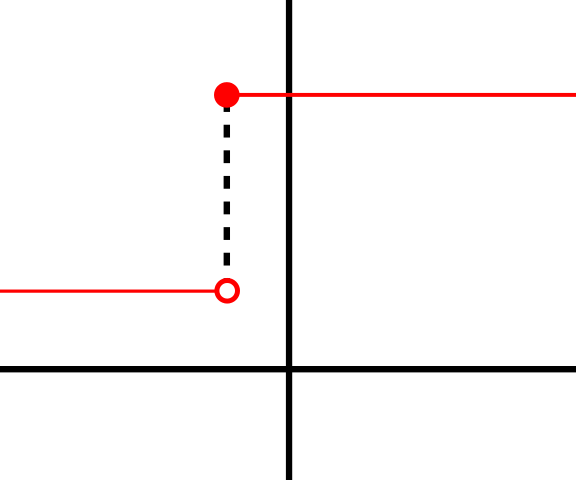
만약 f가 a에서 미분-가능(differentiable)이면, f는 역시 a에서 반드시 연속(continuous)입니다. 예제처럼, 점 a을 선택하고 f를 a보다 작은 모든 x에 대해 값 1을 반환하고, a보다 크거나 같은 모든 x에 대해 다른 값 10을 반환하는 계단 함수(step function)로 놓습니다. f는 a에서 도함수를 가질 수 없습니다. 만약 h가 음수이면, a + h가 단계의 낮은 부분에 있으므로, a에서 a + h까지 가름선은 매우 가파르고, h가 영으로 경향이 있을 때 기울기는 무한대로 경향이 있습니다. 만약 h가 양수이면, a + h가 단계의 상위 부분에 있으므로, a에서 a + h까지 가름선은 기울기 영을 가집니다. 결론적으로, 가름선은 임의의 단일 기울기에 접근하지 않으므로, 차이 몫의 극한은 존재하지 않습니다.

어쨌든, 심지어 함수가 한 점에서 연속일지라도, 그곳에서 미분-가능하지 않을 수 있을 것입니다. 예를 들어, f(x) = |x| 로 주어지는 절댓값 함수는 x = 0에서 연속이지만, 그곳에서 미분-가능하지 않습니다. 만약 h가 양수이면, 0에서 h까지 가름선의 기울기는 일이며, 반면에 만약 h가 음수이면, 0에서 h까지 가름선의 기울기는 음의 일입니다. 이것은 x = 0에서 그래프에서 "꼬임" 또는 "뾰족점"으로 그래픽으로 보일 수 있습니다. 심지어 매끄러운 그래프를 갖는 함수는 그의 접선이 수직(tangent is vertical)인 점에서 미분-가능이 아닙니다: 예를 들어, \(f(x)=x^{1/3}\)로 주어지는 함수는 x = 0에서 미분-가능이 아닙니다.

요약하면, 도함수를 가지는 함수는 연속이지만, 도함수를 가지지 않는 연속 함수가 있습니다.

연습에서 발생하는 대부분 함수는 모든 점 또는 거의 모든(almost every) 점에서 도함수를 가집니다. 미적분학의 역사 초기에서, 많은 수학자들은 연속 함수가 대부분의 점에서 미분-가능인 것으로 가정했습니다. 온화한 조건 아래에서, 예를 들어 만약 함수가 단조로운 함수(monotone function) 또는 립시츠 함수(Lipschitz function)이면, 이것은 참입니다. 어쨌든, 1872년 바이어슈트라스는 어디에서나 연속적이지만 어디에서도 미분-가능이 아닌 함수의 첫 번째 예제를 발견했습니다. 이 예제는 현재 바이어슈트라스 함수(Weierstrass function)로 알려져 있습니다. 1931년에, 스테판 바나흐(Stefan Banach)는 일부 점에서 도함수를 가지는 함수의 집합은 모든 연속 함수의 공간에서 마른 집합(meager set)이라는 것을 입증했습니다. 비공식적으로, 이것은 임의의 확률 연속 함수도 심지어 한 점에서 도함수를 가지지 않음을 의미합니다.

The derivative as a function

\(f\)를 그의 도메인(domain)에서 모든 각 점에서 도함수를 가지는 함수로 놓습니다. 우리는 그런-다음 모든 각 점 \(x\)를 \(x\)에서 \(f\)의 도함수의 값으로 매핑하는 함수로 정의할 수 있습니다. 이 함수는 \(f'\)로 쓰이고 \(f\)의 도함수 또는 도함수 함수로 불립니다.

때때로 f가 그의 도메인의 대부분이지만, 모두는 아닌 점에서 도함수를 가집니다. f′(a)가 정의되고 다른 곳에서 정의되지 않을 때마다, a에서 그의 값이 f′(a)인 함수는 f의 도함수로 역시 불립니다. 그것은 여전히 함수이지만, 그의 도메인은 f의 도메인보다 엄격하게 작습니다.

이 아이디어를 사용하여, 미분화는 함수의 함수가 됩니다: 도함수는, 그의 도메인이 그들 도메인의 모든 각 점에서 도함수를 가지는 모든 함수의 집합이고 그의 치역이 함수의 집합인 연산자입니다. 만약 우리가 이 연산자(operator)를 D로 표시하면, D(f)는 함수 f′입니다. D(f)는 함수이므로, 그것은 점 a에서 평가될 수 있습니다. 도함수 함수의 정의에 의해, D(f)(a) = f′(a)입니다.

비교에 대해, f(x) = 2x로 주어진 두 배 하는 함수를 생각해 보십시오; f는 실수의 실수-값 함수이며, 그것은 입력으로 숫자를 취하고 출력으로 숫자를 가진다는 의미입니다:

\(\quad\)\(\begin{align}
 1 &{}\mapsto 2,\\
 2 &{}\mapsto 4,\\
 3 &{}\mapsto 6.
\end{align}\)

연산자 D는, 어쨌든, 개별 숫자에서 정의되지 않습니다. 그것은 다음 함수 위에 오직 정의됩니다:

\(\quad\)\(\begin{align}
 D(x \mapsto 1) &= (x \mapsto 0),\\
 D(x \mapsto x) &= (x \mapsto 1),\\
 D\left(x \mapsto x^2\right) &= (x \mapsto 2\cdot x).
\end{align}\)

D의 출력이 함수이기 때문에, D의 출력은 한 점에서 평가될 수 있습니다. 예를 들어, D가 제곱 함수, x ↦ x2에 적용될 때, D는, 우리가 f(x)로 이름-지은, 두 배 하는 함수 x ↦ 2x를 출력합니다. 이 출력 함수는 그런-다음 f(1) = 2, f(2) = 4, 등등을 얻기 위해 평가될 수 있습니다.

Higher derivatives

f를 미분 가능 함수로 놓고, f ′를 그의 도함수로 놓습니다. f ′의 도함수는 (만약 그것이 하나를 가지면) f ′′로 쓰이고 f의 이차 도함수(second derivative of f)로 불립니다. 비슷하게, 이차 도함수의 도함수는, 만약 그것이 존재하면, f ′′′로 쓰이고, f의 삼차 도함수(third derivative of f)로 불립니다. 이 과정을 계속하면, 우리는, 만약 그것이 존재하면, n번째 도함수를 (n-1)번째 도함수의 도함수로 정의할 수 있습니다. 이들 반복된 도함수는 고차 도함수(higher-order derivatives)로 불립니다. n번째 도함수는 차수 n의 도함수(derivative of order n)로 역시 불립니다.

만약 x(t)가 시간 t에서 대상의 위치를 나타내면, x의 고차 도함수는 물리학(physics)에서 특성 해석을 가집니다. x의 일차 도함수는 물체의 속도(velocity)입니다. x의 이차 도함수는 가속도(acceleration)입니다. x의 삼차 도함수는 저크(jerk:가가속도)입니다. 그리고 마지막으로, x의 사차 도함수는 자운스(jounce:가가가속도)로 정의됩니다.

함수 f는, (예를 들어, 만약 그것이 연속이 아니면), 도함수를 가질 필요가 없습니다. 비슷하게, 비록 f가 도함수를 가질지라도, 이차 도함수를 갖지 않을 수 있을 것입니다. 예를 들어, 다음을 놓습니다:

\(\quad\)\(f(x) = \begin{cases} +x^2, & \text{if }x\ge 0 \\ -x^2, & \text{if }x \le 0.\end{cases}\)

계산은 \(x\)에서 그의 도함수가 다음으로 제공되는 미분-가능한 함수임을 보여줍니다:

\(\quad\)\(f'(x) = \begin{cases} +2x, & \text{if }x\ge 0 \\ -2x, & \text{if }x \le 0.\end{cases}\)

f'(x)는 \(x\)에서 두 배 절댓값 함수이고, 그것은 영에서 도함수를 갖지 않습니다. 비슷한 예제는 함수가 각 비-음의 정수 k에 대해 k번째 도함수를 가지지만 (k + 1)번째 도함수를 가지지 않음을 보여줍니다. k 연속적인 도함수를 가지는 함수는 k번 미분-가능(k times differentiable)으로 불립니다. 만약 게다가 k번째 도함수가 연속이면, 그 함수는 미분가능성 클래스(differentiability class) \(C^k\)가 된다고 말합니다. (이것은, Smoothness § Examples의 두 번째 예제에서 보인 것처럼, k 도함수를 가지는 것보다 더 강한 조건입니다.) 무한히 많은 도함수를 가지는 함수는 무한히 미분-가능(infinitely differentiable) 또는 매끄러운(smooth) 것으로 불립니다.

실수 직선 위에, 모든 각 다항 함수(polynomial function)는 무한히 미분-가능입니다. 표준 미분화 규칙(differentiation rules)에 의해, 만약 차수 n의 다항식이 n번 미분되면, 그것은 상수 함수(constant function)가 됩니다. 그의 후속 도함수의 모두는 동일하게 영입니다. 특히, 그것들은 존재하므로, 다항식은 매끄러운 함수입니다.

점 x에서 함수 f의 도함수는 x에 가까운 해당 함수에 대한 다항식 근사를 제공합니다. 예를 들어, 만약 f가 두 번 미분-가능이면,

\(\quad\)\( f(x+h) \approx f(x) + f'(x)h + \tfrac{1}{2} f''(x) h^2\)

그 의미에서 다음입니다:

\(\quad\)\(\displaystyle  \lim_{h\to 0}\frac{f(x+h) - f(x) - f'(x)h - \frac{1}{2} f''(x) h^2}{h^2}=0.\)

만약 f가 무한히 미분-가능이면, 이것은 x 주위의 x + h에서 평가된 f에 대해 테일러 급수(Taylor series)의 시작입니다.

Inflection point

함수의 이차 도함수가 부호를 변경하는 점은 변곡점(inflection point)으로 불립니다. 변곡점에서, \(f(x) = x^3\)으로 주어진 함수의 변곡점 x = 0의 경우에서 처럼, 이차 도함수는 영일 수 있을 것이며, 또는 \(f(x) = x^\frac{1}{3}\)으로 주어진 함수의 변곡점 x = 0의 경우에서 처럼, 그것은 존재에서 실패할 수 있을 것입니다. 변곡점에서, 함수는 볼록 함수(convex function)인 것에서 오목 함수(concave function)인 것으로 또는 그 반대로 바뀝니다.

Notation (details)

Leibniz's notation

기호 \(dx\), \(dy\), 및 \(\displaystyle \frac{dy}{dx}\)는 1675년에 고트프리트 빌헬름 라이프니츠(Gottfried Wilhelm Leibniz)에 의해 도입되었습니다. 그것은 방정식 y = f(x)가 종속 변수와 독립 변수 사이의 함수형 관계로 보일 때 여전히 공통적으로 사용됩니다. 그런-다음 일차 도함수는 다음으로 표시됩니다:

\(\quad\)\(\displaystyle \frac{dy}{dx},\quad\frac{d f}{dx}, \text{  or  }\frac{d}{dx}f,\)

및 한때 무한소(infinitesimal) 몫으로 생각되었습니다. 더 높은 도함수는 표기법을 사용하여, \(y = f(x)\)의 n번째 도함수에 대해, 다음으로 표현됩니다:

\(\quad\)\(\displaystyle \frac{d^ny}{dx^n},
\quad\frac{d^n f}{dx^n},
\text{  or  }
\frac{d^n}{dx^n}f\)

이것들은 도함수 연산자의 다양한 응용에 대해 약어입니다. 예를 들어,

\(\quad\)\(\displaystyle \frac{d^2y}{dx^2} = \frac{d}{dx}\left(\frac{dy}{dx}\right).\)

라이프니츠의 표기법과 함께, 우리는 점 \(x = a\)에서 \(y\)의 도함수를 두 다른 방법으로 쓸 수 있습니다:

\(\quad\)\(\displaystyle \left.\frac{dy}{dx}\right|_{x=a} = \frac{dy}{dx}(a).\)

라이프니츠의 표기법은 미분화에 대해 변수를 (분모에서) 지정하는 것을 허용하며, 이것은 부분 미분화(partial differentiation)와 관련됩니다. 그것은 역시 기억하기 위해 더 쉬운 체인 규칙(chain rule)을 만듭니다:

\(\quad\)\(\displaystyle \frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx}.\)

Lagrange's notation

때때로 프라임 표기법(prime notation)으로 언급되는, 미분화에 대해 가장 공통적인 현대 표기법 중 하나는 조제-프루이 라그랑주(Joseph-Louis Lagrange) 기인하고, 함수 \(f\)의 도함수는 \(f'\)으로 표시되도록, 프라임 표식(prime mark)을 사용합니다. 비슷하게, 이차 및 삼차 도함수는 다음으로 표시됩니다:

\(\quad\)\((f')'=f''\) 및 \((f'')'=f'''.\)

이 점을 벗어난 도함수의 숫자를 나타내기 위해, 일부 저자는 위첨자(superscript)에서 로마 숫자 시스템을 사용하지만, 다른 저자들은 괄호 안에 숫자를 넣습니다:

\(\quad\)\(f^{\mathrm{iv}}\) 또는 \(f^{(4)}.\)

후자 표기법은 \(f\)의 n번째 도함수에 대해 표기법 \(f^{(n)}\)을 산출하기 위해 일반화합니다 – 이 표기법은 우리가 함수 자체로서 도함수에 대해 이야기하기를 원할 때 가장 유용한데, 왜냐하면 이 경우에서 라이프니츠 표기법이 번거로울 수 있기 때문입니다.

Newton's notation

미분화에 대해, 역시 점 표기법으로 불리는, 뉴턴의 표기법(Newton's notation)은 시간 도함수를 나타내기 위해 함수 이름 위에 점을 위치시킵니다. 만약 \(y = f(t)\)이면,

\(\quad\)\(\dot{y}\) 및 \(\ddot{y}\)

은, 각각, \(y\)의 일차 및 이차 도함수를 나타냅니다. 이 표기법은 시간 또는 호 길이(arc length)에 관한 도함수에 대해 독점적으로 사용됩니다. 그것은 물리학(physics) 및 미분 기하학(differential geometry)의 미분 방정식(differential equation)에서 전형적으로 사용됩니다. 점 표기법은, 어쨌든, 고차 도함수 (4차 이상)에 대해 관리하기가 어렵게 되고, 다중 독립 변수를 다룰 수 없습니다.

Euler's notation

오일러(Euler)의 표기법은 미분 연산자(differential operator) \(D\)를 사용하며, 이것은 함수 \(f\)에 일차 도함수 \(Df\)를 제공하기 위해 적용됩니다. n번째 도함수는 \(D^nf\)로 표시됩니다.

만약 y = f(x)가 종속 변수이면, 종종 아래첨자 x가 독립 변수 x를 명확하게 하기 위해 D에 첨부됩니다. 오일러의 표기법은 그런-다음 다음으로 쓰입니다:

\(\quad\)\(D_x y\) 또는 \(D_x f(x)\),

비록 이 아래첨자가, 변수 x가 이해될 때, 예를 들어 이것이 표현에서 유일한 독립 변수일 때, 종종 생략됩니다.

오일러의 표기법은 선형 미분 방정식(linear differential equation)을 설명하고 해결하는 것에 유용합니다.

Rules of computation

함수의 도함수는, 원칙적으로, 차이 몫을 고려하고, 그의 극한을 계산함으로써 정의로부터 계산될 수 있습니다. 연습에서, 한번 몇 가지 간단한 함수의 도함수가 알려지면, 다른 함수의 도함수는 더 간단한 함수로부터 더 복잡한 함수의 도함수를 얻기 위한 규칙을 사용하여 더 쉽게 계산됩니다.

Rules for basic functions

대부분의 도함수 계산은 결국 일부 공통 함수의 도함수를 취하는 것을 요구합니다. 다음의 불완전한 목록은 단일 실수 변수와 그 도함수의 가장 자주 사용되는 함수 중 일부를 제공합니다.

i) 거듭제곱의 도함수(Derivatives of powers): 만약

\(\quad\)\( f(x) = x^r,\)

여기서 r은 임의의 실수이며, 이것이 정의되는 어디든지, 다음입니다:

\(\quad\)\( f'(x) = rx^{r-1}\).

예를 들어, 만약 \(f(x) = x^{1/4}\)이면,

\(\quad\)\(f'(x) = (1/4)x^{-3/4},\)

및 도함수 함수는 오직 양의 x에 대해 정의되고, x = 0에 대해 정의되지 않습니다. r = 0일 때, 이 규칙은, f′(x)가 x ≠ 0에 대해 영이라는 것을 암시하며, 이것은 거의 상수 규칙입니다 (아래에서 설명합니다).

ii) 지수(Exponential) 및 로그(logarithmic) 함수:

\(\quad\)\(\displaystyle  \frac{d}{dx}e^x = e^x.\)

\(\quad\)\(\displaystyle  \frac{d}{dx}a^x = a^x\ln(a).\)

\(\quad\)\(\displaystyle  \frac{d}{dx}\ln(x) = \frac{1}{x},\qquad x > 0.\)

\(\quad\)\(\displaystyle  \frac{d}{dx}\log_a(x) = \frac{1}{x\ln(a)}.\)

iii) 삼각 함수:

\(\quad\)\(\displaystyle  \frac{d}{dx}\sin(x) = \cos(x).\)

\(\quad\)\(\displaystyle  \frac{d}{dx}\cos(x) = -\sin(x).\)

\(\quad\)\(\displaystyle  \frac{d}{dx}\tan(x) = \sec^2(x) = \frac{1}{\cos^2(x)} = 1+\tan^2(x).\)

iv) 역 삼각 함수:

\(\quad\)\(\displaystyle  \frac{d}{dx}\arcsin(x) = \frac{1}{\sqrt{1-x^2}},\qquad -1<x<1.\)

\(\quad\)\(\displaystyle  \frac{d}{dx}\arccos(x)= -\frac{1}{\sqrt{1-x^2}},\qquad -1<x<1.\)

\(\quad\)\(\displaystyle  \frac{d}{dx}\arctan(x)= \frac{1}{{1+x^2}}\)

Rules for combined functions

많은 경우에서, 뉴턴의 차이 몫의 직접 응용에 의해 복잡한 극한 계산은 미분화 규칙을 사용하여 피해질 수 있습니다. 가장 기본적인 규칙 중 일부는 다음입니다.

i) 상수 규칙(Constant rule): 만약 f(x)은 상수이면,

\(\quad\)\(f'(x) = 0. \)

ii) 합 규칙(Sum rule):

\(\quad\)\((\alpha f + \beta g)' = \alpha f' + \beta g' \) 모든 함수 f와 g 및 모든 실수 \(\alpha\)와 \(\beta\)에 대해.

iii) 곱 규칙(product rule):

\(\quad\)\((fg)' = f 'g + fg' \) 모든 함수 f 및 g에 대해. 특수한 경우로, 이 규칙은 상수 규칙에 의해 \(\alpha' f = 0 \cdot f = 0\)때문에, \(\alpha\)가 상수일 때마다 사실 \((\alpha f)' = \alpha f'\)를 포함합니다.

iv) 몫 규칙(quotient rule):

\(\quad\)\(\left(\frac{f}{g} \right)' = \frac{f'g - fg'}{g^2}\) g ≠ 0인 모든 입력에서 모든 함수 f 및 g에 대해.

v) 체인 규칙(chain rule) 합성 함수에 대해: 만약 f ( x ) = h ( g ( x ) ) 이면,

\(\quad\)\(f'(x) = h'(g(x)) \cdot g'(x). \)

Computation example

다음 함수

\(\quad\)\(f(x) = x^4 + \sin \left(x^2\right) - \ln(x) e^x + 7\)

의 도함수는 다음입니다:

\(\quad\)\(
\begin{align}
f'(x) &= 4 x^{(4-1)}+ \frac{d\left(x^2\right)}{dx}\cos \left(x^2\right) - \frac{d\left(\ln {x}\right)}{dx} e^x - \ln(x) \frac{d\left(e^x\right)}{dx} + 0 \\
      &= 4x^3 + 2x\cos \left(x^2\right) - \frac{1}{x} e^x - \ln(x) e^x.
\end{align}
\)

여기서 두 번째 항은 체인 규칙(chain rule)을 사용하고 세 번째 항은 곱 규칙(product rule)을 사용하여 계산되었습니다. 기본 함수 \(x^2\), \(x^4\), \(\sin(x)\), 및 \(exp(x)=e^x\)의 알려진 도함수, 마찬가지로 상수 7이 역시 사용되었습니다.

In higher dimensions

Vector-valued functions

실수 변수의 벡터-값 함수(vector-valued function) y는 실수를 일부 벡터 공간(vector space) \(\mathbf{R}^n\)에서 벡터로 보냅니다. 벡터-값 함수는, \(\mathbf{y}(t)=(y_1(t),\cdots, y_2(t))\)임을 의미하는, 그의 좌표 함수 \(y_1(t), y_2(t), \cdots, y_n(t)\)로 나눌 수 있습니다. 이것은, 예를 들어, \(\mathbf{R}^2\) 또는 \(\mathbf{R}^3\)에서 매개-변수 곡선(parametric curve)을 포함합니다. 좌표 함수는 실수 값 함수이므로, 도함수의 위의 정의가 그들에게 적용됩니다. \(\mathbf{y}(t)\)의 도함수는, 접 벡터(tangent vector)로 불리는, 벡터(vector)가 되는 것으로 정의되며, 그의 좌표는 좌표 함수의 도함수입니다. 즉,

\(\quad\)\(\mathbf{y}'(t) = (y'_1(t), \ldots, y'_n(t)).\)

동등하게, 만약 극한이 존재하면,

\(\quad\)\(\displaystyle \mathbf{y}'(t)=\lim_{h\to 0}\frac{\mathbf{y}(t+h) - \mathbf{y}(t)}{h},\)

분자에서 뺄셈은, 스칼라가 아닌, 벡터의 뺄셈입니다. 만약 y의 도함수가 t의 모든 각 값에 대해 존재하면, y′은 또 다른 벡터-값 함수입니다.

만약 \(\mathbf{e}_1, \cdots, \mathbf{e}_n\)은 \(\mathbf{R}^n\)에 대해 표준 기저이면, y(t)는 \(y_1(t) \mathbf{e}_1 + \cdots + y_n(t) \mathbf{e}_n\)으로 역시 쓰일 수 있습니다. 만약 우리가, 벡터-값 함수의 도함수가 선형성(linearity) 속성을 유지함을 가정하면, y(t)의 도함수는 반드시 다음이어야 합니다:

\(\quad\)\(y'_1(t)\mathbf{e}_1 + \cdots + y'_n(t)\mathbf{e}_n\)

왜냐하면 기저 벡터의 각각은 상수입니다.

이 일반화는 유용하며, 예를 들어, 만약 y(t)가 시간 t에서 입자의 위치 벡터이면; 도함수 y′(t)는 시간 t에서 입자의 속도(velocity) 벡터입니다.

Partial derivatives

f가 둘 이상의 변수에 의존하는 함수라고 가정합니다—예를 들어,

\(\quad\)\(f(x,y) = x^2 + xy + y^2.\)

f는 다른 나머지 변수에 의해 인덱스되는 하나의 변수의 함수의 가족으로 재해석될 수 있습니다:

\(\quad\)\(f(x,y) = f_x(y) = x^2 + xy + y^2.\)

달리 말해서, x의 모든 각 값은, 하나의 실수의 함수인, \(f_x\)로 표시되는, 함수를 선택합니다. 즉,

\(\quad\)\(x \mapsto f_x,\)

\(\quad\)\(f_x(y) = x^2 + xy + y^2.\)

한번 x의 값이 선택되면, a라면, f(x, y)는 y를 \(a^2+ay+y^2\)로 보내는 함수 \(f_a\)를 결정합니다:

\(\quad\)\(f_a(y) = a^2 + ay + y^2.\)

이 표현에서, a는 변수가 아닌 상수이므로, \(f_a\)는 오직 하나의 실수 변수의 함수입니다. 결과적으로, 한 변수의 함수에 대해 도함수의 정의가 적용됩니다:

\(\quad\)\(f_a'(y) = a + 2y.\)

위의 절차는 a의 임의의 선택에 대해 수행될 수 있습니다. 도함수를 함수와 함께 모으는 것은 y 방향에서 f의 변화를 설명하는 함수를 제공합니다:

\(\quad\)\(\frac{\partial f}{\partial y}(x,y) = x + 2y.\)

이것은 y에 관한 f의 부분 도함수입니다. 여기서 ∂는 부분 도함수 기호(partial derivative symbol)로 불리는 둥근 d입니다. 문자 d로부터 그것을 구별하기 위해, ∂는 때때로 "dee" 대신에 "der", "del", 또는 "partial"로 발음됩니다.

일반적으로, 점 \((a_1,\cdots,a_n)\)에서 방향 \(x_i\)에서 함수 \(f(x_1,\cdots,x_n)\)의 부분 도함수(partial derivative)는 다음으로 정의됩니다:

\(\quad\)\(\displaystyle \frac{\partial f}{\partial x_i}(a_1,\ldots,a_n) = \lim_{h \to 0}\frac{f(a_1,\ldots,a_i+h,\ldots,a_n) - f(a_1,\ldots,a_i,\ldots,a_n)}{h}.\)

위의 차이 몫에서, \(x_i\)를 제외한 모든 변수는 고정되게 유지됩니다. 고정 값의 해당 선택은 하나의 변수의 함수를 결정합니다:

\(\quad\)\(f_{a_1,\ldots,a_{i-1},a_{i+1},\ldots,a_n}(x_i) = f(a_1,\ldots,a_{i-1},x_i,a_{i+1},\ldots,a_n),\)

그리고, 정의에 의해,

\(\quad\)\(\displaystyle \frac{df_{a_1,\ldots,a_{i-1},a_{i+1},\ldots,a_n}}{dx_i}(a_i) = \frac{\partial f}{\partial x_i}(a_1,\ldots,a_n).\)

달리 말해서, a의 다른 선택은 바로 위의 예제에서 처럼 일-변수 함수의 가족을 인덱스합니다. 이 표현은 부분 도함수의 계산이 일-변수 도함수의 계산으로 줄어음을 역시 보입니다.

여러 변수의 함수의 중요한 예제는 유클리드 공간 \(\mathbf{R}^n\) (예를 들어, \(\mathbf{R}^2\) 또는 \(\mathbf{R}^3\) 위에서)에서 도메인 위에 스칼라-값 함수(scalar-valued function) \(f(x_1,\cdots,x_n)\)의 경우입니다. 이 경우에서, f는 각 변수 \(x_j\)에 관한 부분 도함수 \(\partial f/\partial x_j\)를 가집니다. 점 \(a_1,\cdots,a_n)\)에서, 이들 부분 도함수는 다음 벡터를 정의합니다:

\(\quad\)\(\displaystyle \nabla f(a_1, \ldots, a_n) = \left(\frac{\partial f}{\partial x_1}(a_1, \ldots, a_n), \ldots, \frac{\partial f}{\partial x_n}(a_1, \ldots, a_n)\right).\)

이 벡터는 a에서 f의 그래디언트(gradient)로 불립니다. 만약 f가 일부 도메인의 모든 각 점에서 미분-가능이면, 그레디언트는 점 \(a_1,\cdots,a_n)\)을 벡터 \(\nabla f(a_1,\cdots,a_n)\)로 취하는 벡터-값 함수 ∇f입니다. 결과적으로, 그래디언트는 벡터 필드(vector field)를 결정합니다.

Directional derivatives

만약 f가 \(\mathbf{R}^n\) 위에 실수-값 함수이면, f의 부분 도함수는 좌표 축의 방향에서 그의 변화를 측정합니다. 예를 들어, 만약 f가 x와 y의 함수이면, 그의 부분 도함수는 x 방향과 y 방향에서 f 안의 변화를 측정합니다. 그들은, 어쨌든, 대각선 y = x를 따르는 것과 같은, 임의의 다른 방향에서 f의 변화를 직접 측정하지는 않습니다. 이것들은 방향 도함수를 사용하여 측정됩니다. 다음 벡터를 선택하십시오:

\(\quad\)\(\mathbf{v} = (v_1,\ldots,v_n).\)

점 x에서 v의 방향에서 f의 방향 도함수(directional derivative)는 다음 극한입니다:

\(\quad\)\(\displaystyle D_{\mathbf{v}}{f}(\mathbf{x}) = \lim_{h \rightarrow 0}{\frac{f(\mathbf{x} + h\mathbf{v}) - f(\mathbf{x})}{h}}.\)

어떤 경우에서, 그것은 벡터의 길이를 변경한 후에 방향 도함수를 계산 또는 추정하는 것이 더 쉬울 수 있을 것입니다. 종종 이것은 문제를 단위 벡터의 방향에서 방향 도함수의 계산으로 바꾸기 위해 수행됩니다. 이것이 어떻게 작동하는지 보기 위해, v = λu임을 가정하십시오. 차이 몫에 h = k/λ를 치환하십시오. 차이 몫은 다음이 됩니다:

\(\quad\)\(\displaystyle \frac{f(\mathbf{x} + (k/\lambda)(\lambda\mathbf{u})) - f(\mathbf{x})}{k/\lambda} = \lambda\cdot\frac{f(\mathbf{x} + k\mathbf{u}) - f(\mathbf{x})}{k}.\)

이것은 u에 관한 f의 방향 도함수에 대해 λ 배 차이 몫입니다. 게다가, h가 영으로 경향이 있을 때 극한을 취하함으로써, k가 영으로 경향이 있을 때 극한을 취하는 것과 같은데, 왜냐하면 h와 k가 서로의 배수이기 때문입니다. 그러므로, \(D_{\mathbf{v}}(f) = \lambda D_{\mathbf{u}}(f)\)입니다. 이 크기-재조절 속성 때문에, 방향 도함수는 오직 단위 벡터에 대해 자주 고려됩니다.

만약 f의 모든 부분 도함수가 존재하고 x에서 연속이면, 그들은 다음 공식에 의해 방향 v에서 f의 방향 도함수를 결정합니다:

\(\quad\)\(\displaystyle D_{\mathbf{v}}{f}(\boldsymbol{x}) = \sum_{j=1}^n v_j \frac{\partial f}{\partial x_j}.\)

이것은 전체 도함수(total derivative)의 정의의 결과입니다. 그것은 방향 도함수는 v에서 선형임을 따르며, \(D_{\mathbf{v}+\mathbf{w}}(f) = D_{\mathbf{v}}(f)+D_{\mathbf{w}}(f)\)임을 의미합니다.

같은 정의는 f가 \(\mathbf{R}^m\)에서 값을 갖는 함수일 때 역시 작동합니다. 위의 정의는 벡터의 각 성분에 적용됩니다. 이 경우에서, 방향 도함수는 \(\mathbf{R}^m\)에서 벡터입니다.

Total derivative, total differential and Jacobian matrix

f가 \(\mathbf{R}^n\)의 열린 부분 집합에서 \(\mathbf{R}^m\)으로 함수일 때, 선택된 방향에서 f의 방향 도함수는 해당 점에서 및 해당 방향에서 f에 대한 최상의 선형 근사입니다. 그러나 n > 1일 때, 단일 방향 도함수는 f의 행동의 완전한 그림을 제공할 수 없습니다. 전체 도함수는 한 번에 모든 방향을 고려함으로써 완벽한 그림을 제공합니다. 즉, a에서 시작하는 임의의 벡터 v에 대해, 선형 근사 공식은 유지됩니다:

\(\quad\)\(f(\mathbf{a} + \mathbf{v}) \approx f(\mathbf{a}) + f'(\mathbf{a})\mathbf{v}.\)

단일-변수 도함수와 마찬가지로, f ′(a)는 이 근사에서 오차가 가능한 한 작아지도록 선택됩니다.

만약 n과 m이 둘 다 일이면, 도함수 f ′(a)는 숫자이고 표현 f ′(a)v는 두 숫자의 곱입니다. 그러나 더 높은 차원에서, f ′(a)에 대해 숫자가 되는 것이 불가능합니다. 만약 그것이 숫자라면, f ′(a)v는 \(\mathbf{R}^n\)에서 벡터일 것이지만 다른 항은 \(\mathbf{R}^m\)에서 벡터일 것이고, 그러므로 공식은 이해되지 않습니다. 선형 근사 공식을 이해하기 위한 것에 대해, f ′(a)는 반드시 \(\mathbf{R}^n\)에서 벡터를 \(\mathbf{R}^m\)의 벡터에 보내는 함수여야 하고, f ′(a)v는 반드시 v에서 평가된 이 함수를 나타냅니다.

그것이 어떤 종류의 함수인지 결정하기 위해서, 선형 근사 공식은 다음과 같이 다시 쓰여질 수 있음을 주목하십시오:

\(\quad\)\(f(\mathbf{a} + \mathbf{v}) - f(\mathbf{a}) \approx f'(\mathbf{a})\mathbf{v}.\)

만약 우리가 다른 벡터 w를 선택하면, 이 근사 방정식은 v에 대해 w를 치환함으로써 또 다른 근사 방정식을 결정하는 것임을 주목하십시오. 그것은 v에 대해 w, a에 a + v 둘 다를 치환함으로써 세 번째 근사 방정식을 결정합니다. 이들 두 새로운 방정식을 빼는 것에 의해, 우리는 다음을 얻습니다:

\(\quad\)\(f(\mathbf{a} + \mathbf{v} + \mathbf{w}) - f(\mathbf{a} + \mathbf{v}) - f(\mathbf{a} + \mathbf{w}) + f(\mathbf{a})
\approx f'(\mathbf{a} + \mathbf{v})\mathbf{w} - f'(\mathbf{a})\mathbf{w}.\)

만약 우리는 v가 작은 것이고 도함수가 a에서 연속적으로 변한다고 가정하면, f ′(a + v)는 f ′(a)와 근사적으로 같고, 그러므로 오른쪽 변은 근사적으로 영입니다. 왼쪽 변은 v에 대해 치환된 v + w를 가진 선형 근사 공식을 사용하여 다른 방법에서 다시-쓰여질 수 있습니다. 선형 근사 공식은 다음을 암시합니다:

\(\quad\)\(\begin{align}
0
&\approx f(\mathbf{a} + \mathbf{v} + \mathbf{w}) - f(\mathbf{a} + \mathbf{v}) - f(\mathbf{a} + \mathbf{w}) + f(\mathbf{a}) \\
&= (f(\mathbf{a} + \mathbf{v} + \mathbf{w}) - f(\mathbf{a})) - (f(\mathbf{a} + \mathbf{v}) - f(\mathbf{a})) - (f(\mathbf{a} + \mathbf{w}) - f(\mathbf{a})) \\
&\approx f'(\mathbf{a})(\mathbf{v} + \mathbf{w}) - f'(\mathbf{a})\mathbf{v} - f'(\mathbf{a})\mathbf{w}.
\end{align}\)

이것은 f ′(a)가 벡터 공간 \(\mathbf{R}^n\)에서 벡터 공간 \(\mathbf{R}^m\)으로 선형 변환(linear transformation)인 것을 제안합니다. 사실, 근사에서 오차를 측정함으로써 이 정확한 유도를 만드는 것이 가능합니다. 이들 선형 근사 공식에서 오차는 상수 배 ||v||에 의해 경계되고, 여기서 상수는 v와 독립이지만 a에 연속적으로 의존한다고 가정합니다. 그런-다음, 적절한 오차 항을 더한 후, 위의 근사 방정식의 모두는 부등식으로 바꿔 말할 수 있습니다. 특히, f ′(a)는 작은 오차 항까지(up to) 선형 변환입니다. v와 w가 영으로 경향이 있을 때 극한에서, 그것은 그러므로 반드시 선형 변환이어야 합니다. 우리는 v가 영으로 다가갈 때 극한을 취함으로써 전체 도함수를 정의하므로, f ′(a)는 반드시 선형 변환이어야 합니다.

하나의 변수에서, 도함수가 최상의 선형 근사라는 사실은 그것이 차이 몫의 극한이라는 사실에 의해 표현됩니다. 어쨌든, 보통 차이 몫이 더 높은 차원에서 말이 되지 않는데, 왜냐하면 그것이 보통 벡터를 나누는 것이 가능하지 않기 때문입니다. 특히, 차이 몫의 분자와 분모는 심지어 같은 벡터 공간에서 있지 않습니다: 분자는 코도메인 \(\mathbf{R}^m\)에 놓여 있지만 분모는 도메인 \(\mathbf{R}^n\)에 놓여 있습니다. 게다가, 도함수는 선형 변환, 분자와 분모 모두로부터 대상의 다른 유형입니다. 그것은 f ′(a)가 가장 좋은 선형 근사라는 아이디어를 정확하게 만들기 위해, 이들 문제가 사라지는 일-변수 도함수에 대해 다른 공식을 적용하는 것이 필요합니다. 만약 f : R → R이면, 도함수의 보통 정의는 a에서 f의 도함수가 다음을 만족하는 고유한 숫자 f ′(a)임을 보여주기 위해 조작될 수 있을 것입니다:

\(\quad\)\(\displaystyle \lim_{h \to 0} \frac{f(a + h) - (f(a) + f'(a)h)}{h} = 0.\)

이것은 다음과 동등합니다:

\(\quad\)\(\displaystyle \lim_{h \to 0} \frac{|f(a + h) - (f(a) + f'(a)h)|}{|h|} = 0\)

왜냐하면 함수의 극한이 영으로 경향이 있는 것과 함수의 절댓값의 극한은 영으로 경향이 있는 것은 필요충분 조건이기 때문입니다. 이 마지막 공식은 노름(norm)을 갖는 절댓값을 대체함으로써 많은-변수 상황에 적용될 수 있습니다.

a에서 f의 전체 도함수(total derivative)의 정의는, 그러므로, 그것은 다음을 만족하는 고유한 선형 변환 \(f'(\mathbf{a}) : \mathbf{R}^n \to \mathbf{R}^m\)이라는 것입니다:

\(\quad\)\(\displaystyle \lim_{\mathbf{h}\to 0} \frac{\lVert f(\mathbf{a} + \mathbf{h}) - (f(\mathbf{a}) + f'(\mathbf{a})\mathbf{h})\rVert}{\lVert\mathbf{h}\rVert} = 0.\)

여기서 h는 \(\mathbf{R}^n\)에서 벡터이므로, 분모에서 노름은 \(\mathbf{R}^n\) 위의 표준 길이입니다. 어쨌든, f′(a)h는 \(\mathbf{R}^m\)에서 벡터이고, 분자에서 노름은 \(\mathbf{R}^m\) 위의 표준 길이입니다. 만약 v가 a에서 시작하는 벡터이면, f ′(a)v는 f에 의한 v의 밂(pushforward)으로 불리우고, 때때로 \(f_\mathbf{*}\mathbf{v}\)로 쓰여집니다.

만약 전체 도함수가 a에서 존재하면, f의 모든 부분 도함수와 방향 도함수가 a에서 존재하고, 모든 v에 대해, f ′(a)v는 방향 v에서 f의 방향 도함수입니다. 만약 우리가 좌표 함수를 사용하여, \(f=(f_1, f_2,\cdots, f_m)\)가 되도록, f를 쓰면, 전체 도함수는 행렬(matrix)로 부분 도함수를 사용하여 표현될 수 있습니다. 이 행렬은 a에서 f의 야코비 행렬(Jacobian matrix)이라고 불립니다:

\(\quad\)\(\displaystyle f'(\mathbf{a}) = \operatorname{Jac}_{\mathbf{a}} = \left(\frac{\partial f_i}{\partial x_j}\right)_{ij}.\)

전체 도함수 f′(a)의 존재는 모든 부분 도함수의 존재보다 엄격하게 더 강하지만, 만약 부분 도함수가 존재하고 연속이면, 전체 도함수가 존재하고, 야코비에 의해 제공되고, 연속적으로 a에 달려 있습니다.

전체 도함수의 정의는 하나의 변수에서 도함수의 정의를 포함합니다. 즉, 만약 f가 실수 변수의 실수-값 함수이면, 전체 도함수가 존재하는 것과 보통 도함수가 존재하는 것은 필요충분 조건입니다. 야코비 행렬은 1×1 행렬로 줄어들며 그의 유일한 엔트리는 도함수 f′(x)입니다. 이 1×1 행렬은 f(a + h) − (f(a) + f ′(a)h)이 근사적으로 영이라는 속성을 만족시키고, 다시 말해서 다음인 것입니다:

\(\quad\)\(f(a+h) \approx f(a) + f'(a)h.\)

변수를 변경하는 것까지(up to), 이것은 함수 \(x \mapsto f(a) + f'(a)(x-a)\)가 a에서 f에 대한 최상의 선형 근사인 명제입니다.

함수의 전체 도함수는 일-변수의 경우에서 처럼 같은 방법에서 또 다른 함수를 제공하지 않습니다. 이것은 다-변수 함수의 전체 도함수가 일-변수 함수의 도함수보다 훨씬 많은 정보를 반드시 기록해야 하기 때문입니다. 대신에, 전체 도함수는 원천의 접 묶음(tangent bundle)에서 목표의 접 묶음까지 함수를 제공합니다.

이차, 삼차, 및 더-높은 차원의 전체 도함수의 자연적 아날로그는 선형 변환이 아니고, 접 묶음의 함수가 아니고, 전체 도함수를 반복적으로 취함으로써 만들어지지 않습니다. 더 높은 차원 도함수의 아날로그는, 제트(jet)로 불리우는, 절대 선형 변환이 될 수 없는데 왜냐하면 더 높은 차원 도함수는, 오목성과 같은, 미묘한 기하학적 정보를 반영하기 때문이며, 이것은 벡터와 같은 선형 데이터의 관점에서 절대 설명될 수 없습니다. 그것은 접 묶음 위의 함수가 절대 될 수 없는데, 왜냐하면 접 묶음은 기저 공간과 방향 도함수에 대해 방을 가지기 때문입니다. 제트가 더 높은-차원 정보를 포착하기 때문에, 그들은 방향에서 고차원 변화를 나타내는 더해지는 좌표를 인수로 취합니다. 이들 더해지는 좌표에 의해 결정된 공간은 제트 묶음(jet bundle)으로 불립니다. 함수의 전체 도함수와 부분 도함수 사이의 관계는 함수의 k번째 차수 제트와 k보다 작거나 같은 차수의 부분 도함수 사이의 관계에서 유사한 것으로 예시됩니다.

전체 도함수를 반복적으로 취함으로써, 우리는 \(\mathbf{R}^p\)에 특화된, 프레셰 도함수(Fréchet derivative)의 상위 버전을 얻습니다. k번째 차수 도함수는 다음 맵핑으로 해석될 수 있을 것입니다:

\(\quad\)\(D^k f: \mathbb{R}^n \to L^k(\mathbb{R}^n \times \cdots \times \mathbb{R}^n, \mathbb{R}^m)\)

이것은 \(\mathbf{R}^n\)에서 점 x를 취하고 그것을 \(\mathbf{R}^n\)에서 \(\mathbf{R}^m\)까지 k-선형 맵의 공간의 원소로 할당합니다 – 해당 점에서 f에 대한 "최상의" (어떤 정확한 의미에서) k-선형 근사입니다. 그것을 대각선 맵(diagonal map) Δ, x → (x, x)와 함께 사전-구성함으로써, 일반화된 테일러 급수는 다음으로 시작될 수 있을 것입니다:

\(\quad\)\(\begin{align}
 f(\mathbf{x}) & \approx f(\mathbf{a}) + (D f)(\mathbf{x-a}) + (D^2 f)(\Delta(\mathbf{x-a})) + \cdots\\
 & = f(\mathbf{a}) + (D f)(\mathbf{x - a}) + (D^2 f)(\mathbf{x - a}, \mathbf{x - a})+ \cdots\\
 & = f(\mathbf{a}) + \sum_i (D f)_i (x_i-a_i) + \sum_{j, k} (D^2 f)_{j k} (x_j-a_j) (x_k-a_k) + \cdots
\end{align}\)

여기서 f(a)는 상수 함수로 식별되며, \(x_i -a_i\)는 벡터 x − a의 성분이고, \((Df)_i\)와 \((D^2f)_{jk}\)는 선형 변환으로 \(Df\)와 \(D^2f\)의 성분입니다.

Generalizations

도함수의 개념은 많은 다른 설정으로 확장될 수 있습니다. 공통 쓰레드는 한 점에서 함수의 도함수가 그 점에서 함수의 선형 근사(linear approximation)로 취급한다는 것입니다.

History

무한소 미적분학(infinitesimal calculus)으로 그의 초기 역사에서 알려진, 미적분학은 극한(limits), 함수(functions), 도함수(derivative), 적분(integral), 및 무한 급수(infinite series)에 초점을 맞춘 수학(mathematics) 분야입니다. 아이작 뉴턴(Isaac Newton)과 고트프리트 라이프니츠(Gottfried Leibniz)는 17세기 중반에서 독립적으로 미적분을 발견했습니다. 어쨌든, 각 발명가는 자신의 삶이 끝날 때까지 계속되는 격렬한 논쟁에서 자신의 일을 다른 사람이 훔쳤다고 주장했습니다.

Bibliography

Print

Online books

External links

 

 

저작자표시 비영리 변경금지

관련글

티스토리툴바