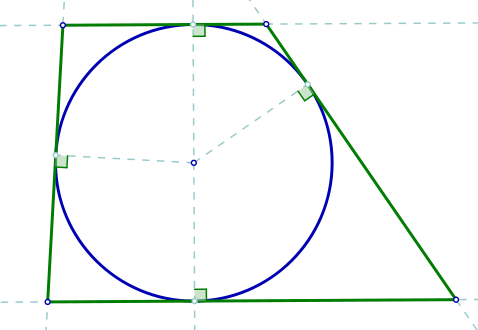
유클리드 기하학(Euclidean geometry)에서, 접하는 다각형(tangential polygon)은, 역시 둘레접된 다각형(circumscribed polygon)으로 알려져 있으며, 내접된 원(inscribed circle, 역시 내원이라고 불림)을 포함하는 볼록 다각형(convex polygon)입니다. 이것은 다각형의 각 변에 접하는(tangent) 원입니다. 접하는 다각형의 이중 다각형(dual polygon)은 각 꼭짓점(vertices)을 통과하는 둘레접된 원(circumscribed circle)을 가지는 순환 다각형(cyclic polygon)입니다.
모든 삼각형(triangles)은 접하는 것이며, 변의 개수에 관계없이 모든 정규 다각형(regular polygons)이 그렇습니다. 잘-연구된 접하는 다각형의 그룹은 마름모(rhombi)와 연(kites)을 포함하는 접하는 사변형(tangential quadrilaterals)입니다.
Characterizations
볼록 다각형이 내원을 가지는 것과 그것의 모든 내부 각도 이등분선(angle bisectors)이 공점(concurrent)인 것은 필요충분(iff) 조건입니다. 이 공통 점은 내-중심 (내원의 중심)입니다.
n개의 연속적인 변 \(a_1,...,a_n\)의 접하는 다각형이 존재하는 것과 다음 방정식의 시스템(system of equations)이
\(\quad x_1+x_2=a_1,\quad x_2+x_3=a_2,\quad \ldots,\quad x_n+x_1=a_n\)
양의 실수(reals)에서 해 \((x_1,...,x_n)\)를 가지는 것은 필요충분 조건입니다. 만약 그러한 해가 존재하면, \(x_1,...,x_n\)는 다각형의 접하는 길이입니다 (꼭짓점에서 내원이 변에 접하는(tangent) 점까지의 거리입니다).
Uniqueness and non-uniqueness
만약 변의 개수 n이 홀수이면, 위의 존재 기준을 만족시키는 변-길이 \(a_1, \dots , a_n\)의 임의의 주어진 집합에 대해, 오직 하나의 접선 다각형이 있습니다. 그러나 만약 n이 짝수이면, 그것들의 무한대가 있습니다. 예를 들어, 모든 변이 같은 사변형의 경우에서, 우리는 예각 값의 임의의 값을 갖는 마름모(rhombus)를 가질 수 있고, 모든 마름모는 내원에 접합니다.
Inradius
만약 접하는 다각형의 n 변이 \(a_1,...,a_n\)이면, 내-반지름 (내원의 반지름(radius))은 다음과 같습니다:
\(\quad\displaystyle r=\frac{K}{s}=\frac{2K}{\sum_{i=1}^n a_i}\)
여기서 K는 다각형의 넓이(area)이고 s는 반-둘레(semiperimeter)입니다. (모든 삼각형(triangles)은 접하는 것이기 때문에, 이 공식은 모든 삼각형에 적용됩니다.)
Other properties
- 홀수 개의 변을 갖는 접하는 다각형에 대해, 모든 변이 같은 것과 모든 각도가 같은 것은 필요충분 조건입니다 (따라서 그 다각형은 정규입니다). 짝수 개의 변을 갖는 접하는 다각형은 모든 같은 변을 가지는 것과 교대 각도가 같은 것은 필요충분 조건입니다 (즉, 각도 A, C, E, ...가 같고 각도 B, D, F, ...가 같습니다).
- 짝수 개의 변을 갖는 접하는 다각형에서, 홀수 번째 변의 길이의 합은 짝수 번째 변의 길이의 합과 같습니다.
- 접하는 다각형은 동일한 순서로 같은 둘레와 같은 내부 각도를 갖는 임의의 다른 다각형보다 더 큰 넓이를 가집니다.
- 임의의 접하는 다각형의 도형-중심(centroid), 경계 점의 도형-중심, 및 내접된 원의 중심은 공선형(collinear)이며, 다른 것들 사이의 다각형의 도형-중심과 경계의 도형-중심에서 보다 내-중심에서 두 배 멀리 떨어져 있습니다.
Tangential triangle
모든 삼각형은 일부 원에 접하지만, 원과 접하는 삼각형의 접선이 참조 삼각형의 꼭짓점이기도 하면 삼각형은 참조 삼각형의 접하는 삼각형(tangential triangle)이라고 불립니다.
Tangential quadrilateral
Tangential hexagon
- 접하는 육각형(hexagon) ABCDEF에서, 주요 대각선(diagonals) AD, BE, 및 CF는 브리앙숑의 정리(Brianchon's theorem)에 따라 공점(concurrent)입니다.


