
유클리드 기하학(Euclidean geometry)에서, 접하는 사변형(tangential quadrilateral, 때때로 단지 tangent quadrilateral) 또는 둘레접된 사변형(circumscribed quadrilateral)은 그것의 변 모두가 사변형 내의 단일 원(circle)에 접(tangent)할 수 있는 볼록(convex) 사변형(quadrilateral)입니다. 이 원은 사변형의 내원(incircle) 또는 그것의 내접된 원이라고 불리고, 그것의 중심은 내중심이고 그것의 반지름을 내반지름이라고 불립니다. 이들 사변형은 그것들 원을 둘러싸는 또는 둘레접하게 그려질 수 있으므로, 그것들은 역시 둘레접-가능 사변형(circumscribable quadrilaterals), 둘레접하는 사변형(circumscribing quadrilaterals), 및 둘레새김-가능 사변형(circumscriptible quadrilaterals)이라고 불려 왔니다. 접하는 사변형은 접하는 다각형(tangential polygon)의 특수한 경우입니다.
이 사변형의 클래스에 대해 다른 덜 자주 사용되는 이름은 inscriptable quadrilateral, inscriptible quadrilateral, inscribable quadrilateral, circumcyclic quadrilateral, 및 co-cyclic quadrilateral입니다. 순환 사변형(cyclic quadrilateral) 또는 내접된 사변형이라고 불리는 둘레원을 가지는 사변형과 혼동의 위험으로 인해, 마지막 다섯 가지 이름의 어떤 것을 사용하지 않는 것이 좋습니다.
모든 삼각형(triangle)은 내원을 가질 수 있지만, 모든 사변형이 내원을 가지는 것은 아닙니다. 접해질 수 없는 사변형의 예제는 비-정사각형 직사각형(rectangle)입니다. 아래의 단면 특성(characterizations)은 사변형이 내원을 가질 수 있기 위해 만족시켜야 하는 필요와 충분 조건(iff)을 말합니다.
Special cases
접하는 사변형의 예제는 마름모(rhombi)를 포함하는 연(kites)이며, 이것은 차례로 정사각형(square)을 포함합니다. 연은 역시 직교대각선(orthodiagonal)인 역시 접하는 사변형입니다. 직각 연(right kite)은 둘레원(circumcircle)을 갖는 연입니다. 만약 사변형이 접하는 및 순환(cyclic) 둘 다이면, 그것은 이-중심 사변형(bicentric quadrilateral)이라고 불리고, 만약 그것이 접하는 및 사다리꼴(trapezoid) 둘 다이면, 그것은 접하는 사다리꼴(tangential trapezoid)이라고 불립니다.
Characterizations
접하는 사변형에서, 넷의 각도 이등분선(angle bisector)은 내원의 중심에서 만납니다. 반대로, 넷의 각도 이등분선이 한 점에서 만나는 볼록 사변형은 접하는 것이어야 하고 공통 점은 내중심입니다.
피토 정리(Pitot theorem)에 따르면, 접하는 사변형에서 반대편 변의 두 쌍은 합해져서 같은 전체 길이를 가지며, 사변형의 반둘레(semiperimeter) s와 같습니다:
\(\quad\displaystyle a + c = b + d = \frac{a + b + c + d}{2} = s.\)
반대로, a + c = b + d인 볼록 사변형은 접하는 것이어야 합니다.
만약 볼록 사변형 ABCD (사다리꼴(trapezoid)이 아님)에서 반대쪽 변이 E와 F에서 교차하면, 그것이 접하는 것과 다음 중 하나인 것은 필요충분(iff) 조건입니다:
\(\quad \displaystyle BE+BF=DE+DF\)
또는
\(\quad \displaystyle AE-EC=AF-FC.\)
이들 중 두 번째는 어크하트의 정리(Urquhart's theorem)에서 상등 중 하나와 거의 같습니다. 유일한 차이점은 양쪽 변에서 부호입니다; 어크하트의 정리에서, 차이 대신 합이 있습니다.
또 다른 필요충분 조건은 볼록 사변형 ABCD가 접하는 것과 두 삼각형 ABC와 ADC에서 내원이 서로 접하는(tangent) 것은 필요충분 조건입니다.
대각선 BD와 사변형 ABCD의 네 변에 의해 형성된 각도에 관한 특성화는 이오시페스쿠(Iosifescu)에 기인입니다. 그는 1954년에 볼록 사변형이 원을 가지는 것과 다음인 것은 필요충분 조건임을 입증했습니다:
\(\quad\displaystyle \tan{\frac{\angle ABD}{2}}\cdot\tan{\frac{\angle BDC}{2}}=\tan{\frac{\angle ADB}{2}}\cdot\tan{\frac{\angle DBC}{2}}.\)
게다가, 연속적인 변 a, b, c, d를 갖는 볼록 사변형이 접하는 것과 다음인 것은 필요충분 조건입니다:
\(\quad R_aR_c=R_bR_d\)
여기서 \(R_a, R_b, R_c, R_d\)는 각각 변 a, b, c, d와 각 변에 대해 인접한 두 변의 연장선에 외부적으로 접하는 원에서 반지름입니다.
여러 더 많은 특성이 대각선에 의해 형성된 넷의 부분삼각형에서 알려져 있습니다.
Special line segments

접하는 사변형의 8개의 접선 길이 (오른쪽 그림에서 e, f, g, h)는 꼭짓점(vertex)에서 내원이 변에 접하는 점까지의 선분입니다. 각 꼭짓점에서, 둘의 합동(congruent) 접선 길이가 있습니다.
접하는 사변형의 두 접선 현(tangency chords) (그림에서 k와 l)은 내원이 이들 변에 접하는 반대편 변 위의 점을 연결하는 선분입니다. 이것들은 역시 접촉 사변형(contact quadrilateral)의 대각선(diagonal)입니다.
Area
Non-trigonometric formulas
접하는 사변형의 넓이(area) K는 다음에 의해 주어집니다:
\(\quad \displaystyle K = r \cdot s,\)
여기서 s는 반둘레(semiperimeter)이고 r은 내반지름(inradius)입니다. 또 다른 공식은 다음입니다:
\(\quad \displaystyle K = \tfrac{1}{2}\sqrt{p^2q^2-(ac-bd)^2}\)
이것은 대각선 p, q와 접하는 사변형의 변 a, b, c, d의 관점에서 제공됩니다.
그 넓이는 역시 단지 넷의 접선 길이(tangent lengths)의 관점에서 표현될 수 있습니다. 만약 이것들이 e, f, g, h이면, 접하는 사변형은 다음 넓이를 가집니다:
\(\quad \displaystyle K=\sqrt{(e+f+g+h)(efg+fgh+ghe+hef)}.\)
나아가서, 접하는 사변형의 넓이는 변 a, b, c, d와 연속적인 접선 길이 e, f, g, h의 관점에서 다음으로 표현될 수 있습니다:
\(\quad K=\sqrt{abcd-(eg-fh)^2}.\)
eg = fh인 것과 접하는 사변형이 역시 순환적이고 따라서 이-중심인 것은 필요충분 조건이므로, 이것은 최대 넓이 \(\sqrt{abcd}\)가 발생하는 것과 접하는 사변형이 이-중심인 것은 필요충분 조건임을 보여줍니다.
Trigonometric formulas
변 a, b, c, d와 두 반대편 각도의 관점에서 넓이에 대해 삼각법(trigonometric) 공식은 다음입니다:
\(\quad \displaystyle K = \sqrt{abcd} \sin \frac{A+C}{2} = \sqrt{abcd} \sin \frac{B+D}{2}.\)
주어진 변 길이에 대해, 그 넓이는 사변형이 역시 순환적이고 따라서 이중심 사변형(bicentric quadrilateral)일 때 최대(maximum)입니다. 그런-다음 \(K = \sqrt{abcd}\)인데 왜냐하면 반대편 각도는 보충 각도(supplementary angles)입니다. 이것은 미적분(calculus)을 사용하여 또 다른 방법에서 입증될 수 있습니다.
둘의 반대편 각도를 포함하는 접하는 사변형 ABCD의 넓이에 대해 또 다른 공식은 다음입니다:
\(\quad\displaystyle K=\left(IA\cdot IC+IB\cdot ID\right)\sin\frac{A+C}{2}\)
여기서 I는 내중심입니다.
사실, 그 넓이는 단지 둘의 인접한 변과 둘의 반대편 각도의 관점에서 다음으로 표현될 수 있습니다:
\(\quad\displaystyle K=ab\sin{\frac{B}{2}}\csc{\frac{D}{2}}\sin \frac{B+D}{2}.\)
여전히 또 다른 넓이 공식은 다음입니다:
\(\quad\displaystyle K=\tfrac{1}{2}|(ac-bd)\tan{\theta}|,\)
여기서 θ는 대각선 사이의 각도 중 하나입니다. 이 공식은 접하는 사변형이 연일 때 사용될 수 없는데, 왜냐하면 그때에 θ는 90°이고 탄젠트 함수는 정의되지 않기 때문입니다.
Inequalities
위에 간접적으로 언급된 것처럼, 변 a, b, c, d를 갖는 접하는 사변형의 넓이는 다음을 만족시킵니다:
\(\quad K\le\sqrt{abcd}\)
여기서 상등인 것과 그것이 이-중심 사변형(bicentric quadrilateral)인 것은 필요충분 조건입니다.
T. A. Ivanova (in 1976)에 따르면, 접하는 사변형의 반둘레 s는 다음을 만족시킵니다:
\(\quad s\ge 4r\)
여기서 r은 내반지름입니다. 상등이 있는 것과 그 사변형이 정사각형(square)인 것은 필요충분 조건입니다. 이것은 넓이 K = rs에 대해, 다음 부딩식(inequality)이 있음을 의미합니다:
\(\quad K\ge 4r^2\)
여기서 상등인 것과 접하는 사변형이 정사각형인 것은 필요충분 조건입니다.
Partition properties

내원의 중심과 사변형에 접하는 점 사이의 넷의 선분은 사변형을 넷의 직각 연(right kite)으로 나눕니다.
만약 직선이 접하는 사변형을 같은 넓이(area)와 같은 둘레(perimeter)를 갖는 둘의 다각형(polygon)으로 자르면, 그 직선은 내중심(incenter)을 통과합니다.
Inradius
연속적인 변 a, b, c, d를 갖는 접하는 사변형의 내반지름은 다음에 의해 주어집니다:
\(\quad\displaystyle r=\frac{K}{s}=\frac{K}{a+c}=\frac{K}{b+d}\)
여기서 K는 사변형의 넓이이고 s는 그것의 반둘레입니다. 주어진 변을 갖는 접하는 사변형에 대해, 내반지름은 그 사변형이 역시 순환(cyclic) (및 따라서 이-중심 사변형(bicentric quadrilateral)일 때 최대(maximum)입니다.
접선 길이(tangent lengths)의 관점에서, 내원은 다음 반지름을 가집니다:
\(\quad \displaystyle r=\sqrt{\frac{efg+fgh+ghe+hef}{e+f+g+h}}.\)
그 내반지름은 역시 내중심 I에서 접하는 사변형 ABCD의 꼭짓점까지의 거리의 관점에서 표현될 수 있습니다. 만약 u = AI, v = BI, x = CI, 및 y = DI이면, 다음입니다:
\(\quad\displaystyle r=2\sqrt{\frac{(\sigma-uvx)(\sigma-vxy)(\sigma-xyu)(\sigma-yuv)}{uvxy(uv+xy)(ux+vy)(uy+vx)}}\)
여기서 \(\sigma=\tfrac{1}{2}(uvx+vxy+xyu+yuv)\).
만약 삼각형 ABC, BCD, CDA, DAB에서 내원이 각각 반지름 \(r_1, r_2, r_3, r_4\)을 가지면, 접하는 사변형 ABCD의 내반지름은 다음에 의해 제공됩니다:
\(\quad\displaystyle r=\frac{G+\sqrt{G^2-4r_1r_2r_3r_4(r_1r_3+r_2r_4)}}{2(r_1r_3+r_2r_4)}\)
여기서 \(G=r_1r_2r_3+r_2r_3r_4+r_3r_4r_1+r_4r_1r_2\).
Angle formulas
만약 e, f, g, 및 h가 각각 꼭짓점 A, B, C, 및 D에서 내원이 접하는 사변형 ABCD의 변에 접하는 점까지의 접선 길이(tangent lengths)이면, 사변형의 각도는 다음에서 계산될 수 있습니다:
\(\quad\displaystyle \sin{\frac{A}{2}}=\sqrt{\frac{efg + fgh + ghe + hef}{(e + f)(e + g)(e + h)}},\)
\(\quad\displaystyle \sin{\frac{B}{2}}=\sqrt{\frac{efg + fgh + ghe + hef}{(f + e)(f + g)(f + h)}},\)
\(\quad\displaystyle \sin{\frac{C}{2}}=\sqrt{\frac{efg + fgh + ghe + hef}{(g + e)(g + f)(g + h)}},\)
\(\quad\displaystyle \sin{\frac{D}{2}}=\sqrt{\frac{efg + fgh + ghe + hef}{(h + e)(h + f)(h + g)}}.\)
접선 현(tangency chords) k와 l 사이의 각도는 다음에 의해 제공됩니다:
\(\quad\displaystyle \sin{\varphi}=\sqrt{\frac{(e + f + g + h)(efg + fgh + ghe + hef)}{(e + f)(f + g)(g + h)(h + e)}}.\)
Diagonals
만약 e, f, g, 및 h가 각각 A, B, C, 및 D에서 내원이 접하는 사변형 ABCD의 변에 접하는 점까지의 접선 길이(tangent lengths)이면, 대각선의 길이 p = AC와 q = BD는 다음입니다:
\(\quad \displaystyle p=\sqrt{\frac{e+g}{f+h}\Big((e+g)(f+h)+4fh\Big)},\)
\(\quad \displaystyle q=\sqrt{\frac{f+h}{e+g}\Big((e+g)(f+h)+4eg\Big)}.\)
Tangency chords
만약 e, f, g, 및 h가 접선 사변형의 접선 길이(tangent lengths)이면, 접선 현(tangency chords)의 길이는 다음입니다:
\(\quad \displaystyle k=\frac{2(efg+fgh+ghe+hef)}{\sqrt{(e+f)(g+h)(e+g)(f+h)}},\)
\(\quad \displaystyle l=\frac{2(efg+fgh+ghe+hef)}{\sqrt{(e+h)(f+g)(e+g)(f+h)}}\)
여기서 길이 k의 접선 현은 길이 a = e + f와 c = g + h의 변을 연결하고, 길이 l의 접선 현은 길이 b = f + g와 d = h + e의 변을 연결합니다. 접선 현의 제곱 비율은 다음을 만족시킵니다:
\(\quad\displaystyle \frac{k^2}{l^2} = \frac{bd}{ac}.\)
두 접선 현은
- 수직(perpendicular)인 것과 접하는 사변형이 역시 둘레원(circumcircle)을 가지는 것은 필요충분 조건입니다 (그것은 이-중심(bicentric)입니다).
- 같은 길이를 가지는 것과 접하는 사변형이 연(kite)인 것은 필요충분 조건입니다.
접하는 사변형 ABCD에서 변 AB와 CD 사이의 접선 현이 변 BC와 DA 사이의 접선 현보다 긴 것과 변 AB와 CD 사이의 쌍-중앙선(bimedian)이 변 BC와 DA 사이의 쌍중앙선보다 짧은 것은 필요충분 조건입니다.
만약 접하는 사변형 ABCD가 AB 위에 접점 W와 CD 위에 접점 Y를 가지고 접선 현 WY가 M에서 대각선 BD를 교차하면, 접선 길이 \(\tfrac{BW}{DY}\)의 비율은 대각선 BD의 선분의 비율 \(\tfrac{BM}{DM}\)과 같습니다.
Collinear points
만약 \(M_1\)과 \(M_2\)가 내중심 I를 갖는 접하는 사변형 ABCD에서 각각 대각선 AC와 BD의 중간점(midpoint)이고, 반대편 변의 쌍이 J와 K에서 만나고 M3가 JK의 중간점이면, 점 \(M_3, M_1, I\), 및 \(M_2\)는 공선형(collinear)입니다. 그것들을 포함하는 직선은 사변형의 뉴턴 직선(Newton line)입니다.
만약 접하는 사변형에서 반대편 변의 연장선이 J와 K에서 교차하고, 그것의 접촉 사변형에서 반대편 변의 연장선이 L과 M에서 교차하면, 네 점 J, L, K, 및 M은 공선형입니다.
만약 그 내원이 각각 \(T_1, T_2, T_3, T_4\)에서 변 AB, BC, CD, DA에 접하고, \(N_1, N_2, N_3, N_4\)가 대응하는 변에 관한 이들 점의 동위 켤레(isotomic conjugate)이면 (즉, \(AT_1 = BN_1\), 이런 식이면), 접하는 사변형의 나겔 점은 직선 \(N_1 N_3\)와 \(N_2 N_4\)의 교차점으로 정의됩니다. 이들 직선의 둘 다는 사변형의 둘레(perimeter)를 둘의 같은 부분으로 나눕니다. 보다 중요하게, 나겔 점 N, "넓이 도형중심" G, 및 내중심 I는 이 순서에서 공선형이고, NG = 2GI입니다. 이 직선은 접하는 사변형의 나겔 직선이라고 불립니다.
내심 I와 대각선이 P에서 교차하는 접하는 사변형 ABCD에서, \(H_X, H_Y, H_Z, H_W\)를 삼각형 AIB, BIC, CID, DIA의 직교중심(orthocenter)으로 놓습니다. 그런-다음 점 \(P, H_X, H_Y, H_Z, H_W\)는 공선형입니다.
Concurrent and perpendicular lines
둘의 대각선과 둘의 접선 현은 공점(concurrent)입니다. 이것을 보는 한 가지 방법은 그것의 모든 변이 단일 원뿔 단면(conic section)에 접하는 육각형이 한 점에서 만나는 셋의 대각선을 가진다고 말하는 브리앙숑의 정리(Brianchon's theorem)의 극한하는 경우입니다. 접하는 사변형에서, 우리는 둘의 반대편 접점에 둘의 새로운 꼭짓점을 배치함으로써 둘의 180° 각도를 갖는 육각형을 형성할 수 있습니다; 이 육각형의 모든 여섯 변은 내접된 원에 접하는 직선 위에 놓이므로, 그것의 대각선이 한 점에서 만납니다. 그러나 이들 대각선의 둘은 접하는 사변형의 대각선과 같고, 육각형의 세 번째 대각선은 둘의 반대편 접점을 통과하는 직선입니다. 다른 둘의 접점에 대해 이러한 같은 논증을 반복하면 그 결과의 증명을 완성합니다.
만약 접하는 사변형에서 반대편 변의 연장선이 J와 K에서 교차하고, 그 대각선이 P에서 교차하면, JK는 I가 내중심인 IP의 연장선과 수직입니다.
Incenter
접하는 사변형의 내중심은 그것의 뉴턴 직선(Newton line) 위에 놓입니다 (뉴턴 직선은 대각선의 중간점을 연결합니다).
접하는 사변형에서 둘의 반대편 변의 비율은 내중심 I와 다음에 따르는 꼭짓점 사이의 거리의 관점에서 표현될 수 있습니다:
\(\quad\displaystyle \frac{AB}{CD}=\frac{IA\cdot IB}{IC\cdot ID},\quad\quad \frac{BC}{DA}=\frac{IB\cdot IC}{ID\cdot IA}.\)
내중심 I를 갖는 접하는 사변형 ABCD에서 둘의 인접한 변의 곱은 다음을 만족시킵니다:
\(\quad\displaystyle AB\cdot BC=IB^2+\frac{IA\cdot IB\cdot IC}{ID}.\)
만약 I가 접하는 사변형 ABCD의 내중심이면, 다음입니다
\(\quad IA\cdot IC+IB\cdot ID=\sqrt{AB\cdot BC\cdot CD\cdot DA}.\)
접하는 사변형 ABCD에서 내중심 I가 사변형의 "꼭짓점 도형중심"과 일치하는 것과 다음인 것은 필요충분(iff) 조건입니다:
\(\quad IA\cdot IC=IB\cdot ID.\)
만약 \(M_p\)와 \(M_q\)가 내중심 I를 갖는 접하는 사변형 ABCD에서 각각 대각선 AC와 BC의 중간점(midpoint)이면, 다음입니다:
\(\quad\displaystyle \frac{IM_p}{IM_q}=\frac{IA\cdot IC}{IB\cdot ID}=\frac{e+g}{f+h}\)
여기서 e, f, g, 및 h는 각각 A, B, C, 및 D에서 접선 길이입니다. 첫 번째 상등과 이전 속성을 결합하면, 접하는 사변형의 "꼭짓점 도형중심"이 내중심과 일치하는 것과 그 내중심이 대각선의 중간점을 연결하는 선분의 중간점인 것은 필요충분 조건입니다.
만약 네-막대 린키지(four-bar linkage)가 접하는 사변형의 형식에서 만들어지면, 그것은 사변형이 볼록인 상태로 유지된다면 린키지가 어떻게 구부러져도 접하는 것으로 남게 될 것입니다. (따라서, 예를 들어, 만약 정사각형이 마름모로 변형되면, 비록 더 작은 내원에 대한 것일지라도 그것은 접하는 것으로 남습니다). 만약 한 변이 고정된 위치를 유지하면, 사변형이 구부러질 때, 내중심은 반지름 \(\sqrt{abcd}/s\)의 원을 그리며, 여기서 a,b,c,d는 순서대로 변이고 s는 반둘레입니다.
Characterizations in the four subtriangles
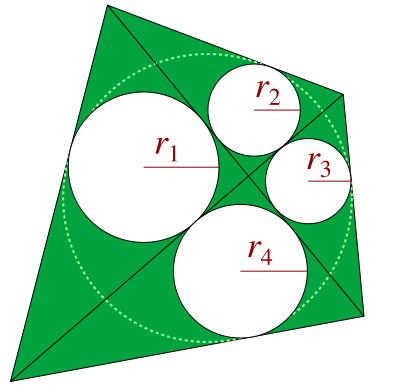
볼록 사변형 ABCD에서 대각선에 의해 형성된 겹치지 않는 삼각형 APB, BPC, CPD, DPA에서, 여기서 대각선은 P에서 교차하며, 접하는 사변형의 다음과 같은 특성이 있습니다.
\(r_1, r_2, r_3\), 및 \(r_4\)가 각각 네 삼각형 APB, BPC, CPD, 및 DPA에서 내원의 반지름을 나타낸다고 놓습니다. Chao와 Simeonov는 그 사변형이 접하는 것과 다음인 것은 필요충분(iff) 조건임을 입증했습니다:
\(\quad\displaystyle \frac{1}{r_1}+\frac{1}{r_3}=\frac{1}{r_2}+\frac{1}{r_4}.\)
이 특성화는 Vaynshtejn에 의해 5년 전에 이미 입증되었습니다. 그의 문제에 대한 해에서, 유사한 특성화가 Vasilyev와 Senderov에 의해 제공되었습니다. 만약 \(h_1, h_2, h_3\), 및 \(h_4\)가 (대각선 교차점에서 사변형의 변까지) 같은 넷의 삼각형에서 고도(altitude)를 나타내면, 그 사변형이 접하는 것과 다음인 것은 필요충분 조건입니다:
\(\quad\displaystyle \frac{1}{h_1}+\frac{1}{h_3}=\frac{1}{h_2}+\frac{1}{h_4}.\)
만약 \(R_1, R_2, R_3\), 및 \(R_4\)가 각각 삼각형 APB, BPC, CPD, and DPA의 둘레원(circumcircle)에서 반지름을 나타내면, 사변형 ABCD가 접하는 것과 다음인 것은 필요충분 조건입니다:
\(\quad\displaystyle \frac{1}{r_a}+\frac{1}{r_c}=\frac{1}{r_b}+\frac{1}{r_d}.\)
1996년에, Vaynshtejn는 접하는 사변형의 또 다른 아름다운 특성을 증명한 아마도 최초의 사람일 것이며, 그것은 나중에 여러 잡지와 웹사이트에 실렸습니다. 그것은 볼록 사변형이 그것의 둘의 대각선에 의해 넷의 겹치지 않는 삼각형으로 나뉘면, 넷의 삼각형의 내중심이 일치순환인 것과 그 사변형이 접하는 것은 필요충분 조건입니다. 사실, 그 내중심은 직교대각선 순환 사변형을 형성합니다. 관련된 결과는 내원이 외원에 대해 (사변형의 변과 그것의 대각선의 연장선에 접하는) 같은 삼각형으로 교환될 수 있다는 것입니다. 따라서 볼록 사변형은 접하는 것과 이들 넷의 외원(excircle)에서 외중심이 순환 사변형(cyclic quadrilateral)의 꼭짓점인 것은 필요충분 조건입니다.
\(\quad R_1+R_3=R_2+R_4.\)
1996년에, Vaynshtejn는 접하는 사변형의 또 다른 아름다운 특성을 증명한 아마도 최초의 사람일 것이며, 그것은 나중에 여러 잡지와 웹사이트에 실렸습니다. 그것은 볼록 사변형이 그것의 둘의 대각선에 의해 넷의 겹치지 않는 삼각형으로 나뉘면, 넷의 삼각형의 내중심이 일치순환인 것과 그 사변형이 접하는 것은 필요충분 조건입니다. 사실, 그 내중심은 직교대각선 순환 사변형을 형성합니다. 관련된 결과는 내원이 외원에 대해 (사변형의 변과 그것의 대각선의 연장선에 접하는) 같은 삼각형으로 교환될 수 있다는 것입니다. 따라서 볼록 사변형은 접하는 것과 이들 넷의 외원(excircle)에서 외중심이 순환 사변형(cyclic quadrilateral)의 꼭짓점인 것은 필요충분 조건입니다.
P에서 교차하는 대각선을 갖는 볼록 사변형 ABCD가 접하는 것과 꼭짓점 B와 B 반대편 삼각형 APB, BPC, CPD, 및 DPA에서 넷의 외중심이 순환적인 것은 필요충분 조건입니다. 만약 \(R_a, R_b, R_c\), 및 \(R_d\)가 꼭짓점 B와 D 반대편 각각 삼각형 APB, BPC, CPD, 및 DPA에서 외반지름이면, 또 다른 조건은 그 사변형이 접하는 것과 다음인 것은 필요충분 조건이라는 것입니다:
\(\quad\displaystyle \frac{1}{R_a}+\frac{1}{R_c}=\frac{1}{R_b}+\frac{1}{R_d}.\)
나아가서, P에서 교차하는 대각선을 갖는 볼록 사변형 ABCD가 접하는 것과 다음인 것은 필요충분 조건입니다:
\(\quad\displaystyle \frac{a}{\triangle(APB)}+\frac{c}{\triangle(CPD)}=\frac{b}{\triangle(BPC)}+\frac{d}{\triangle(DPA)}\)
여기서 ∆(APB)는 삼각형 APB의 넓이입니다.
대각선 교차점 P가 대각선 AC를 \(AP=p_1\)와 \(PC=p_2\)로 나누는 선분을 나타내고, 유사하게 P는 대각선 BD를 선분 \(BP=q_1\)와 \(PD=q_2\)로 나눕니다. 그런-다음 그 사변형이 접하는 것과 다음 상등 중 임의의 하나가 참인 것은 필요충분 조건입니다:
\(\quad ap_2q_2 + cp_1q_1 = bp_1q_2 + dp_2q_1\)
또는
\(\quad\displaystyle \frac{(p_1+q_1-a)(p_2+q_2-c)}{(p_1+q_1+a)(p_2+q_2+c)}=\frac{(p_2+q_1-b)(p_1+q_2-d)}{(p_2+q_1+b)(p_1+q_2+d)}\)
또는
\(\quad\displaystyle \frac{(a+p_1-q_1)(c+p_2-q_2)}{(a-p_1+q_1)(c-p_2+q_2)}=\frac{(b+p_2-q_1)(d+p_1-q_2)}{(b-p_2+q_1)(d-p_1+q_2)}.\)
Conditions for a tangential quadrilateral to be another type of quadrilateral
Rhombus
접하는 사변형이 마름모(rhombus)인 것과 그것의 반대편 각도가 같은 것은 필요충분 조건입니다.
Kite
접하는 사변형이 연(kite)인 것과 다음 조건 중 임의의 하나가 참인 것은 필요충분 조건입니다:
- 넓이는 대각선(diagonal)의 곱의 절반입니다.
- 대각선은 수직(perpendicular)입니다.
- 반대편 접점을 연결하는 둘의 선분은 같은 길이를 가집니다.
- 반대편 접선 길이(tangent lengths)의 한 쌍이 같은 길이를 가집니다.
- 쌍-중앙선(bimedians)은 같은 길이를 가집니다.
- 반대편 변의 곱은 같습니다.
- 내원의 중심은 대칭의 축인 대각선 위에 놓입니다.
Bicentric quadrilateral
만약 내원이 각각 W, X, Y, Z에서 변 AB, BC, CD, DA에 접하면, 접하는 사변형 ABCD이 역시 순환(cyclic) (및 따라서 이-중심(bicentric)인 것과 다음 조건 중 임의의 하나가 유지되는 것은 필요충분 조건입니다:
- WY는 XZ에 수직입니다.
- \(AW\cdot CY=BW\cdot DY\)
- \(\frac{AC}{BD}=\frac{AW+CY}{BX+DZ}\)
이들 셋의 첫 번째는 접촉 사변형 WXYZ가 직교대각선 사변형(orthodiagonal quadrilateral)임을 의미합니다.
접하는 사변형이 이-중심인 것과 그것의 내반지름이 변 길이의 같은 수열을 가지는 임의의 다른 접하는 사변형의 이중심보다 큰 것은 필요충분 조건입니다.
Tangential trapezoid
만약 내원이 각각 W와 Y에서 변 AB와 CD에 접하면, 접하는 사변형 ABCD는 역시 평행 변 AB와 CD를 갖는 사다리꼴(trapezoid)인 것과 다음인 것은 필요충분 조건입니다:
\(\quad AW\cdot DY=BW\cdot CY\)
그리고 AD와 BC가 사다리꼴의 평행 변인 것과 다음인 것은 필요충분 조건입니다:
\(\quad AW\cdot BW=CY\cdot DY.\)



