(번역) Solution of triangles

Original article: w:Solution of triangles

 

삼각형의 해 (Latin: solutio triangulorum)는, 삼각형(triangle)의 특성 (각도 및 변의 길이)의 일부가 알려져 있을 때, 그것을 찾기 위한 주요 삼각법의(trigonometric) 문제입니다. 삼각형은 평면(plane) 또는 구(sphere)에 위치될 수 있습니다. 삼각형 해를 요구하는 응용은 측지학(geodesy), 천문학(astronomy), 건설(construction), 및 내비게이션(navigation)을 포함합니다.

Solving plane triangles

일반적인 형식의 삼각형은 여섯 주요 특성을 가지고 있습니다 (그림 참조) : 세 개의 선분 (변 길이 a, b, c)과 세 개의 각도 (α, β, γ)가 있습니다. 고전적인 평면 삼각법 문제는 여섯 특성 중 셋을 지정하고 나머지 셋을 결정하는 것입니다. 삼각형은 다음 중 하나가 주어졌을 때 이러한 의미에서 고유하게 결정될 수 있습니다:

• 세 변 (SSS)
• 두 변과 포함된 각도 (SAS)
• 두 변과 그들 사이에 포함된 것이 아닌 각도 (SSA), 만약 그 각도에 인접한 변 길이가 나머지 변 길이보다 더 짧으면.
• 한 변과 그것에 인접한 두 각도 (ASA)
• 한 변, 그것에 반대 편 각도와 그것에 인접한 각도 (AAS).

평면에서 모든 경우에 대해, 적어도 측면 길이 중 하나가 지정되어야 합니다. 만약 오직 각도가 주어지면, 변 길이는 절대 결정되지 않는데, 왜냐하면 임의의 닮은(similar) 삼각형이 해가 아니기 때문입니다.

Trigonomic relations

문제를 해결하는 표준 방법은 기본 관계를 사용하는 것입니다.

코사인의 법칙(Law of cosines)

$a^2=b^2+c^2-2bc\cos \alpha$

$b^2=a^2+c^2-2ac\cos \beta$

$c^2=a^2+b^2-2ab\cos \gamma$

사인의 법칙(Law of sines)

${\displaystyle \frac{a}{\sin \alpha }=\frac{b}{\sin \beta }=\frac{c}{\sin \gamma }}$

각도의 합(Sum of angles)

$\alpha +\beta +\gamma ={180}^{\circ }$

탄젠트의 법칙(Law of tangents)

${\displaystyle \frac{a-b}{a+b}=\frac{\tan [\frac{1}{2}(\alpha -\beta )]}{\tan [\frac{1}{2}(\alpha +\beta )]}.}$

다른 (때로는 실질적으로 유용한) 보편적 관계: 코탄젠트의 법칙(law of cotangents)과 몰바이데의 공식(Mollweide's formula)이 있습니다.

Notes

1. 미지수 각도를 찾으려면, 코사인의 법칙(law of cosines)이 사인의 법칙(law of sines)보다 안전합니다. 그 이유는 삼각형 각도에 대한 사인(sine)의 값이 이 각도를 고유하게 결정하지 않기 때문입니다. 예를 들어, 만약 sin β = 0.5이면, 각도 β는 30° 또는 150°와 같을 수 있습니다. 코사인의 법칙을 사용하면 이 문제를 피할 수 있습니다: 0°에서 180°까지의 구간 내에서 코사인 값이 그것의 각도를 명확하게 결정합니다. 다른 한편으로, 만약 각도가 작으면 (또는 180 °에 가까우면), 아크-코사인 함수가 1 (또는 −1)에서 발산 도함수를 갖기 때문에 그것의 코사인보다 그것의 사인에서 그것을 결정하는 것이 수치적으로 보다 강건합니다.
2. 우리는 지정된 특성의 상대적 위치가 알려져 있다고 가정합니다. 그렇지 않다면, 삼각형의 거울 반사는 역시 해결책이 될 것입니다. 예를 들어, 세 변 길이는 하나의 삼각형 또는 그것의 반사를 고유하게 정의합니다.

Three sides given (SSS)

세 변 길이 a, b, c가 지정된 것으로 놓습니다. 각도 α, β를 구하기 위해, 코사인의 법칙(law of cosines)이 사용될 수 있습니다:

$\begin{array}{rl}\alpha & =\arccos \frac{b^2+c^2-a^2}{2bc}\\ \beta & =\arccos \frac{a^2+c^2-b^2}{2ac}.\end{array}$

그때의 각도는 γ = 180° − α − β입니다.

일부 출처는 사인의 법칙(law of sines)으로부터 각도 β를 찾을 것을 권장하지만 (위의 Note 1에서 언급했듯이) 예각 값과 둔각 값을 혼동할 위험이 있습니다.

알려진 변으로부터 각도를 계산하는 또 다른 방법은 코탄젠트의 법칙(law of cotangents)을 적용하는 것입니다.

Two sides and the included angle given (SAS)

여기서 변 a, b의 길이와 이들 변 사이의 각도 γ가 알려져 있습니다. 세 번째 변은 코사인의 법칙으로부터 결정될 수 있습니다:

$c=\sqrt{a^2+b^2-2ab\cos \gamma }.$

이제 우리는 두 번째 각도를 찾기 위해 코사인의 법칙을 사용합니다:

$\alpha =\arccos \frac{b^2+c^2-a^2}{2bc}.$

마지막으로, β = 180° − α − γ입니다.

Two sides and non-included angle given (SSA)

이 경우는 모든 경우에서 해결 가능한 것은 아닙니다; 하나의 해는 만약 각도에 인접한 변 길이가 나머지 변 길이보다 짧으면 고유하다는 것이 보장됩니다. 두 변 b, c와 각도 β가 알려져 있다고 가정합니다. 각도 γ에 대해 방정식은 사인의 법칙(law of sines)으로부터 암시될 수 있습니다:

${\displaystyle \sin \gamma =\frac{c}{b}\sin \beta .}$

우리는 나아가서 $D=\frac{c}{b}\sin \beta$ (방정식의 오른쪽 변)을 나타냅니다. 네 가지 가능한 경우가 있습니다:

1. 만약 D > 1이면, 그러한 삼각형이 존재하지 않는데 왜냐하면 변 b는 직선 BC에 도달하지 못하기 때문입니다. 같은 이유에 대해 만약 각도 β ≥ 90°이고 b ≤ c이면 해는 존재하지 않습니다.
2. 만약 D = 1이면, 하나의 고유한 해: γ = 90°가 존재합니다. 즉, 삼각형은 직각(right-angled)입니다.
3. 만약 D < 1이면 두 개의 대안이 가능합니다.
   1. 만약 b ≥ c이면, β ≥ γ입니다 (더 큰 변은 더 큰 각도에 해당합니다). 삼각형은 두 개의 둔각을 가질 수 없으므로, γ는 예각이고 해 γ = arcsin D는 고유합니다.
   2. 만약 b < c이면, 각도 γ는 예각: γ = arcsin D 또는 둔각: γ′ = 180° − γ일 수 있습니다. 오른쪽에 그림은 첫 번째 해로 점 C, 변 b와 각도 γ를, 두 번째 해로 점 C′, 변 b′와 각도 γ′를 보여줍니다.

한번 γ가 획득되면, 세 번째 각도는 α = 180° − β − γ입니다.

세 번째 변은 그런-다음 사인의 법칙으로부터 구할 수 있습니다:

${\displaystyle a=b\frac{\sin \alpha }{\sin \beta }}$

또는

$a=c\cos \beta \pm \sqrt{b^2-c^2{\sin }^2\beta }$

A side and two adjacent angles given (ASA)

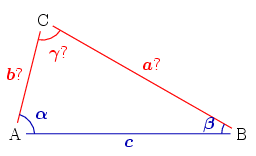
알려진 특성이 변 c와 각도 α, β입니다. 세 번째 각도는 γ = 180° − α − β입니다.

두 미지수 변은 사인의 법칙으로부터 계산될 수 있습니다:

${\displaystyle a=c\frac{\sin \alpha }{\sin \gamma };b=c\frac{\sin \beta }{\sin \gamma }.}$

또는

${\displaystyle a=c\frac{\sin \alpha }{\sin \alpha \cos \beta +\sin \beta \cos \alpha }}$

${\displaystyle b=c\frac{\sin \beta }{\sin \alpha \cos \beta +\sin \beta \cos \alpha }}$

A side, one adjacent angle and the opposite angle given (AAS)

AAS 삼각형을 푸는 절차는 ASA 삼각형에 대해 절차와 같습니다: 먼저, 삼각형의 각도 합 속성을 사용함으로써 세 번째 각도를 구합니다. 그런-다음 사인의 법칙(law of sines)을 사용하여 나머지 두 변을 구합니다.

Other given lengths

많은 경우에서, 삼각형의 중앙선(medians), 고도(altitudes), 또는 각도 이등분선(angle bisector)의 길이인 세 조각의 일부 정보가 주어지면 삼각형은 풀릴 수 있습니다. 포사멘티에와 레만은 95개의 개별적인 경우 각각에 대해 제곱근보다 높지 않은 것 (구성성(constructibility))을 사용하여 해결-가능성의 문제에 대한 결과를 나열합니다; 이들 중 63개는 구성-가능입니다.

Solving spherical triangles

일반적인 구형 삼각형은 그것의 여섯 특성 (3 변과 3 각도) 중 셋에 의해 완전하게 결정됩니다. 구형 삼각형의 변 a, b, c의 길이는 그것들의 중심 각도(central angle)이며, 선형 단위가 아닌 각도 단위에서 측정됩니다. (단위 구 위에, 각도 (라디안(radians))와 구 주위의 길이는 수치적으로 같습니다. 다른 구 위에서, 각도 (라디안)는 구 주위의 길이를 반지름으로 나눈 값과 같습니다.)

구면 기하학(spherical geometry)은 평면 유클리드 기하학(Euclidean geometry)과 다르므로, 구면 삼각형의 해는 다른 규칙을 기반으로 합니다. 예를 들어, 세 각도 α + β + γ의 합은 삼각형의 크기에 따라 다릅니다. 게다가, 닮은 삼각형(similar triangles)은 같지 않을 수 없으므로, 지정된 세 개의 각도를 갖는 삼각형을 구성하는 문제는 고유한 해를 가집니다. 문제를 해결하기 위해 사용되는 기본 관계는 평면 경우의 관계와 유사합니다: 구면 코사인 법칙(Spherical law of cosines)과 구면 사인 법칙(Spherical law of sines)을 참조하십시오.

유용할 수 있는 다른 관계 중에는 절반-변 공식(half-side formula)과 네이피어 아날로그(Napier's analogies)가 있습니다:

• ${\displaystyle \tan \frac{c}{2}\cos \frac{\alpha -\beta }{2}=\tan \frac{a+b}{2}\cos \frac{\alpha +\beta }{2}}$
• ${\displaystyle \tan \frac{c}{2}\sin \frac{\alpha -\beta }{2}=\tan \frac{a-b}{2}\sin \frac{\alpha +\beta }{2}}$
• ${\displaystyle \cot \frac{\gamma }{2}\cos \frac{a-b}{2}=\tan \frac{\alpha +\beta }{2}\cos \frac{a+b}{2}}$
• ${\displaystyle \cot \frac{\gamma }{2}\sin \frac{a-b}{2}=\tan \frac{\alpha -\beta }{2}\sin \frac{a+b}{2}.}$

Three sides given (spherical SSS)

알려진 것: 변 a, b, c (각도 단위). 삼각형의 각도는 구면 코사인 법칙(spherical law of cosines)을 사용하여 계산됩니다:

${\displaystyle \alpha =\arccos \left(\frac{\cos a-\cos b\cos c}{\sin b\sin c}\right),}$

${\displaystyle \beta =\arccos \left(\frac{\cos b-\cos c\cos a}{\sin c\sin a}\right),}$

${\displaystyle \gamma =\arccos \left(\frac{\cos c-\cos a\cos b}{\sin a\sin b}\right).}$

Two sides and the included angle given (spherical SAS)

알려진 것: 변 a, b와 그것들 사이의 각도 γ. 변 c는 구면 코사인 법칙에서 구할 수 있습니다:

$c=\arccos (\cos a\cos b+\sin a\sin b\cos \gamma ).$

각도 α, β는 위에서 처럼 계산될 수 있거나, 네이피어 아날로그에 의해 계산될 수 있습니다:

${\displaystyle \alpha =\arctan \frac{2\sin a}{\tan (\frac{\gamma }{2})\sin (b+a)+\cot (\frac{\gamma }{2})\sin (b-a)},}$

${\displaystyle \beta =\arctan \frac{2\sin b}{\tan (\frac{\gamma }{2})\sin (a+b)+\cot (\frac{\gamma }{2})\sin (a-b)}.}$

이 문제는 위도와 경도에 의해 지정된 지구 위의 두 지점 사이의 큰 원을 찾는 탐색 문제에서 발생합니다; 이 응용에서, 반올림 오류에 취약하지 않은 공식을 사용하는 것이 중요합니다. 이를 위해, 다음 공식 (벡터 대수학을 사용하여 유도될 수 있음)이 사용될 수 있습니다:

${\displaystyle \begin{array}{rl}c& =\arctan \frac{\sqrt{(\sin a\cos b-\cos a\sin b\cos \gamma {)}^2+(\sin b\sin \gamma {)}^2}}{\cos a\cos b+\sin a\sin b\cos \gamma },\\ \alpha & =\arctan \frac{\sin a\sin \gamma }{\sin b\cos a-\cos b\sin a\cos \gamma },\\ \beta & =\arctan \frac{\sin b\sin \gamma }{\sin a\cos b-\cos a\sin b\cos \gamma },\end{array}}$

여기서 이들 표현에서 분자와 분모의 부호는 아크탄젠트의 사분면을 결정하기 위해 사용되어야 합니다.

Two sides and non-included angle given (spherical SSA)

이 문제는 모든 경우에 해결할 수는 없습니다; 하나의 해는 오직 만약 각도에 인접한 변의 길이가 다른 변의 길이보다 더 짧으면 고유하다고 보장됩니다. 알려진 것: 변 b, c와 그들 사이가 아닌 각도 β. 하나의 해는 만약 다음 조건이 유지되면 존재합니다:

$b>\arcsin (\sin c\sin \beta ).$

각도 γ는 구면 사인 법칙(spherical law of sines)에서 구할 수 있습니다:

${\displaystyle \gamma =\arcsin \left(\frac{\sin c\sin \beta }{\sin b}\right).}$

평면 경우에 대한 것처럼, 만약 b < c이면 두 해: γ와 180° - γ가 있습니다.

우리는 네이피어 아날로그를 사용함으로써 다른 특징을 찾을 수 있습니다:

${\displaystyle \begin{array}{rl}a& =2\arctan [\tan (\frac{1}{2}(b-c))\frac{\sin (\frac{1}{2}(\beta +\gamma ))}{\sin (\frac{1}{2}(\beta -\gamma ))}],\\ \alpha & =2\text{arccot}[\tan (\frac{1}{2}(\beta -\gamma ))\frac{\sin (\frac{1}{2}(b+c))}{\sin (\frac{1}{2}(b-c))}].\end{array}}$

A side and two adjacent angles given (spherical ASA)

알려진 것: 변 c와 각도 α, β. 먼저 우리는 구면 코사인 법칙(spherical law of cosines)을 사용하여 각도 γ를 결정합니다:

$\gamma =\arccos (\sin \alpha \sin \beta \cos c-\cos \alpha \cos \beta ).$

우리는 (계산된 각도 γ를 사용하여) 구면 코사인 법칙에서 둘의 미지수 변을 구할 수 있습니다:

${\displaystyle a=\arccos \left(\frac{\cos \alpha +\cos \beta \cos \gamma }{\sin \beta \sin \gamma }\right),}$

${\displaystyle b=\arccos \left(\frac{\cos \beta +\cos \alpha \cos \gamma }{\sin \alpha \sin \gamma }\right),}$

또는 네이피어의 아날로그를 사용함으로써:

${\displaystyle \begin{array}{rl}a& =\arctan \left[\frac{2\sin \alpha }{\cot (\frac{c}{2})\sin (\beta +\alpha )+\tan (\frac{c}{2})\sin (\beta -\alpha )}\right],\\ b& =\arctan \left[\frac{2\sin \beta }{\cot (\frac{c}{2})\sin (\alpha +\beta )+\tan (\frac{c}{2})\sin (\alpha -\beta )}\right].\end{array}}$

A side, one adjacent angle and the opposite angle given (spherical AAS)

알려진 것: 변 a와 각도 α, β. 변 b는 구면 사인 볍칙(spherical law of sines)을 사용하여 구할 수 있습니다:

${\displaystyle b=\arcsin \left(\frac{\sin a\sin \beta }{\sin \alpha }\right).}$

만약 변 a에 대해 각도는 예각이고 α > β이면, 또 다른 해가 존재합니다:

${\displaystyle b=\pi -\arcsin \left(\frac{\sin a\sin \beta }{\sin \alpha }\right).}$

우리는 네이피어 아날로그를 사용함으로써 다른 특징을 구할 수 있습니다:

${\displaystyle \begin{array}{rl}c& =2\arctan [\tan (\frac{1}{2}(a-b))\frac{\sin (\frac{1}{2}(\alpha +\beta ))}{\sin (\frac{1}{2}(\alpha -\beta ))}],\\ \gamma & =2\text{arccot}[\tan (\frac{1}{2}(\alpha -\beta ))\frac{\sin (\frac{1}{2}(a+b))}{\sin (\frac{1}{2}(a-b))}].\end{array}}$

Three angles given (spherical AAA)

알려진 것: 각도 α, β, γ. 구면 코사인 법칙(spherical law of cosines)에서 우리는 추론합니다:

${\displaystyle a=\arccos \left(\frac{\cos \alpha +\cos \beta \cos \gamma }{\sin \beta \sin \gamma }\right),}$

${\displaystyle b=\arccos \left(\frac{\cos \beta +\cos \gamma \cos \alpha }{\sin \gamma \sin \alpha }\right),}$

${\displaystyle c=\arccos \left(\frac{\cos \gamma +\cos \alpha \cos \beta }{\sin \alpha \sin \beta }\right).}$

Solving right-angled spherical triangles

위의 알고리듬은 만약 삼각형의 각도 중 하나 (예를 들어, 각도 C)가 직각이면 훨씬 더 간단해집니다. 그러한 구면 삼각형은 그것의 둘의 원소에 의해 완전하게 정의되고, 나머지 셋은 네이피어의 오각형(Napier's Pentagon) 또는 다음 관계식을 사용하여 계산될 수 있습니다.

$\sin a=\sin c\cdot \sin A$ (구면 사인 법칙)

$\tan a=\sin b\cdot \tan A$

$\cos c=\cos a\cdot \cos b$ (구면 코사인 법칙)

$\tan b=\tan c\cdot \cos A$

$\cos A=\cos a\cdot \sin B$ (역시 구면 코사인 법칙)

$\cos c=\cot A\cdot \cot B$

Some applications

Triangulation

만약 우리가 삼각분할을 통해 해안으로부터 원격 선박까지의 거리 d를 측정하기를 원한다면, 우리는 두 지점 (기준선) 사이에 알려진 거리 l을 갖는 두 점을 해안선에 표시합니다. α, β를 기준선과 선박에 대한 방향 사이의 각도라고 놓습니다.

위의 공식으로부터 (ASA 경우, 평면 기하학을 가정하여), 우리는 거리를 삼각형 높이(triangle height)로 계산할 수 있습니다:

${\displaystyle d=\frac{\sin \alpha \sin \beta }{\sin (\alpha +\beta )}\ell =\frac{\tan \alpha \tan \beta }{\tan \alpha +\tan \beta }\ell .}$

구형 경우에 대해, 우리는 먼저 α에서 점으로부터 선박까지의 변 (즉, β의 반대편)의 길이를 ASA 공식을 통해 계산할 수 있습니다:

${\displaystyle \tan b=\frac{2\sin \beta }{\cot (l/2)\sin (\alpha +\beta )+\tan (l/2)\sin (\alpha -\beta )},}$

그리고 이것을 각도 α와 변 b와 d를 포함하는 오른쪽 부분-삼각형에 대해 AAS 공식에 대입합니다:

${\displaystyle \sin d=\sin b\sin \alpha =\frac{\tan b}{\sqrt{1+{\tan }^{2}b}}\sin \alpha .}$

(평면 공식은 실제로 l의 거듭제곱에서 구형 해의 d의 테일러 전개의 첫 번째 항입니다.)

이 방법은 연안-항해(cabotage)에서 사용됩니다. 각도 α, β는 선박으로부터 친숙한 랜드마크의 관측에 의해 정의됩니다.

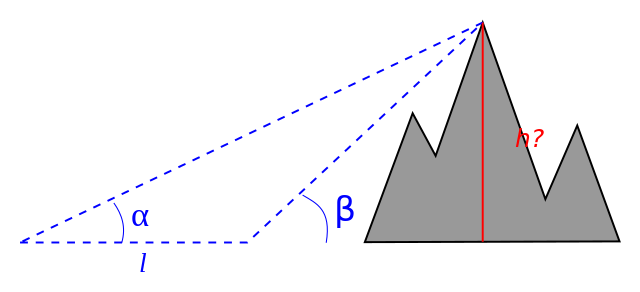
또 다른 예제로써, 만약 우리가 산 또는 높은 빌딩의 높이 h를 측정하기를 원한다면, 두 바닥 점으로부터 꼭대기까지의 각도 α, β는 지정됩니다. ℓ을 이들 점 사이의 거리로 놓습니다. 같은 ASA 경우 공식으로부터 우리는 다음을 얻습니다:

${\displaystyle h=\frac{\sin \alpha \sin \beta }{\sin (\beta -\alpha )}\ell =\frac{\tan \alpha \tan \beta }{\tan \beta -\tan \alpha }\ell .}$

The distance between two points on the globe

지구 위의 두 점 사이의 거리를 계산하기 위해,

• 점 A: 위도 ${\lambda }_A$, 경도 $L_A$, 및
• 점 B: 위도 ${\lambda }_B$, 경도 $L_B$

우리는 구면 삼각형 ABC를 고려하며, 여기서 C는 북극입니다. 일부 특징은 다음입니다:

$a={90}^{\mathrm{o}}-{\lambda }_{\mathrm{B}},$

$b={90}^{\mathrm{o}}-{\lambda }_{\mathrm{A}},$

$\gamma =L_{\mathrm{A}}-L_{\mathrm{B}}.$

만약 두 변과 포함된 각도가 주어지면, 우리는 다음 공식으로부터 얻습니다:

$\mathrm{AB}=R\arccos [\sin {\lambda }_{\mathrm{A}}\sin {\lambda }_{\mathrm{B}}+\cos {\lambda }_{\mathrm{A}}\cos {\lambda }_{\mathrm{B}}\cos (L_{\mathrm{A}}-L_{\mathrm{B}})].$

여기서 R은 지구의 반지름(Earth's radius)입니다.

External links

• Trigonometric Delights, by Eli Maor, Princeton University Press, 1998. Ebook version, in PDF format, full text presented.
• Trigonometry by Alfred Monroe Kenyon and Louis Ingold, The Macmillan Company, 1914. In images, full text presented. Google book.
• Spherical trigonometry on Math World.
• Intro to Spherical Trig. Includes discussion of The Napier circle and Napier's rules
• Spherical Trigonometry — for the use of colleges and schools by I. Todhunter, M.A., F.R.S. Historical Math Monograph posted by Cornell University Library.
• Triangulator – Triangle solver. Solve any plane triangle problem with the minimum of input data. Drawing of the solved triangle.
• TriSph – Free software to solve the spherical triangles, configurable to different practical applications and configured for gnomonic.
• Spherical Triangle Calculator – Solves spherical triangles.