본문 바로가기
영문 위키피디아 번역

(번역) Pole and polar

by 다움위키 2024. 3. 19.
Original article: w:Pole and polar

 

기하학(geometry)에서 극점(pole)과 극선(polar)은 각각 주어진 원뿔 단면(conic section)에 관한 고유한 역수 관계를 가지는 점과 직선입니다.

주어진 원에서 극 역화(Polar reciprocation)는 평면에서 각 점을 그것의 극선으로의 변환이고 평면에서 각 직선을 그것의 극으로의 변환입니다.

Properties

극점과 극선은 몇 가지 유용한 속성을 가지고 있습니다:

  • 만약 점 P가 직선 l 위에 놓이면, 직선 l의 극점 L은 점 P의 극선 p 위에 놓입니다.
  • 만약 점 P가 직선 l을 따라 이동하면, 그것의 극선 p는 직선 l의 극점 L을 중심으로 회전합니다.
  • 만약 두 개의 접선이 극점에서 원뿔 단면까지 그려질 수 있으면, 그것의 극선은 두 접점을 통과합니다.
  • 만약 한 점이 원뿔 단면 위에 놓이면, 그것의 극선은 이 점을 통과해 원뿔 단면에 접합니다.
  • 만약 점 P가 자신의 극선 위에 놓이면, P는 원뿔 단면 위에 있습니다.
  • 각 직선은, 비-퇴화 원뿔 단면에 관해, 정확하게 하나의 극점을 가집니다.

Special case of circles

원(circle) C에서 직선 L의 극점은 원의 중심에 가장 가까운 L 위의 점 P의 C에서 반전(inversion)인 점 Q입니다. 반대로, 원 C에서 점 Q의 극선(polar line 또는 polar)은 원의 중심에 가장 가까운 점 P가 C에서 Q의 반전(inversion)임을 만족하는 직선 L입니다.

극점과 극선 사이의 관계는 역수적(reciprocal)입니다. 따라서, 만약 점 A가 점 Q의 극선 q 위에 놓이면, 점 Q는 점 A의 극선 a 위에 놓여야 합니다. 두 극선 a와 q는 평행할 필요는 없습니다.

점 P가 원 C 밖에 놓이는 경우에서 점 P의 극선의 또 다른 설명이 있습니다. 이 경우에서, P를 통과하는 그 원에 접하는 두 개의 직선이 있고, P의 극선은 두 접하는 점을 연결하는 직선입니다 (여기에는 표시되지 않습니다). 이것은 극점과 극선이 평면의 투영 기하학(projective geometry)에서 개념이고 원 C의 자리에 임의의 비-특이 원뿔형(nonsingular conic)으로 일반화됨을 보여줍니다.

Polar reciprocation

하나의 극점이 있고 그것의 극선(a pole is and its polar line)이라는 개념은 투영 기하학(projective geometry)에서 발전했습니다. 예를 들어, 극선은 원뿔형에 관한 주어진 점, 극점의 투영 조화 켤레(projective harmonic conjugates)의 집합으로 볼 수 있습니다. 모든 각 점을 그것의 극선으로 교체하거나 그 반대로 교체하는 연산은 극성(polarity)이라고 불립니다.

극성(polarity)은 인볼루션(involution)이기도 한 상관관계(correlation)입니다.

어떤 점 P와 그 극선 p에 대해, p 위의 임의의 다른 점 Q는 P를 통과하는 직선 q의 극점입니다. 이것은 역수 관계를 구성하고, 투사가 보존되는 점입니다.

General conic sections

극점, 극선 및 역화의 개념은 원에서 타원(ellipse), 쌍곡선(hyperbola) 및 포물선(parabola)인 다른 원뿔 단면(conic sections)으로 일반화될 수 있습니다. 이 일반화는 원뿔 단면이 또 다른 원에서 원의 역화로 인해 발생하고, 투사(incidence) 및 교차-비율(cross-ratio)과 같은 관련된 속성이 모든 투영 변환(projective transformations) 아래에서 보존되기 때문에 가능합니다.

Calculating the polar of a point

일반적인 원뿔 단면(conic section)은 다음 평면(plane)의 데카르트 좌표(Cartesian coordinates) (x, y)에서 이-차 방정식으로 쓸 수 있습니다:

\(\quad\displaystyle 
A_{xx} x^{2} + 2 A_{xy} xy + A_{yy} y^{2} + 2 B_{x} x + 2 B_{y} y + C = 0\,
\)

여기서 \(A_{xx}, A_{xy}, A_{yy}, B_x ,B_y\), 및 C는 방정식을 정의하는 상수입니다. 그러한 원뿔 단면에 대해, 주어진 극점 (ξ, η)에 대한 극선은 다음 방정식에 의해 정의됩니다:

\(\quad\displaystyle 
D x + E y + F = 0\,
\)

여기서 D, E, 및 F는 마찬가지로 극 좌표 (ξ, η)에 따라 달라지는 상수입니다:

\(\quad\displaystyle \begin{align}
  D &= A_{xx} \xi + A_{xy} \eta + B_{x} \\
  E &= A_{xy} \xi + A_{yy} \eta + B_{y} \\
  F &= B_{x} \xi + B_{y} \eta + C\,
\end{align}\)

Calculating the pole of a line

다음 비-퇴화 원뿔 단면과 관련된 직선 \(\displaystyle  D x + E y + F = 0 \)의 극점은  

\(\quad\displaystyle 
A_{xx} x^{2} + 2 A_{xy} xy + A_{yy} y^{2} + 2 B_{x} x + 2 B_{y} y + C = 0\,
\)

두 단계에서 계산될 수 있습니다.

먼저, 다음에서 숫자 x, y, 및 z를 계산합니다:

\(\quad\displaystyle 
\begin{bmatrix}
  x \\ y \\ z
\end{bmatrix} = \begin{bmatrix}
  A_{xx} & A_{xy} & B_{x} \\
  A_{xy} & A_{yy} & B_{y} \\
  B_{x}  & B_{y}  & C
\end{bmatrix}^{-1} \cdot \begin{bmatrix}
  D \\ E \\ F
\end{bmatrix}
\)

이제, 극점은 좌표 \(\displaystyle  \left( \frac{x}{z} , \frac{y}{z} \right) \)를 갖는 점입니다.

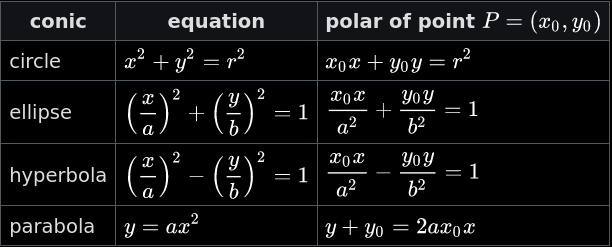
Tables for pole-polar relations

Via complete quadrangle

Complete quadrangle을 형성하는 4개의 점이 주어지면, 점을 연결하는 직선은 추가로 3개의 대각 점에서 교차합니다. 원뿔형 C 위가 아닌 점 Z가 주어지면, 점 A, B, D, 및 E에서 교차하는 Z에서 C를 통과하는 두 개의 가름선(secants)을 그립니다. 그런-다음 이들 네 점은 대각 점 중 하나에 Z를 갖는 complete quadrangle을 형성합니다. 다른 두 대각 점을 연결하는 직선은 Z의 극점이고, Z는 이 직선의 극점입니다.

Applications

극점과 극선은 조셉 디아즈 게르곤(Joseph Diaz Gergonne)에 의해 정의되었고 아폴로니우스의 문제(problem of Apollonius)를 해결하는 데 중요한 역할을 합니다.

평면 동역학에서, 극점은 회전 중심이고, 극선은 힘 작용의 직선이고 원뿔형은 질량-관성 행렬입니다. 극점-극선 관계는 평면 강체의 충격의 중심(center of percussion)을 정의하기 위해 사용됩니다. 만약 극점이 돌쩌귀 점이면, 극선은 평면 나사 이론(screw theory)에 설명된 충격 작용의 선입니다.

Bibliography

References

 

External links

관련글

티스토리툴바