(번역) Polar coordinate system

Original article: wikipedia:Polar coordinate system

수학(mathematics)에서, 극좌표 시스템(polar coordinate system)은 평면(plane) 위의 각 점(point)이 참조 점으로부터 거리(distance)와 참조 방향으로부터 각도(angle)에 의해 결정되는 이-차원(two-dimensional) 좌표 시스템(coordinate system)입니다. 참조 점 (데카르트 좌표 시스템(Cartesian coordinate system)에서 원점과 유사함)은 극점(pole)이라고 불리고, 참조 방향에서 극점으로부터 반직선(ray)은 극 축(polar axis)이라고 불립니다. 극점으로부터 거리는 방사형 좌표(radial coordinate), 방사형 거리(radial distance) 또는 간단히 반지름(radius)이라고 불리고, 각도는 각도 좌표(angular coordinate), 극 각도(polar angle), 또는 방위각(azimuth)이라고 불립니다. 극 표기법에서 각도는 일반적으로 도(degree) 또는 라디안(radian)으로 표시됩니다 (2π rad는 360°와 같습니다).

그레고와르 데 생-빈센트(Grégoire de Saint-Vincent)와 보나벤투라 카발리에리(Bonaventura Cavalieri)는 17세기 중반에 독립적으로 그 개념을 도입했지만, 실제 용어 "극 좌표"는 18세기에 그레고리오 폰타나(Gregorio Fontana)로 공인되어 왔습니다. 극 시스템의 도입에 대해 초기 동기는 원형(circular)과 궤도 운동(orbital motion)의 연구였습니다.

극 좌표는 고려 중인 현상이 나선(spiral)과 같이 평면에서 중심 점으로부터 방향과 길이에 본질적으로 묶여 있는 모든 상황에서 가장 적합합니다. 중심 점 주위로 움직이는 몸체, 또는 중심 점으로부터 유래하는 현상을 갖는 평면 물리적 시스템은 종종 극 좌표를 사용하여 모델링하는 것이 더 간단하고 직관적입니다.

극 좌표 시스템은 원통형(cylindrical)과 구형(spherical) 좌표 시스템의 두 가지 방법으로 삼-차원으로 확장됩니다.

History

각도와 반지름의 개념은 기원전 1000년경 고대 사람들에 의해 이미 사용되었습니다. 그리스의 천문학자이자 점성가, 히파르코스(Hipparchus, 기원전 190-120년)는 각 각도에 대해 현의 길이를 제공하는 현(chord) 함수 테이블을 만들었고, 별의 위치를 설정하는 데 극좌표를 사용했다는 언급이 있습니다. On Spirals에서, 아르키메데스(Archimedes)는 그 반지름이 각도에 따라 달라지는 함수, 아르키메데스 나선(Archimedean spiral)을 설명합니다. 어쨌든, 그리스 연구는 전체 좌표 시스템으로 확장되지 않았습니다.

기원후 8세기부터, 천문학자들은 지구 위의 임의의 위치에서 메카 (키블라)까지의 방향과 거리를 근사하고 계산하는 방법을 개발했습니다. 9세기부터 그들은 이들 양을 정확하게 결정하기 위해 구형 삼각법(spherical trigonometry)과 맵 투영(map projection) 방법을 사용했습니다. 그 계산은 본질적으로 메카의 적도 극 좌표(equatorial polar coordinates, 즉, 그것의 경도와 위도)를 그것의 참조 자오선이 주어진 위치와 지구의 극점을 통과하는 큰 원(great circle)과 그것의 극 축이 위치와 정반대 점(antipodal point)을 통과하는 직선인 시스템에 상대적인 극 좌표 (즉, 그것의 키블라와 거리)로 변환하는 것입니다.

형식적 좌표 시스템의 일부로 극 좌표의 도입에 대한 다양한 설명이 있습니다. 그 주제의 전체 역사는 Harvard 교수 줄리언 로웰 쿨리지(Julian Lowell Coolidge)의 Origin of Polar Coordinates에 설명되어 있습니다. 그레고와르 데 생-빈센트(Grégoire de Saint-Vincent)와 보나벤투라 카발리에리(Bonaventura Cavalieri)는 17세기 중반에 독립적으로 그 개념을 도입했습니다. 생-빈센트는 1625년에 그것들에 대해 개인적으로 썼고 1647년에 그의 연구를 출판했고, 반면에 카발리에리는 1635년에 그의 연구를 출판했고 수정된 버전은 1653년에 나타났습니다. 카발리에리는 아르키메데스 나선(Archimedean spiral) 내의 넓이와 관련된 문제를 해결하기 위해 처음으로 극 좌표를 사용했습니다. 블레즈 파스칼(Blaise Pascal)은 나중에 극 좌표를 포물선 호(parabolic arcs)의 길이를 계산하기 위해 사용했습니다.

Method of Fluxions (1671년 작성, 1736년 출판)에서, 아이작 뉴턴(Isaac Newton) 경은 그가 "Seventh Manner; For Spirals"라고 참조하는 극 좌표와, 9 개의 다른 좌표 시스템 사이의 변환을 조사했습니다. 저널 Acta Eruditorum (1691)에서 야콥 베르누이(Jacob Bernoulli)는 각각 극(pole)과 극 축(polar axis)이라고 불리는 직선 위의 점을 갖는 시스템을 사용했습니다. 좌표는 극점(pole)으로부터의 거리와 극 축(polar axis)으로부터의 각도로 지정되었습니다. 베르누이의 연구는 이들 좌표에서 표현된 곡선의 곡률 반지름(radius of curvature)을 찾는 것으로 확장되었습니다.

실제 극 좌표(polar coordinates)라는 용어는 그레고리오 폰타나(Gregorio Fontana)로 공인되어 왔고 18세기 이탈리아 작가들에 의해 사용되었습니다. 그 용어는 조지 피콕(George Peacock)의 1816년 라크루아(Lacroix)의 Differential and Integral Calculus 번역에서 영어로 나타났습니다. 알렉시 클레로(Alexis Clairaut)는 처음으로 삼차원에서 극 좌표를 생각했고, 레온하르트 오일러(Leonhard Euler)는 이를 실제로 개발했습니다.

Conventions

방사형 좌표는 종종 r 또는 ρ로 표시되고, 각도 좌표는 φ, θ, 또는 t로 표시됩니다. 각도 좌표는 ISO 표준 31-11에 의해 φ로 지정됩니다. 어쨌든, 수학 문헌에서, 각도는 종종 θ로 대신 표시됩니다.

극 좌표 표기법에서 각도는 일반적으로 도(degree) 또는 라디안(radian)으로 표시됩니다 (2π rad는 360°와 같습니다). 도는 전통적으로 항해(navigation), 측량(surveying), 및 많은 응용 분야에서 사용되고, 반면 라디안은 수학과 수학적 물리학(physics)에서 더 공동적입니다.

각도 φ는 참조 방향(reference direction)에서 0°에서 시작하여 시계 방향 (cw) 또는 반시계 방향 (ccw) 방향에서 회전할 때마다 증가하도록 정의됩니다. 예를 들어, 수학에서, 참조 방향은 보통 극점에서 오른쪽으로 수평으로 반직선으로 그려지고, 극 각도는 반시계 방향 회전에 대해 양의 각도로 증가하고, 반면에 항해 (방위각(bearing), 헤딩(heading))에서 0°-헤딩이 수직으로 위쪽으로 그려지고 시계 방향 회전에 대해 각도가 증가합니다. 극 각도는 각각 반대 방향의 회전에 대해 음수 값으로 감소합니다.

Uniqueness of polar coordinates

각도 좌표에 한 바퀴(turns, 360°)을 더하는 것은 해당 방향은 변경하지 않습니다. 유사하게, 임의의 극 좌표는 음의 방사형 구성 요소와 반대 방향 (극 각도에 180°를 더함)을 갖는 좌표와 동일합니다. 그러므로, 같은 점 (r, φ)은 무한한 숫자의 서로 다른 극 좌표 (r, φ + n × 360°)와 (−r, φ + 180° + n × 360°) = (−r, φ + (2n + 1) × 180°)로 표현될 수 있으며, 여기서 n은 임의적인 정수입니다. 게다가, 극 자체는 임의의 각도 φ에 대해 (0, φ)로 표현될 수 있습니다.

고유한 표현이 극점 이외의 임의의 점에 대해 필요한 곳에서, 보통 r을 양수 (r > 0)로 제한하고 φ를 구간 [0, 360°) 또는 구간 (−180°, 180°]으로, 라디안에서 [0, 2π) 또는 (−π, π]로 제한하는 것이 일반적입니다. 또 다른 관례는, 아크탄젠트 함수(arctan function)의 보통의 코도메인과 관련하여, 방사형 구성 요소의 임의적인 비-영 실수 값을 허용하고 극 각도를 (−90°, 90°]로 제한하는 것입니다. 모든 경우에서, 극점 (r = 0)에 대해 고유한 방위각은 선택되어야 하며, 예를 들어, φ = 0.

Converting between polar and Cartesian coordinates

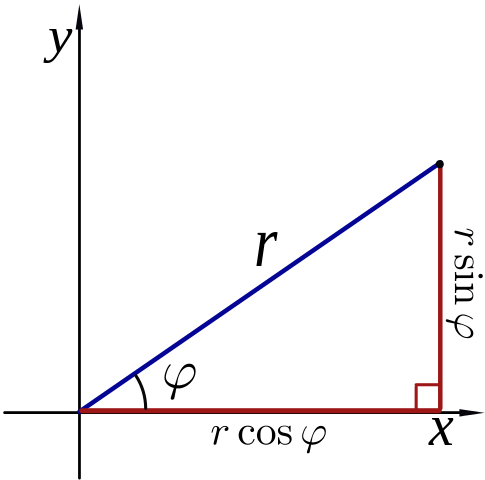
극 좌표 r과 φ는 삼각 함수(trigonometric functions) 사인과 코사인을 사용함으로써 데카르트 좌표 x와 y로 변환될 수 있습니다:

\(\quad\displaystyle \begin{align}
x &= r \cos \varphi, \\
y &= r \sin \varphi.
\end{align}\)

데카르트 좌표 x와 y는 r ≥ 0과 다음에 의해 구간 (−π, π]에서 φ를 갖는 극 좌표 r과 φ로 변환될 수 있습니다:

\(\quad\displaystyle
\begin{align}
r &= \sqrt{x^2 + y^2} = \operatorname{hypot}(x,y)\\
\varphi &= \operatorname{atan2}(y, x),
\end{align}\)

여기서 hypot는 피타고라스 합(Pythagorean sum)이고 atan2는 다음으로 정의되는 아크탄젠트(arctangent) 함수에 대한 공동적인 변형입니다:

\(\quad\displaystyle \operatorname{atan2}(y, x) = \begin{cases}
   \arctan\left(\frac{y}{x}\right)       & \mbox{if } x > 0\\
   \arctan\left(\frac{y}{x}\right) + \pi & \mbox{if } x < 0 \mbox{ and } y \ge 0\\
   \arctan\left(\frac{y}{x}\right) - \pi & \mbox{if } x < 0 \mbox{ and } y < 0\\
   \frac{\pi}{2}                         & \mbox{if } x = 0 \mbox{ and } y > 0\\
  -\frac{\pi}{2}                         & \mbox{if } x = 0 \mbox{ and } y < 0\\
   \text{undefined}                      & \mbox{if } x = 0 \mbox{ and } y = 0.
\end{cases}\)

만약 r이 위와 같이 먼저 계산되면, φ에 대한 이 공식은 아크코사인(arccosine) 함수를 사용하여 더 간단하게 나타낼 수 있습니다:

\(\quad\displaystyle \varphi = \begin{cases}
   \arccos\left(\frac{x}{r}\right) & \mbox{if } y \ge 0 \mbox{ and } r \neq 0 \\
  -\arccos\left(\frac{x}{r}\right) & \mbox{if } y < 0 \\
   \text{undefined}                & \mbox{if } r = 0.
\end{cases}\)

Complex numbers

모든 각 복소수(complex number)는 복소 평면(complex plane)에서 한 점으로 표시될 수 있고, 따라서 점의 데카르트 좌표 (직교 또는 데카르트 형식이라고 불림) 또는 점의 극 좌표(극 형식이라고 불림)를 지정함으로써 표현될 수 있습니다. 복소수 z는 다음과 같이 직교 형식으로 나타낼 수 있습니다:

\(\quad\displaystyle z = x + iy\)

여기서 i 는 허수 단위(imaginary unit)이며, 또는 대안적으로 다음과 같이 극 형식에서 쓸 수 있습니다:

\(\quad\displaystyle z = r(\cos\varphi + i\sin\varphi)\)

그리고 그 곳으로부터, 오일러 공식(Euler's formula)에 의해, 다음과 같이 쓸 수 있습니다:

\(\quad\displaystyle z = re^{i\varphi} = r \exp i \varphi. \)

여기서 e는 오일러의 숫자(Euler's number)이고, φ는, 라디안에서 표현되며, x + iy에 적용된 복소수 함수 arg의 주요 값(principal value)입니다. 복소수의 직교 형식과 극 형식 사이를 변환하기 위해, 위에 제공된 변환 공식이 사용될 수 있습니다. cis와 각도 표기법(angle notations)은 동등합니다:

\(\quad\displaystyle z = r \operatorname{\mathrm{cis}} \varphi = r \angle \varphi .\)

복소수의 곱셈(multiplication), 나눗셈(division), 지수화(exponentiation), 및 근 추출(root extraction)의 연산에 대해, 일반적으로 직교 형식이 아닌 극 형식으로 표현된 복소수로 작업하는 것이 훨씬 간단합니다. 지수화의 법칙에서:

Multiplication
- \(\displaystyle r_0 e^{i\varphi_0}\, r_1 e^{i\varphi_1} = r_0 r_1 e^{i\left(\varphi_0 + \varphi_1\right)} \)
Division:
- \(\displaystyle \frac{r_0 e^{i\varphi_0}}{r_1 e^{i\varphi_1}} = \frac{r_0}{r_1}e^{i(\varphi_0 - \varphi_1)} \)
Exponentiation (드 무아브르의 공식(de Moivre's formula))
- \(\displaystyle \left(re^{i\varphi}\right)^n = r^n e^{in\varphi} \)
Root Extraction (Principal root)
- \(\displaystyle \sqrt[n]{re^{i\varphi}} = \sqrt[n]{r} e^{i\varphi \over n} \)

Polar equation of a curve

극 좌표에서 표현되는 대수적 곡선(algebraic curve)을 정의하는 방정식은 극 방정식(polar equation)으로 알려져 있습니다. 많은 경우에서, 그러한 방정식은 r을 φ의 함수(function)로 정의함으로써 간단히 지정될 수 있습니다. 결과 곡선은 그때에 (r(φ), φ) 형식의 점으로 구성되고 극 함수 r의 그래프(graph)로 고려될 수 있습니다. 데카르트 좌표와 달리, 독립 변수 φ는 순서화된 쌍의 두 번째 엔트리임에 주목하십시오.

대칭(symmetry)의 다양한 형식이 극 함수 r의 방정식에서 추론될 수 있습니다:

만약 r(−φ) = r(φ)이면, 곡선은 수평 (0°/180°) 반직선에 대해 대칭적일 것입니다.
만약 r(π − φ) = r(φ)이면, 그것은 수직 (90°/270°) 반직선에 대해 대칭적일 것입니다.
만약 r(φ − α) = r(φ)이면, 그것은 극점에 대해 α 시계방향과 반시계방향에 의해 회전적으로 대칭적일 것입니다.

극 좌표 시스템의 원형 본성으로 인해, 많은 곡선이 다소 간단한 극 방정식으로 설명될 수 있지만, 그것들의 데카르트 형식은 훨씬 더 복잡합니다. 이들 곡선 중 가장 잘 알려진 곡선은 극선 장미(polar rose), 아르키메데스 나선(Archimedean spiral), 렘니스케이트(lemniscate), 리마숑(limaçon), 및 카디오이드(cardioid)입니다.

아래의 원, 선, 극선 장미에 대해, 곡선의 도메인과 치역에 제한이 없음을 알 수 있습니다.

Circle

\(\displaystyle (r_0, \gamma)\)에 중심을 두고 반지름 a를 갖는 원에 대한 일반적인 방정식은 다음과 같습니다:

\(\quad\displaystyle r^2 - 2 r r_0 \cos(\varphi - \gamma) + r_0^2 = a^2.\)

이것은 다음 방정식과 같은 극점에 중심을 두고 반지름 a를 갖는 원에 대해 보다 구체적인 경우에 맞게 다양한 방법으로 단순화될 수 있습니다:

\(\quad\displaystyle r(\varphi)=a \)

\(r_0=a\)이거나 원점이 원 위에 놓일 때, 그 방정식은 다음이 됩니다:

일반적인 경우에서, 그 방정식은 {{math|''r''}}에 대해 풀 수 있으며, 다음을 제공합니다:

\(\quad\displaystyle r = r_0 \cos(\varphi - \gamma) + \sqrt{a^2 - r_0^2 \sin^2(\varphi - \gamma)}\)

제곱근 앞에 빼기 기호를 갖는 해는 같은 곡선을 제공합니다.

Line

방사형 직선 (극점을 통과하는 직선)은 다음 방정식에 의해 표현됩니다:

\(\quad\displaystyle \varphi = \gamma,\)

여기서 \(\displaystyle \gamma\)는 직선의 앙각의 각도입니다; 즉, \(\displaystyle \varphi = \arctan m\), 여기서 \(\displaystyle m\)은 데카르트 좌표 시스템에서 직선의 기울기(slope)입니다. 점 \(\displaystyle (r_0, \gamma)\)에서 방사형 직선 \(\displaystyle \varphi = \gamma\)와 수직적(perpendicularly)으로 교차하는 비-방사형 직선은 다음 방정식을 가집니다:

\(\quad\displaystyle r(\varphi) = r_0 \sec(\varphi - \gamma).\)

그렇지 않으면 \(\displaystyle (r_0, \gamma)\)는 접선이 반지름 \(\displaystyle r_0\)의 허수 원과 교차하는 점임을 말합니다.

Polar rose

극선 장미(polar rose)는 꽃잎이 달린 꽃처럼 보이는 수학적 곡선으로 임의의 상수 \(\gamma_0\) (0을 포함)에 대해 다음과 같은 간단한 극 방정식으로 표현될 수 있습니다:

\(\quad\displaystyle r(\varphi) = a\cos\left(k\varphi + \gamma_0\right)\)

만약 k가 정수이면, 이들 방정식은 k가 홀수(odd)이면 k-꽃잎 장미를, k가 짝수이면 2k-꽃잎 장미를 생성할 것입니다. 만약 k가 유리수이지만 정수가 아니면, 장미-같은 모양이 형성될 수 있지만 겹치는 꽃잎을 갖습니다. 이들 방정식은 2, 6, 10, 14, 등의 꽃잎을 갖는 장미를 정의하지 못함을 주목하십시오. 변수(variable) a는 장미 꽃잎의 길이 또는 진폭을 직접 나타내고, 반면에 k는 공간 주파수와 관련됩니다. 상수 \(\gamma_0\)는 위상 각도로 고려될 수 있습니다.

Archimedean spiral

아르키메데스 나선(Archimedean spiral)은 아르키메데스에 의해 발견된 나선으로 단순한 극 방정식으로도 표현될 수 있습니다. 그것은 다음 방정식으로 표현됩니다:

\(\quad\displaystyle r(\varphi) = a + b\varphi. \)

매개변수 a를 변경하는 것은 나선을 회전시킬 것이고, 반면 b는 팔 사이의 거리를 제어하며, 이는 주어진 나선에 대해 항상 일정합니다. 아르키메데스 나선은 두 개의 팔, φ > 0에 대해 하나 φ < 0에 대해 하나를 가집니다. 두 팔은 극에서 매끄럽게 연결됩니다. 만약 a = 0이면, 90°/270° 직선을 가로질러 한쪽 팔의 거울 이미지를 취하면 다른 쪽 팔을 산출할 것입니다. 이 곡선은 원뿔 단면(conic sections) 다음으로 수학 논문에 기술된 첫 번째 곡선 중 하나이자, 극 방정식에 의해 가장 잘 정의된 곡선의 대표적인 예제로 유명합니다.

Conic sections

극 위에 한 초점과 (원뿔형의 주요 축(major axis)이 극 축을 따라 놓이도록) 0° 반직선 위의 어딘가에 나머지 한 초점을 갖는 원뿔 단면(conic section)은 다음에 의해 지정됩니다:

\(\quad\displaystyle r = { \ell\over {1 - e \cos \varphi}}\)

여기서 e는 는 이심률(eccentricity)이고 \(\displaystyle \ell\)은 반-래투스 렉텀(semi-latus rectum, 주요 축에서 곡선에 이르는 초점에서 수직 거리)입니다. 만약 e > 1이면, 이 방정식은 쌍곡선(hyperbola)을 정의합니다; 만약 e = 1이면, 그것은 포물선(parabola)을 정의합니다; 만약 e < 1이면, 그것은 타원(ellipse)을 정의합니다. 후자의 특수한 경우 e = 0은 반지름 \(\displaystyle \ell\)의 원을 초래합니다.

Intersection of two polar curves

두 개의 극 방정식 \(\displaystyle r = f(\theta)\)와 \(\displaystyle r = g(\theta)\)의 그래프는 세 가지 유형의 가능한 교차점을 가집니다:

원점에서, 만약 방정식 \(\displaystyle f(\theta) = 0\)과 \(\displaystyle g(\theta) = 0\)이 각각 적어도 하나의 해를 가집니다.
모든 점 \(\displaystyle [g(\theta_i),\theta_i]\), 여기서 \(\displaystyle \theta_i\)는 방정식 \(\displaystyle f(\theta+2k\pi)=g(\theta)\)에 대한 해이며, 여기서 \(\displaystyle k\)는 정수입니다.
모든 점 \(\displaystyle [g(\theta_i),\theta_i]\), 여기서 \(\displaystyle \theta_i\)는 방정식 \(\displaystyle f(\theta+(2k+1)\pi)=-g(\theta)\)에 대한 해이며, 여기서 \(\displaystyle k\)는 정수입니다.

Calculus

미적분(Calculus)은 극 좌표에서 표현된 방정식에 적용될 수 있습니다.

각도 좌표 φ는 이 섹션 전체에 걸쳐 라디안에서 표현되며, 이는 미적분을 수행할 때 전통적인 선택입니다.

Differential calculus

x = r cos φ와 y = r sin φ를 사용하여, 데카르트 좌표와 극 좌표에서 도함수 사이의 관계를 유도할 수 있습니다. 주어진 함수 u(x,y)에 대해, (전체 도함수(total derivatives)를 계산함으로써) 또는 다음임이 따라옵니다:

\(\quad\displaystyle \begin{align}
  r \frac{du}{dr}
    &= r \frac{\partial u}{\partial x} \cos\varphi  +
       r \frac{\partial u}{\partial y} \sin\varphi
     = x \frac{\partial u}{\partial x} + y \frac{\partial u}{\partial y}, \\[2pt]
  \frac{du}{d\varphi}
    &= - \frac{\partial u}{\partial x} r \sin\varphi +
         \frac{\partial u}{\partial y} r \cos\varphi
     = -y \frac{\partial u}{\partial x} + x \frac{\partial u}{\partial y}.
\end{align}\)

따라서, 다음과 같은 공식을 가집니다:

\(\quad\displaystyle \begin{align}
r \frac{d}{dr} &= x \frac{\partial}{\partial x} + y \frac{\partial}{\partial y} \\[2pt]
\frac{d}{d\varphi} &= -y \frac{\partial}{\partial x} + x \frac{\partial}{\partial y}.
\end{align}\)

역 좌표 변환을 사용하여, 유사한 역수 관계는 도함수 사이에 유도될 수 있습니다. 함수 u(r,φ)가 주어지면, 다음임이 따라옵니다:

\(\quad\displaystyle \begin{align}
  \frac{du}{dx}
    &= \frac{\partial u}{\partial r}\frac{\partial r}{\partial x} +
       \frac{\partial u}{\partial \varphi}\frac{\partial \varphi}{\partial x}, \\[2pt]
  \frac{du}{dy}
    &= \frac{\partial u}{\partial r}\frac{\partial r}{\partial y} +
       \frac{\partial u}{\partial \varphi}\frac{\partial \varphi}{\partial y},
\end{align}\)

또는

\(\quad\displaystyle \begin{align}
  \frac{du}{dx}
    &= \frac{\partial u}{\partial r}\frac{x}{\sqrt{x^2+y^2}} -
       \frac{\partial u}{\partial \varphi}\frac{y}{x^2+y^2} \\[2pt]
    &= \cos \varphi \frac{\partial u}{\partial r} -
       \frac{1}{r} \sin\varphi \frac{\partial u}{\partial \varphi}, \\[2pt]
  \frac{du}{dy}
    &= \frac{\partial u}{\partial r}\frac{y}{\sqrt{x^2+y^2}} +
       \frac{\partial u}{\partial \varphi}\frac{x}{x^2+y^2} \\[2pt]
    &= \sin\varphi \frac{\partial u}{\partial r} +
       \frac{1}{r} \cos\varphi \frac{\partial u}{\partial \varphi}.
\end{align}\)

따라서, 다음과 같은 공식을 가집니다:

\(\quad\displaystyle \begin{align}
  \frac{d}{dx}
    &= \cos \varphi \frac{\partial}{\partial r} -
       \frac{1}{r} \sin\varphi \frac{\partial}{\partial \varphi} \\[2pt]
  \frac{d}{dy}
    &= \sin \varphi \frac{\partial}{\partial r} +
       \frac{1}{r} \cos\varphi \frac{\partial}{\partial \varphi}.
\end{align}\)

임의의 주어진 점에서 극 곡선 r(φ)에 대한 접선의 데카르트 기울기를 찾기 위해, 그 곡선은 먼저 매개변수 방정식(parametric equations)의 시스템으로 표현됩니다:

\(\quad\displaystyle \begin{align}
x &= r(\varphi)\cos\varphi \\
y &= r(\varphi)\sin\varphi
\end{align}\)

φ에 관해 두 방정식을 미분(Differentiating)하면 다음을 산출합니다:

\(\quad\displaystyle \begin{align}
\frac{dx}{d\varphi} &= r'(\varphi)\cos\varphi - r(\varphi)\sin\varphi \\[2pt]
\frac{dy}{d\varphi} &= r'(\varphi)\sin\varphi + r(\varphi)\cos\varphi.
\end{align}\)

두 번째 방정식을 첫 번째 방정식으로 나누면 점 (r(φ), φ)에서 곡선에 대한 접선의 데카르트 기울기를 산출합니다:

\(\quad\displaystyle \frac{dy}{dx} = \frac{r'(\varphi)\sin\varphi + r(\varphi)\cos\varphi}{r'(\varphi)\cos\varphi-r(\varphi)\sin\varphi}.\)

극 좌표에서 발산, 그래디언트, 및 라플라스를 비롯한 기타 유용한 공식에 대해 곡선 좌표(curvilinear coordinates)를 참조하십시오.

Integral calculus (arc length)

극 함수에 의해 정의되는 호 길이 (선분의 길이)는 곡선 r(φ)에 걸친 적분으로 구합니다. L이 점 A에서 시작하여 점 B까지 곡선을 따라 이 길이를 나타낸다고 놓으며, 여기서 이들 점은 0 < b − a < 2π를 만족하는 φ = a와 φ = b에 해당합니다. L의 길이는 다음 적분으로 주어집니다:

\(\quad\displaystyle L = \int_a^b \sqrt{ \left[r(\varphi)\right]^2 + \left[ {\tfrac{dr(\varphi) }{ d\varphi }} \right] ^2 } d\varphi\)

Integral calculus (area)

R은 곡선 r(φ)과 반직선 φ = a와 φ = b로 둘러싸인 영역을 나타낸다고 놓으며, 여기서 0 < b − a ≤ 2π입니다. 그런-다음 R의 면적은 다음과 같습니다:

\(\quad\displaystyle \frac12\int_a^b \left[r(\varphi)\right]^2\, d\varphi.\)

이 결과는 다음과 같이 확인될 수 있습니다. 먼저, 구간 [a, b]는 n 개의 부분구간으로 나뉘며, 여기서 n은 양의 정수입니다. 따라서 Δφ, 각 부분구간의 각도 측정은 b − a (그 구간의 전체 각도 측정)를, n, 부분구간의 개수로 나눈 것과 같습니다. 각 부분구간 i = 1, 2, ..., n에 대해, \(\varphi_i\)를 부분구간의 중간점으로 놓고 극점에 중심을 두고, 반지름 \(r(\varphi_i)\), 중심 각도 Δφ, 및 호 길이 \(r(\varphi_i)\Delta \varphi\)를 갖는 부채꼴(sector)을 구성한다고 놓습니다. 구성된 각 부채꼴의 넓이는 그때에 다음과 같습니다:

\(\quad\displaystyle \left[r(\varphi_i)\right]^2 \pi \cdot \frac{\Delta \varphi}{2\pi} = \frac{1}{2}\left[r(\varphi_i)\right]^2 \Delta \varphi.\)

따라서 모든 부채꼴의 총 넓이는 다음과 같습니다:

\(\quad\displaystyle \sum_{i=1}^n \tfrac12r(\varphi_i)^2\,\Delta\varphi.\)

부분구간 n의 숫자가 증가함에 따라, 넓이의 근사가 향상됩니다. n → ∞를 취하면, 그 합은 위의 적분에 대해 리만 합(Riemann sum)이 됩니다.

넓이 적분을 계산하는 기계 장치는 평면 도형을 추적함으로써 그것의 넓이를 측정하는 플래니미터(planimeter)입니다; 이것은 2-원소 린키지(linkage)가 그린의 정리(Green's theorem)에 영향을 미치고, 이차 극 적분을 선형 적분으로 변환하도록 관절을 추가함으로써 극 좌표에서 적분을 복제합니다.

Generalization

데카르트 좌표(Cartesian coordinates)를 사용하면, 무한소 넓이 원소가 dA = dx dy로 계산될 수 있습니다. 다중 적분에 대해 대안적인 규칙에 따르면, 다른 좌표를 사용할 때, 좌표 변환 공식의 야코비(Jacobian) 행렬식이 고려되어야 합니다:

\(\quad\displaystyle J = \det \frac{\partial(x, y)}{\partial(r, \varphi)}
  = \begin{vmatrix}
      \frac{\partial x}{\partial r} & \frac{\partial x}{\partial \varphi} \\[2pt]
      \frac{\partial y}{\partial r} & \frac{\partial y}{\partial \varphi}
    \end{vmatrix}
  = \begin{vmatrix}
      \cos\varphi & -r\sin\varphi \\
      \sin\varphi &  r\cos\varphi
    \end{vmatrix}
  = r\cos^2\varphi + r\sin^2\varphi = r.
\)

따라서, 극 좌표에서 넓이 원소는 다음으로 쓸 수 있습니다:

\(\quad\displaystyle dA = dx\,dy\ = J\,dr\,d\varphi = r\,dr\,d\varphi.\)

이제, 극 좌표에서 주어진 함수는 다음과 같이 적분될 수 있습니다:

\(\quad\displaystyle \iint_R f(x, y)\, dA = \int_a^b \int_0^{r(\varphi)} f(r, \varphi)\,r\,dr\,d\varphi.\)

여기서, R은 위에서와 같은 영역, 즉, 곡선 r(φ)과 반직선 φ = a와 φ = b로 둘러싸인 영역입니다. R의 넓이에 대한 공식은 f를 1과 완전 똑같이 취함으로써 검색됩니다.

이 결과의 더 놀라운 적용은 다음 가우스 적분(Gaussian integra)을 산출합니다:

\(\quad\displaystyle \int_{-\infty}^\infty e^{-x^2} \, dx = \sqrt\pi.\)

Vector calculus

벡터 미적분(Vector calculus)은 극 좌표에도 적용될 수 있습니다. 평면 운동에 대해, \(\displaystyle \mathbf{r}\)을 시간 t에 의존하는 r과 φ를 갖는 위치 벡터 (r cos(φ), r sin(φ))라고 놓습니다.

우리는 \(\displaystyle \mathbf{r}\)의 방향에서 다음 단위 벡터를 정의합니다:

\(\quad\displaystyle \hat{\mathbf{r}} = (\cos(\varphi), \sin(\varphi))\)

그리고 반사형 방향에 수직인 운동의 평면에서 다음을 정의합니다:

\(\quad\displaystyle \hat{\boldsymbol \varphi} = (-\sin(\varphi), \cos(\varphi)) = \hat{\mathbf{k}} \times \hat{\mathbf{r}} \ ,\)

여기서 \(\displaystyle \hat{\mathbf{k}}\)는 운동의 평면에 법선인 단위 벡터입니다.

그런-다음

\(\displaystyle \begin{align}
         \mathbf{r} &= (x,\ y) = r(\cos\varphi,\ \sin\varphi) = r \hat{\mathbf{r}}\ , \\
   \dot{\mathbf{r}} &= \left(\dot{x},\ \dot{y}\right) = \dot{r}(\cos\varphi,\ \sin\varphi) + r\dot{\varphi}(-\sin\varphi,\ \cos\varphi) = \dot{r}\hat{\mathbf{r}} + r\dot{\varphi}\hat{\boldsymbol{\varphi}}\ ,\\
  \ddot{\mathbf{r}} &= \left(\ddot{x},\ \ddot{y}\right) \\
                    &= \ddot{r}(\cos\varphi,\ \sin\varphi) + 2\dot{r}\dot{\varphi}(-\sin\varphi,\ \cos\varphi) +  r\ddot{\varphi}(-\sin\varphi,\ \cos\varphi) - r\dot{\varphi}^2(\cos\varphi,\ \sin\varphi) \\
                    &= \left(\ddot{r} - r\dot{\varphi}^2\right) \hat{\mathbf{r}} + \left(r\ddot{\varphi} + 2\dot{r}\dot{\varphi}\right) \hat{\boldsymbol{\varphi}} \\
                    &= \left(\ddot{r} - r\dot{\varphi}^2\right) \hat{\mathbf{r}} + \frac{1}{r}\; \frac{d}{dt} \left(r^2\dot{\varphi}\right) \hat{\boldsymbol{\varphi}}.
\end{align}\)

이 방정식은 함수의 도함수와 단위 기저 벡터의 도함수를 취함으로써 얻을 수 있습니다.

매개변수 \(\displaystyle \theta\)를 갖는 2D에서 곡선에 대해 이전 방정식은 다음과 같이 단순화됩니다:

\(\quad\displaystyle \begin{aligned}
\vec r &= r(\theta) \hat e_r\\
\frac {d\vec r} {d\theta} &= \frac {dr} {d\theta}\hat e_r+r\hat e_\theta\\
\frac {d^2\vec r} {d\theta^2} &= (\frac {d^2 r} {d\theta^2}-r) \hat e_r +\frac {dr} {d\theta} \hat e_\theta
\end{aligned}\)

Centrifugal and Coriolis terms

항 \(\displaystyle r\dot\varphi^2\)는 때때로 구심 가속도(centripetal acceleration)라고 참조되고, 항 \(\displaystyle 2\dot r \dot\varphi\)는 코리올리 가속도(Coriolis acceleration)라고 참조됩니다. 예를 들어 Shankar를 참조하십시오.

참고: 가속도가 극 좌표에서 표현될 때 나타나는 이들 항은 미분화의 수학적 결과입니다; 그것들은 극 좌표가 사용될 때마다 나타납니다. 평면 입자 동역학에서, 이들 가속도는 회전하는 참조 프레임에서 뉴턴의 두 번째 운동 법칙(second law of motion)을 설정할 때 나타납니다. 여기서 이들 여분의 항은 종종 가상의 힘(fictitious forces)이라고 불립니다; 그것들은 단순히 좌표 프레임에서 변화의 결과이기 때문에 가상적입니다. 그것이 그것들이 존재하지 않는다는 것이 아니라, 오히려 그것들이 회전하는 프레임에만 존재한다는 의미입니다.

Co-rotating frame

평면 운동에서 입자에 대해, 이들 항에 물리적 의미를 부여하는 한 가지 접근 방식은 순간적인 공동-회전 참조 프레임(co-rotating frame of reference)의 개념을 기반으로 합니다. 공동-회전 프레임을 정의하기 위해, 먼저 원점이 입자까지의 거리 r(t)가 정의되는 것에서 선택합니다. 회전의 축은 입자의 운동의 평면에 수직이고, 이 원점을 통과하는 것으로 설정됩니다. 그런-다음, 선택된 순간 t에서, 공동-회전 프레임 Ω의 회전의 율은 이 축에 대한 입자의 회전의 율, dφ/dt와 일치하도록 합니다. 다음으로, 관성 프레임에서 가속도에서 그 항은 공동-회전 프레임에서 항과 관련됩니다. 관성 프레임에서 입자의 위치를 (r(t), φ(t))라고 놓고, 공동-회전 프레임에서 (r′(t), φ′(t))라고 놓습니다. 공동-회전 프레임은 입자와 같은 율로 회전하기 때문에, dφ′/dt = 0입니다. 공동-회전 프레임의 가상 원심력은 반사형 바깥쪽으로 \(mr\Omega^2\)입니다. 공동-회전 프레임에서 입자의 속도도 dφ'/dt = 0이기 때문에 방사형 바깥쪽입니다. 가상의 코리올리 힘은 따라서 φ만 증가하는 방향을 가리키는 −2m(dr/dt)Ω 값을 가집니다. 따라서, 뉴턴의 두 번째 법칙에서 이들 힘을 사용하여 다음을 찾습니다:

\(\quad\displaystyle \boldsymbol{F} + \boldsymbol{F}_\text{cf} + \boldsymbol{F}_\text{Cor} = m\ddot{\boldsymbol{r}} \ , \)

여기서 문자 위의 점은 시간 차이를 나타내고, F는 (가상 힘과 반대로) 순 실제 힘입니다. 성분의 측면에서, 이 벡터 방정식은 다음이 됩니다:

\(\quad\displaystyle \begin{align}
F_r + mr\Omega^2 &= m\ddot{r} \\
F_\varphi - 2m\dot{r}\Omega &= mr\ddot{\varphi} \ ,
\end{align}\)

이는 관성 프레임에 대해 방정식과 비교될 수 있습니다:

\(\quad\displaystyle \begin{align}
F_r &= m\ddot{r} - mr\dot{\varphi}^2 \\
F_\varphi &= mr\ddot{\varphi} + 2m\dot{r}\dot{\varphi} \ .
\end{align}\)

이 비교는, 시간 t에서의 공동-회전 프레임의 정의에 의해 회전의 율 Ω = dφ/dt를 가진다는 인식과 함께, 관성 프레임에서 발견되는 가속도 (입장의 질량을 곱한 값)에서 항들을 순간, 비-관성 공동-회전 프레임에서 볼 수 있는 원심력과 코리올리 힘의 음수로 해석할 수 있음을 보여줍니다.

입자의 일반 운동 (단순 원형 운동과 반대)에 대해, 입자의 참조 프레임에 있는 원심력과 코리올리 힘은 공동적으로 극 좌표의 고정된 중심이 아니라 그 운동의 순간 진동 원(osculating circle)을 참조합니다. 자세한 내용에 대해 구심력(centripetal force)을 참조하십시오.

Differential geometry

미분 기하학(differential geometry)의 현대 용어에서, 극 좌표는 미분-가능 매니폴드(differentiable manifold) \(\mathbf{R}^2 \backslash \{(0,0)\}\), 평면 빼기 원점에 대한 좌표 차트(coordinate charts)를 제공합니다. 이들 좌표에서, 유클리드 메트릭 텐서(metric tensor)는 다음에 의해 제공됩니다:

\(\quad\displaystyle ds^2 = dr^2 + r^2 d\theta^2.\)

이것은 메트릭 텐서에 대해 변수의 변경 공식을 통해, 또는 0-형식 x = r cos(θ), y = r sin(θ)의 외부 도함수(exterior derivative)를 통해 미분 형식(differential forms) dx, dy를 계산하고 그것들을 유클리드 메트릭 텐서 \(ds^2 = dx^2+dy^2\)에서 대입함으로써 볼 수 있습니다. 에 있습니다. 이 메트릭에 관한 직교-정규(orthonormal) 프레임(frame)은 다음에 의해 제공됩니다:

\(\quad\displaystyle e_r = \frac{\partial}{\partial r}, \quad e_\theta = \frac1r \frac{\partial}{\partial \theta},\)

이때, 이중 공동-프레임(dual coframe)을 가집니다:

\(\quad\displaystyle e^r = dr, \quad e^\theta = r d\theta.\)

이 프레임과 레비-치비타 연결(Levi-Civita connection)에 관한 연결 형식(connection form)은 1-형식의 반-대칭 행렬에 의해 주어집니다:

\(\quad\displaystyle {\omega^i}_j = \begin{pmatrix} 0 & -d\theta \\ d\theta & 0\end{pmatrix}\)

그리고 따라서 곡률 형식(curvature form) Ω = dω + ω∧ω은 사라집니다. 그러므로, 예상대로, 구멍-뚫린 평면은 플랫 매니폴드(flat manifold)입니다.

Extensions in 3D

극 좌표 시스템은 원통형 좌표 시스템(cylindrical coordinate system) 과 구형 좌표 시스템(spherical coordinate system)의 두 가지 좌표 시스템과 함께 삼-차원으로 확장됩니다.

Applications

극 좌표는 dl-차원이고 따라서 그것들은 점 위치가 단일 이-차원 평면에 놓이는 경우에만 사용될 수 있습니다. 그것들은 고려되는 현상이 본질적으로 중심 점으로부터의 방향과 길이와 관련된 임의의 맥락에서 가장 적절합니다. 예를 들어, 위의 예제는 데카르트 좌표 시스템에서 그 방정식이 훨씬 더 복잡할 수 있는 아르키메데스 나선과 같은 곡선을 정의하기 위해 기본 극 방정식이 어떻게 충분한지 보여줍니다. 더욱이, 중심 점 주위를 움직이는 물체 또는 중심 점에서 발생하는 현상과 관련된 많은 물리적 시스템은 극 좌표를 사용하여 모델링하는 것이 더 간단하고 직관적입니다. 극 시스템의 도입에 대해 초기 동기는 원형 운동(circular motion)과 궤도 운동(orbital motion)의 연구였습니다.

Position and navigation

극 좌표는 항법(navigation)에서 목적지 또는 이동의 방향이 고려 중인 물체로부터의 각도와 거리로 제공될 수 있을 때 자주 사용됩니다. 예를 들어, 항공기는 항법을 위해 약간 수정된 버전의 극 좌표를 사용합니다. 이 시스템에서, 일반적으로 모든 종류의 항법에 사용되는 0° 반직선은 일반적으로 헤딩 360이라고 불리고, 각도는 수학 시스템에서와 같이 반시계 방향이 아니라 시계 방향으로 계속됩니다. 헤딩 360은 자기 북쪽(magnetic north)에 해당하고, 반면에 헤딩 90, 180, 및 270은 각각 자기 동쪽, 남쪽, 및 서쪽에 해당합니다. 따라서, 동쪽으로 5 해리를 이동하는 항공기는 헤딩 90 (항공 교통 관제소에 의해 0-9-0(zero-niner-zero)으로 읽힘)에서 5 단위를 이동하게 됩니다.

Modeling

방사형 대칭(radial symmetry)을 표시하는 시스템은 극점 역할을 하는 중심 점과 함께 극 좌표 시스템에 대해 자연스러운 설정을 제공합니다. 이 사용법의 주요 예제는 방사형 대칭 우물에 적용될 때 지하수 흐름 방정식(groundwater flow equation)입니다. 반사형 힘(radial force)을 갖는 시스템도 극 좌표 시스템을 사용하기에 좋은 후보입니다. 이들 시스템은 역-제곱 법칙(inverse-square law)을 따르는 중력 필드(gravitational fields)와 라디오 안테나(radio antennas)와 같은 점 소스(point sources)를 갖는 시스템을 포함합니다.

방사형 비-대칭 시스템은 극 좌표로 모델링될 수도 있습니다. 예를 들어, 마이크의 픽업 패턴(pickup pattern)은 주어진 방향에서 들어오는 소리에 대한 비례 응답을 나타내고, 이들 패턴은 극 곡선으로 나타낼 수 있습니다. 가장 공통적인 단일방향성 마이크, 표준 카디오이드 마이크에 대한 곡선은 그것의 목표 설계 주파수에서 r = 0.5 + 0.5sin(ϕ)으로 나타낼 수 있습니다. 그 패턴은 더 낮은 주파수에서 전방향성(omnidirectionality)으로 이동합니다.

Dawoum

(번역) Polar coordinate system

History