기본 기하학(geometry)에서, 둘의 기하학적 대상은 만약 그것들이 직각(right angle) (90도 또는 π/2 라디안)으로 교차(intersect)하면 수직입니다.
만약 두 직선이 직각으로 교차하면 직선은 또 다른 직선에 수직이라고 말합니다. 명시적으로, 만약 (1) 두 직선이 만나고; (2) 교차점에서 첫 번째 직선의 한 변에 있는 직진 각도(straight angle)는 두 번째 직선에 의해 둘의 합동(congruent) 각도(angle)로 절단되면, 첫 번째 직선이 두 번째 직선에 수직입니다. 수직성은 대칭(symmetric)으로 표시될 수 있으며, 만약 첫 번째 직선이 두 번째 직선에 수직이면 두 번째 직선은 역시 첫 번째 직선에 수직임을 의미합니다. 이러한 이유로, 우리는 순서 지정 없이 두 직선을 (서로에) 수직이라고 말할 수 있습니다.
수직성은 선분(segment)과 광선(ray)으로 쉽게 확장됩니다. 예를 들어, 선분 \(\overline{AB}\)는 만약, 각각이 무한 직선을 형성하기 위해 양쪽 방향으로 확장될 때, 이들 두 결과 직선은 위의 의미에서 수직이면 선분 \(\overline{CD}\)에 수직입니다. 기호에서, \(\overline{AB} \perp \overline{CD}\)는 선분 AB가 선분 CD와 수직임을 의미합니다. 수직 기호에 대한 정보에 대해 업 택(Up tack)을 참조하십시오.
직선이 만약 그것이 교차하는 평면에서 모든 각 직선에 수직이면 직선은 평면(plane)에 수직이라고 말합니다. 이 정의는 직선 사이의 수직성의 정의에 따라 다릅니다.
공간에서 두 평면은 만약 그것들이 만나는 이면 각도(dihedral angle)가 수직이면 수직이라고 말합니다.
수직성은 직교성(orthogonality)의 보다 일반적인 수학적 개념의 한 가지 특정 사례입니다; 수직성은 고전적인 기하학적 대상의 직교성입니다. 따라서, 고급 수학에서, 단어 "수직"은 표면과 그것의 법선(normal) 사이의 수직성과 같은 훨씬 더 복잡한 기하학적 직교성 조건을 설명하기 위해 사용됩니다.
Foot of a perpendicular
단어 발(foot)은 수직과 관련하여 자주 사용됩니다. 이 사용법은 위의 꼭대기 다이어그램과 그것의 캡션에 예시되어 있습니다. 그 다이어그램은 임의의 방향이 될 수 있습니다. 그 발이 반드시 바닥에 있지는 않습니다.
보다 정확하게, A를 한 점으로 놓고 m을 한 직선이라고 놓습니다. 만약 B가 m과 m에 수직인 A를 통과하는 고유한 직선의 교차점이면, B는 A를 통과하는 이 수직선의 발이라고 불립니다.
Construction of the perpendicular
 |
 |
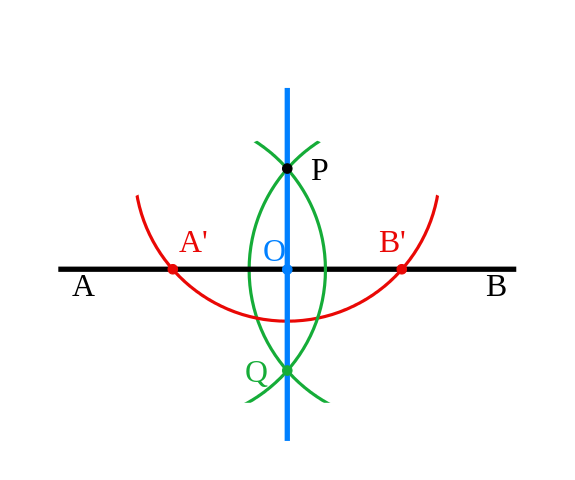
컴퍼스와 직선자 구성(compass-and-straightedge construction)을 사용하여 점 P를 통과하는 직선 AB에 수직을 만들기 위해, 다음과 같이 진행하십시오 (왼쪽 그림을 참조하십시오):
- 단계 1 (빨간색): P에서 간은-거리(equidistant)에 있는 직선 AB 위에 점 A' 및 B'을 생성하기 위해 P에 중심을 갖는 원(circle)을 구성합니다.
- 단계 2 (초록색): 같은 반지름을 가지는 A' 및 B'에 중심을 둔 원을 구성합니다. Q와 P를 이들 두 원의 교차의 점으로 놓습니다.
- 단계 3 (파란색): 원했던 수직 PQ를 구성하기 위해 Q와 P를 연결합니다.
PQ가 AB에 수직임을 입증하기 위해, QPA'과 QPB'에 대해 SSS 합동 정리를 사용하여 각도 OPA'와 OPB'가 같다는 결론을 내립니다. 그런-다음 삼각형 OPA'와 OPB'에 대해 SAS 합동 정리를 사용하여 각도 POA와 POB가 같다는 결론을 내립니다.
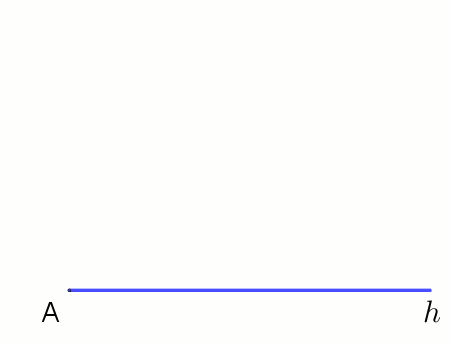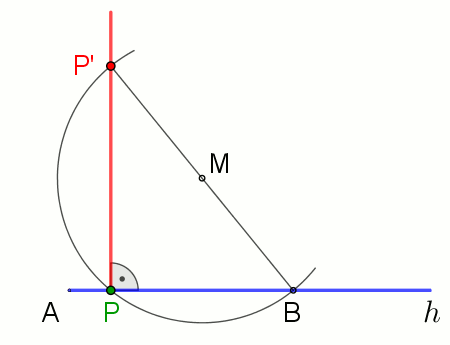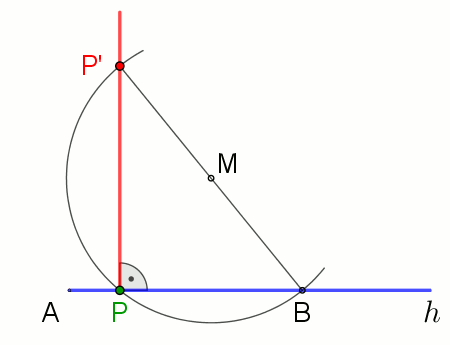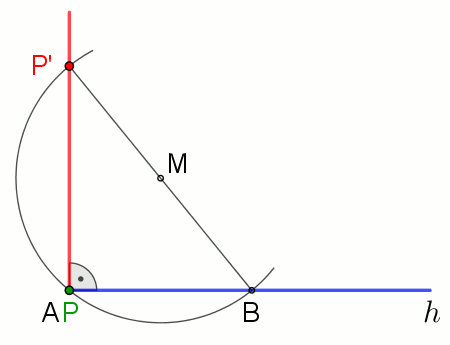
탈레스의 정리(Thales's theorem)를 사용하여 점 P에서 또는 점 P를 통과하는 직선 g에 수직을 만들기 위해, 오른쪽의 애니메이션을 참조하십시오.
피타고라스 정리(Pythagorean theorem)는 직각을 구성하는 방법의 기초로 사용될 수 있습니다. 예를 들어, 링크를 셈으로써, 셋의 체인 조각이 3:4:5 비율에서 길이를 갖도록 만들어질 수 있습니다. 이것들은 삼각형을 형성하도록 배치될 수 있으며, 이 삼각형은 그것의 가장 긴 변의 반대쪽에 직각을 가질 것입니다. 이 방법은 치수가 크고, 높은 정확도가 필요하지 않은 정원과 들판을 배치하는 데 유용합니다. 체인은 필요할 때마다 반복적으로 사용될 수 있습니다.
In relationship to parallel lines

만약 두 직선 (a와 b)가 모두 세 번째 직선 (c)에 수직이면, 세 번째 직선을 따라 형성된 모든 각도는 직각입니다. 그러므로, 유클리드 기하학(Euclidean geometry)에서, 세 번째 직선에 둘 다 수직인 임의의 두 직선은 평행 공준(parallel postulate) 때문에 서로 평행(parallel)입니다. 반대로, 만약 한 직선이 두 번째 직선에 수직이면, 그것은 역시 해당 두 번째 직선에 평행한 임의의 직선에 수직입니다.
오른쪽 그림에서, 주황색-음영처리된 모든 각도는 서로 합동이고 초록색-음영처리된 모든 각도는 서로 합동인데, 왜냐하면 수직 각도(vertical angles)는 합동이고 횡단 절단 평행 직선에 의해 형성되는 교대하는 내부 각도는 합동이기 때문입니다. 그러므로, 만약 직선 a와 b가 평행이면, 다음 결론 중 임의의 하나가 다른 것들 모두로 이어집니다:
- 다이어그램에서 각도 중 하나는 직각입니다.
- 주황색-음영처리된 각도 중 하나는 초록색-음영처리된 각도 중 하나와 합동입니다.
- 직선 c는 직선 a와 수직입니다.
- 직선 c는 직선 b와 수직입니다.
In computing distances
한 점에서 직선까지의 거리(distance from a point to a line)는 해당 직선 위에 가장 가까운 점까지의 거리입니다. 즉 그것에서 주어진 점까지의 선분이 직선에 수직인 점입니다.
마찬가지로, 한 점에서 곡선(curve)까지의 거리는 곡선 위에 가장 가까운 점에서 곡선에 대한 접선(tangent line)에 수직인 선분으로 측정됩니다.
수직 회귀(perpendicular regression)는 데이터 점에서 직선까지의 수직 거리의 제곱의 합을 최소화함으로써 직선을 데이터 점에 맞춥니다.
한 점에서 평면까지의 거리(distance from a point to a plane)는 평면에 수직인 선분을 따라 그 점에서 선분으로 측정되며, 그것은 평면에서 주어진 점까지 가장 가까운 점을 통과하는 평면에서 모든 직선에 수직임을 의미합니다.
Graph of functions
이-차원 평면에서, 직각은 만약 두 직선의 기울기(slopes)의 곱(product)이 −1과 같으면 둘의 교차된 직선에 의해 형성될 수 있습니다. 따라서 둘의 선형 함수(linear function): \(y_1=a_1 x+b_1\)과 \(y_2=a_2 x +b_2\)을 정의하면, 함수의 그래프가 만약 \(a_1a_2=-1\)이면 수직일 것이고 직선이 교차하는 넷의 직각을 만들 것입니다. 어쨌든, 이 방법은 만약 기울기가 영 또는 정의되지 않으면 (그 직선이 축에 평행하면) 사용될 수 없습니다.
또 다른 방법에 대해, 둘의 선형 함수를: \(a_1x+b_1y+c_1=0\)와 \(a_2x+b_2y+c_2=0\)라고 놓습니다. 직선은 수직이 될 것과 \(a_1a_2+b_1b_2=0\)인 것은 필요충분 조건입니다. 이 방법은 벡터(vector)의 점 곱(dot product) (또는, 보다 일반적으로, 안의 곱(inner product))에서 단순화됩니다. 특히, 두 벡터는 만약 그것들의 안의 곱이 영이면 직교로 고려됩니다.
In circles and other conics
Circles
원(circle)의 각 지름(diameter)은 지름이 원과 교차하는 점에서 해당 원에 대한 접선(tangent line)에 수직입니다.
현(chord)을 이등분하는 원의 중심을 통과하는 선분은 현에 수직입니다.
만약 임의의 둘의 수직 현의 교차점이 한 현을 길이 a와 b로 나누고 나머지 다른 현을 길이 c와 d로 나누면, \(a^2+b^2+c^2+d^2\)은 지름의 제곱과 같습니다.
주어진 점에서 교차하는 임의의 둘의 수직 현의 제곱된 길이의 합은 같은 점에서 교차하는 임의의 다른 둘의 수직 현의 길이와 같고, \(8r^2-4p^2\)에 의해 제공됩니다 (여기서 r은 원의 반지름이고 p는 중심 점에서 교차점까지의 거리입니다).
탈레스의 정리(Thales' theorem)는 원 위의 같은 점을 통과하고 지름의 반대쪽 끝점을 통과하는 두 직선은 모두 수직임을 말합니다. 이것은 원의 임의의 지름이 지름의 두 끝점을 제외하고 원의 임의의 점에서 직각에 끼워진다고 말하는 것과 동등합니다.
Ellipses
타원(ellipse)의 주요 축과 보조 축(axes)은 서로 수직이고 축이 타원과 교차하는 점에서 타원의 접선에 대해 수직입니다.
타원의 주요 축은 방향선(directrix)과 각 래투스 렉텀(latus rectum)에 수직입니다.
Parabolas
포물선(parabola)에서, 대칭의 축은 축이 포물선과 교차하는 점에서 래투스 렉텀, 방향선, 및 접선 각각에 수직입니다.
접선 위의 한 점에서 포물선의 꼭짓점까지의, 포물선에 대한 다른 접선은 해당 점에서 포물선의 초점(focus)을 통과하는 직선에 수직입니다.
포물선의 직교 속성(orthoptic property)은 만약 포물선에 대한 두 접선이 서로 수직이면, 그것들은 방향선 위에서 교차한다는 것입니다. 반대로, 방향선 위에서 교차하는 두 접선은 수직입니다. 이것은, 그것의 방향선 위의 임의의 점에서 보인, 임의의 포물선이 직각에 끼워진다는 것을 의미합니다.
Hyperbolas
쌍곡선(hyperbola)의 횡단 축(transverse axis)은 켤레 축과 각 방향선에 수직입니다.
쌍곡선 위에 또는 그것의 켤레 쌍곡선 위의 점 P에서 점근선까지의 수직 거리의 곱은 P의 위치와 독립적인 상수입니다.
직각 쌍곡선(rectangular hyperbola)은 서로 수직인 점근선(asymptote)을 가집니다. 그것은 \(\sqrt{2}\)와 같은 이심률(eccentricity)을 가집니다.
In polygons
Triangles
직각 삼각형(right triangle)의 다리는 서로 수직입니다.
삼각형(triangle)의 고도(altitudes)는 그것들 각각의 밑변(bases)에 수직입니다. 변의 수직 이등분선(perpendicular bisector)은 역시 삼각형 기하학에서 중요한 역할을 합니다.
이등변 삼각형(isosceles triangle)의 오일러 직선(Euler line)은 삼각형의 밑변에 수직입니다.
드로즈-파니 직선 정리(Droz-Farny line theorem)는 삼각형의 직교중심(orthocenter)에서 교차하는 두 수직 직선의 속성에 관한 것입니다.
하코트의 정리(Harcourt's theorem)는 꼭짓점(vertex)을 통과하는 선분과 삼각형의 내원(incircle)에 접하는(tangent) 임의의 직선에 수직인 관계에 관한 것입니다.
Quadrilaterals
정사각형(square) 또는 다른 직사각형(rectangle)에서, 모든 인접한 변의 쌍은 수직입니다. 직각 사다리꼴(right trapezoid)은 수직인 두 쌍의 인접한 변을 갖는 사다리꼴(trapezoid)입니다.
사변형(quadrilateral)의 네 적도(maltitude) 각각은 반대쪽 변의 중간점(midpoint)을 통과하는 한 변에 수직입니다.
직교-대각 사변형(orthodiagonal quadrilateral)은 그것의 대각선(diagonal)이 수직인 사변형입니다. 이것들은 정사각형(square), 마름모(rhombus), 및 연(kite)을 포함합니다. 브라마굽타의 정리(Brahmagupta's theorem)에 의해, 역시 순환(cyclic)인 직교-대각 사변형에서, 한 변의 중간점과 대각선의 교차 점을 통과하는 직선은 반대쪽 변에 수직입니다.
판 오벨의 정리(van Aubel's theorem)에 의해, 만약 정사각형이 사변형의 변 위에 외부적으로 구성되면, 반대쪽의 정사각형의 중심을 연결하는 선분은 수직이고 길이에서 같습니다.
Lines in three dimensions
삼차원 데카르트 좌표 시스템(Cartesian coordinate system)의 x, y, 및 z축으로 예시된 것처럼, 삼-차원 공간(three-dimensional space)에서 최대 셋의 직선이 쌍별로 수직일 수 있습니다.
External links
- Definition: perpendicular with interactive animation.
- How to draw a perpendicular bisector of a line with compass and straight edge (animated demonstration).
- How to draw a perpendicular at the endpoint of a ray with compass and straight edge (animated demonstration).


