본문 바로가기
영문 위키피디아 번역

(번역) Mathematical proof

by 다움위키 2023. 11. 19.

수학적 증명(mathematical proof)은 수학적 명제(mathematical statement)에 대한 추론적(inferential) 논증(argument)으로, 말했던 가정이 논리적으로 결론을 보장한다는 것을 보이는 것입니다. 논증(argument)은, 정리(theorems)와 같은, 다른 이전에 설립된 명제를 사용할 수 있습니다; 그러나 모든 각 증명은, 원칙적으로, 추론(inference)의 인정된 규칙과 함께, 공리(axiom)로 알려진, 특정 기본 또는 원래 가정을 오직 사용하여 구성될 수 있습니다. 증명은 논리적 확실성을 수립하는 철저한 연역적 추론(deductive reasoning)의 예제이며, "합리적인 기대"를 수립하는 경험적(empirical) 논증 또는 비-철저한 귀납적 추론(inductive reasoning)과 구별되는 것입니다. 명제가 유지하는 많은 경우를 제시하는 것은 증명에 대해 충분하지 않으며, 증명은 명제가 모든 가능한 경우에서 참임을 반드시 시연해야 합니다. 참이 되는 것으로 믿어지는 입증되지-않은 제안은, 만약 추후의 수학적 연구에 대해 가정으로 자주 사용되면, 추측(conjecture) 또는 가설로 알려져 있습니다.

증명은, 보통 일부 모호성을 인정하는 자연 언어(natural language)와 함께, 수학적 기호에서 표현된 논리(logic)를 사용합니다. 대부분의 수학적 문헌에서, 증명은 엄격한 비공식 논리(informal logic)의 관점에서 쓰입니다. 자연 언어의 참여 없이 기호적 언어(symbolic language)로 완전히 쓰인, 순수하게 형식적 증명(formal proof)은 증명 이론(proof theory)에서 고려됩니다. 형식적 및 비-형식적 증명(formal and informal proofs) 사이의 구별은 현재와 역사적 수학적 실습(mathematical practice), 수학에서 준-경험론(quasi-empiricism in mathematics), 및 이른바 통속 수학(folk mathematics), 주류 수학 공동체 또는 다른 문화에서 구두 전통에 대한 많은 연구로 이어져 왔습니다. 수학의 철학(philosophy of mathematics)은 언어의 역할과 증명에서 논리, 및 언어로 수학(mathematics as a language)과 관련됩니다.

History and etymology

단어 "proof"은 라틴어 probare (테스트하는 것)에서 나옵니다. 관련된 현대 단어는 영어 "probe", "probation", 및 "probability", 스페인어 probar (냄새 맡는 것 또는 맛보는 것, 또는 때때로 만지는 것 또는 테스트하는 것), 이탈리아어 provare (시도하는 것), 및 독일어 probieren (시도하는 것)입니다. 법률상의 용어 "probity"는 평판 또는 지위가 사람에 의해 주어졌을 때, 사실을 입증하기 위한 권위 또는 신뢰성, 증언의 힘을 의미합니다.

그림 및 유추와 같은 휴리스틱 장치를 사용하여 타당성 논증은 엄격한 수학적 증명보다 선행되었습니다. 결론을 시연하는 아이디어가 토지 측량의 실질적인 문제에 기원을 둔, 기하학(geometry)과 연결에서 처음으로 생겼을 가능성이 있습니다. 수학적 증명의 개발은 주로 고대 그리스 수학(ancient Greek mathematics)의 생산물이고, 그것의 가장 큰 성과 중 하나입니다. 탈레스(Thales) (기원전 624–546) 및 키오스의 히포크라테스(Hippocrates of Chios) (기원전 c. 470–410)는 기하학에서 정리의 최초의 알려진 증명을 제공했습니다. 에우독소스(Eudoxus) (기원전 408–355) 및 테아이테토스(Theaetetus) (기원전 417–369)는 정리를 공식화했지만 그것을 증명하지는 못했습니다. 아리스토텔레스(Aristotle) (기원전 384–322)는 정의는 이미 알려진 다른 개념의 관점에서 정의되는 개념을 설명해야 한다고 말했습니다.

수학적 증명은 오늘날에도 여전히 사용되고 있는 공리적 방법(axiomatic method)을 도입한 유클리드(Euclid) (300 BCE)에 의해 혁신되었습니다. 그것은 비-정의된 용어(undefined term)와 공리(axioms), 자체-분명히 참인 것으로 가정되는 비-정의된 용어와 관련된 제안으로 시작합니다 (그리스어 "axios", 가치 있는 것). 이 기초로부터, 그 방법은 연역적 논리(deductive logic)를 사용하여 정리를 증명합니다. 유클리드의 책, 원론(Elements)은 20 세기 중반까지 서양에서 교육받은 것으로 여겨지는 사람들에 의해 읽혔습니다. 피타고라스의 정리(Pythagorean theorem)와 같은 기하학의 정리 외에도, 원론은 2의 제곱근이 무리수라는 증명과 무한하게 많은 소수가 있다는 증명을 포함하는 숫자 이론을 역시 다룹니다.

뒤따른 발전은 역시 중세 이슬람 수학(medieval Islamic mathematics)에서 자리 잡았습니다. 초기 그리스 증명은 크게 기하학적 시연이었지만, 이슬람 수학자에 의한 산술(arithmetic)과 대수(algebra)의 발달은 기하학적 직관에 의존하지 않는 보다 일반적인 증명을 허용했습니다. 기원후 10세기에서, 이라크(Iraqi) 수학자 알-헤시미(Al-Hashimi)는 무리수(irrational number)의 존재를 포함하여 곱셈, 나눗셈 등에 관한 대수적 제안을 입증하기 위해, "직선"이라고 불리지만 기하학적 대상의 측정으로 필연적으로 여겨질 수 없는 숫자들과 함께 연구했습니다. 산술 수열(arithmetic sequences)에 대해 귀납적 증명(inductive proof)은 알 카라지(Al-Karaji)에 의해 Al-Fakhri (1000)에서 도입되었으며, 그는 이항 정리(binomial theorem)와 파스칼의 삼각형(Pascal's triangle)의 속성을 증명하기 위해 그것을 사용했습니다. 알하젠(Alhazen)은 유클리드(Euclidean) 평행 공준(parallel postulate)을 증명하기 위한 첫 번째 시도로서 모순에 의한 증명(proof by contradiction)의 방법을 개발했습니다.

현대의 증명 이론(proof theory)은, 공리가 어떤 의미에서든 "참"이라는 가정을 요구하지 않는, 귀납적으로 정의된 데이터 구조(data structure)로 증명을 취급합니다. 이것은 대안적인 공리의 집합, 예를 들어 공리적 집합 이론(Axiomatic set theory) 및 비-유클리드 기하학(Non-Euclidean geometry)을 기반으로, 주어진 직관적 개념의 형식적 모델로 평행 수학적 이론을 허용합니다.

Nature and purpose

행할 때, 증명은 자연 언어로 표현되고 청중에게 명제의 진리를 확신시키기 위한 엄격한 주장입니다. 엄격함의 기준은 절대적이지 않고 역사를 관통하여 변화해 왔습니다. 증명은 의도된 청중에 따라 다르게 제시될 수 있습니다. 수락을 얻기 위해, 증명은 엄격함의 공동의 표준을 충족시켜야 합니다; 모호하거나 불완전한 것으로 여겨지는 논증(argument)은 거부될 수 있습니다.

증명의 개념은 수학적 논리의 분야에서 공식화됩니다. 형식적 증명(formal proof)은 자연 언어 대신에 형식적 언어(formal language)로 쓰입니다. 형식적 증명은 가정, 및 이전 공식의 논리적 결과인 후속 공식으로 시작하여, 형식적 언어에서 공식의 수열입니다. 이 정의는 증명의 개념을 연구하기에 적합하게 만듭니다. 실제로, 증명 이론(proof theory)의 분야는 형식적 증명과 그것의 속성을 연구하는데, 거의 모든 공리적 시스템에 있는 가장 유명하고 놀라운 것은 시스템 이내에서 입증할 수 없는 특정 결정-불가능한 명제(undecidable statements)를 생성할 수 있습니다.

형식적 증명의 정의는 수학의 실습에서 쓰인 증명의 개념을 포착하기 위해 의도됩니다. 이 정의의 건전성은 출판된 증명이, 원칙적으로, 형식적 증명으로 변환될 수 있다는 믿음에 이릅니다. 어쨌든, 자동화된 증명 보조도구(proof assistant)의 분야 밖에서, 이것은 실제로 거의 이루어지지 않습니다. 철학에서 고전적 질문은 수학적 증명이 분석적(analytic) 또는 종합적(synthetic)인지 여부를 묻는 것입니다. 분석-합성적 구별(analytic–synthetic distinction)을 도입한 칸트(Kant)는 수학 증명이 종합적이라고 믿었지만, 콰인(Quine)은 1951년 "Two Dogmas of Empiricism"에서 그러한 구별이 보유할 수 없다고 주장했습니다.

증명은 그들의 수학적 아름다움(mathematical beauty)에 대해 존경받을 수 있습니다. 수학자 폴 에르되시(Paul Erdős)는 각 이론을 입증하는 가장 아름다운 방법을 포함하는 가상의 고서, "The Book"에서 나올 때 특히 우아한 것으로 밝혀졌다는 것으로 증명을 묘사한 것에 대해 알려져 있습니다. 2003년에 출판된, 책 Proofs from THE BOOK은 편집자들이 특히 기쁘게 생각하는 32 증명을 제시하는 데 사용됩니다.

Methods

Direct proof

직접적 증명에서, 그 결론은 공리, 정의, 및 초기 정리를 논리적으로 결합함으로써 확립됩니다. 예를 들어, 직접적 증명은 두 짝수(even) 정수(integer)의 합이 항상 짝수임을 증명하기 위해 사용될 수 있습니다:

  • 두 짝수 정수 x 및 y를 생각해 보십시오. 그들이 짝수이므로, 그들은 정수 a와 b에 대해, 각각, x = 2a 및 y = 2b로 쓰일 수 있습니다. 그런-다음 합 x + y = 2a + 2b = 2(a+b)입니다. 그러므로 x+y는 인수로 2를 가지고, 정의에 의해, 짝수입니다. 따라서, 임의의 두 짝수 정수의 합은 짝수입니다.

이 증명은 짝수 정수의 정의, 덧셈 및 곱셈 아래에서 클로저(closure)의 정수 속성 및 분배성(distributivity)을 사용합니다.

Proof by mathematical induction

그것의 이름에도 불구하고, 수학적 귀납법은 귀납적 추론(inductive reasoning)의 형식이 아니라 연역법(deduction)의 방법입니다. 수학적 귀납법에 의한 증명에서, 단일 "기본 경우"가 입증되고, "귀납법 규칙"은 어떤 임의의 경우가 다음 경우를 의미(implies)하는 것으로 설립하는 것으로 입증됩니다. 원칙적으로 귀납법 규칙은 반복적으로 적용될 수 있으므로 (증명된 기본 경우로부터 시작하여), 모든 (보통 무한하게(infinitely) 많은) 경우가 입증될 수 있음이 따릅니다. 이것은 개별적으로 각 경우를 입증하는 것을 피합니다. 수학적 귀납법의 변형은 무한 하강에 의해 증명(proof by infinite descent)이며, 이것은, 예를 들어, 2의 제곱근의 무리수성(irrationality of the square root of two)을 입증하기 위해 사용될 수 있습니다.

수학적 귀납법에 의한 증명의 공통적인 적용은 하나의 숫자에 대해 유지되는 것으로 알려진 속성이 모든 자연수에 대해 유지된다는 것을 증명하는 것입니다: N = {1,2,3,4,...}을 자연수의 집합으로 놓고, P(n)을 다음을 만족하는 N에 속하는 자연수 n을 포함하는 수학적 명제로 놓습니다:

  • (i) P(1)가 참입니다, 즉, P(n)은 n = 1에 대해 참입니다.
  • (ii) P(n+1)은 P(n)가 참일 때마다 참입니다, 즉, P(n)이 참인 것은 P(n+1)이 참인 것을 의미합니다.
  • 그런-다음 P(n)은 모든 자연수 n에 대해 참입니다.

예를 들어, 우리는 형식 2n − 1의 모든 양의 정수가 홀수임을 귀납법에 의해 증명할 수 있습니다. P(n)이 "2n − 1이 홀수"임을 나타내는 것으로 놓습니다:

  • (i) n = 1에 대해, 2n − 1 = 2(1) − 1 = 1이고, 1은 홀수인데, 왜냐하면 그것은 2로 나누었을 때 1의 나머지를 남기기 때문입니다. 따라서 P(1)은 참입니다.
  • (ii) 임의의 n에 대해, 만약 2n − 1이 홀수이면 (P(n)이면), (2n − 1) + 2은 역시 반드시 홀수인데, 왜냐하면 홀수에 2를 더하는 것은 홀수를 초래하기 때문입니다. 그러나 (2n − 1) + 2 = 2n + 1 = 2(n+1) − 1이므로, 2(n+1) − 1입니다 (P(n+1)입니다). 그래서 P(n)은 P(n+1)임을 의미합니다.
  • 따라서 모든 양의 정수 n에 대해, 2n − 1가 홀수입니다.

더 짧은 어구 "귀납법에 의해 증명"은 종종 "수학적 귀납법에 의한 증명" 대신에 사용됩니다.

Proof by contraposition

대우에 의한 증명(Proof by contraposition)은 논리적으로 동등한 대우(contrapositive) 명제: "만약 q가 아니면 p가 아닙니다"를 설립함으로써 명제 "만약 p이면 q입니다"를 추론(infers)합니다.

예를 들어, 대우는, 정수 \(x\)가 주어지면, 만약 \( x^2 \)가 짝수이면, \(x\)가 짝수임을 설립하기 위해 사용될 수 있습니다:

  • \(x\)가 짝수가 아님을 가정합니다. 그런-다음 \(x\)가 홀수입니다. 두 홀수의 곱은 홀수이며, 따라서 \( x^2  = x\cdot x \)는 홀수입니다. 따라서 \( x^2 \)는 짝수가 아닙니다. 따라서, 만약 \( x^2 \)가 짝수이면, 가정은 틀림없이 거짓이며, 따라서 \(x\)는 짝수여야 합니다.

Proof by contradiction

라틴어 문구 reductio ad absurdum (귀류법)으로 역시 알려진 모순에 의한 증명에서, 만약 어떤 명제가 참이라고 가정되면, 논리적 모순이 발생하며, 따라서 그 명제가 거짓이어야 함을 알 수 있습니다. 유명한 예제는 \(\sqrt{2}\)가 무리수(irrational number)라는 증명을 포함합니다:

  • \(\sqrt{2}\)가 유리수라고 가정합니다. 그런-다음 \(\sqrt{2} = {a\over b}\)로 가장-낮은 항으로 쓰일 수 있으며, 여기서 a와 b는 공통 인수 없는(no common factor) 비-영 정수입니다. 따라서, \(b\sqrt{2} = a\)입니다. 양변을 제곱하면 \(2b^2=a^2\)을 산출합니다. 2는 왼쪽 변에 대한 표현을 나누므로, 2는 오른쪽 변에 대한 같은 표현을 역시 나누어야 합니다. 즉, \(a^2\)은 짝수이며, 여기서 위의 제안에서 보이듯이 (대우에 의한 증명에서), 역시 짝수여야 함을 의미합니다. 따라서 우리는 \(a=2c\)를 쓸 수 있으며, 여기서 \(c\)는 역시 정수입니다. 원래 방정식으로 대체하면 \(2b^2=(2c)^2=4c^2\)을 산출합니다. 양쪽변을 2로 나누면 \(b^2 = 2c^2\)을 산출합니다. 그러나 그런-다음, 이전처럼 같은 논증에 의해, 2는 \(b^2\)을 나누므로, \(b\)는 짝수여야 합니다. 어쨌든, 만약 \(a\)와 \(b\)가 둘 다 짝수이면, 그들은 공통 인수로 2를 가집니다. 이것은 \(a\)와 \(b\)가 공통 인수를 가지지 않는다는 이전 명제에 모순되므로, 우리는 \(\sqrt{2}\)는 무리수라는 결론 내림을 강제합니다.

쉬운 말로: 만약 우리가 \(\sqrt{2}\)를 분수로 쓸 수 있으면, 이 분수는 절대 가장-낮은 항에서 절대 쓰일 수 없는데, 왜냐하면 2는 분자와 분모에서 항상 인수화 될 수 있기 때문입니다.

Proof by construction

구성에 의한 증명, 또는 예제에 의한 증명은 해당 속성을 가진 무언가가 존재함을 보이기 위해 속성을 가진 구체적인 예제의 구성입니다. 조제프 리우빌(Joseph Liouville)은, 예를 들어, 명백한 예제(explicit example)를 구성함으로써 초월적 숫자(transcendental number)의 존재를 증명했습니다. 그것은 역시 모든 원소가 특정 속성을 가진다는 제안을 반증하기 위해 반대-예제(counterexample)를 구성하기 위해 사용할 수 있습니다.

Proof by exhaustion

소진에 의한 증명에서, 그 결론은 그것을 유한 숫자의 경우로 나누고 개별적으로 각각의 경우를 입증함으로써 설립됩니다. 경우의 숫자는 때때로 매우 커지게 될 수 있습니다. 예를 들어, 네 가지 색깔 정리(four color theorem)의 첫 번째 증명은 1,936 경우를 갖는 소진에 의한 증명이었습니다. 이 증명은 논쟁의-여지가 있는데 왜냐하면 대부분의 경우가 수작업이 아닌 컴퓨터 프로그램에 의해 확인되었기 때문입니다. 2011년 당시 네 가지 색깔 정리의 가장-짧은 알려진 증명은 여전히 600개가 넘는 경우를 가집니다.

Probabilistic proof

확률적 증명은 예제가, 확률 이론(probability theory)의 방법을 사용함으로써, 확실성과 함께, 존재하는 것을 보여주는 것입니다. 구성에 의한 증명과 같은, 확률적 증명은 존재 이론(existence theorem)을 보여주기 위한 많은 방법 중 하나입니다.

확률적 방법에서, 우리는 주어진 속성을 가진 대상을 찾으며, 후보의 큰 집합으로 시작합니다. 우리는 선택하려는 각 후보에 대해 특정 확률을 할당하고, 그런-다음 선택한 후보가 원하는 속성을 가질 비-영 확률이 있음을 증명합니다. 이것은 후보가 속성을 가짐을 지정하는 것이 아니라, 확률이 적어도 하나 없이 양수일 수 없습니다.

확률론적 증명은 정리가 '아마도' 참, '타당성 논증'이라는 논증과 혼동되어서는 안 됩니다. 콜라츠 추측(Collatz conjecture)에 대한 연구는 타당성이 진짜 증명으로부터 얼마나 멀리 떨어져 있는지 보여줍니다. 반면에 대부분의 수학자들은 주어진 대상의 속성에 대해 확률적 증거가 진정한 수학적 증거로 생각하지 않지만, 몇몇 수학자와 철학자들은 (소수성을 테스트하는 것에 대해 라빈의 확률적 알고리듬(probabilistic algorithm)과 같은) 적어도 일부 유형의 확률적 증거가 진짜 수학적 증명만큼 좋은 것임을 주장했습니다.

Combinatorial proof

조합적 증명은 그들이 같은 대상을 다른 표현에서 세는 것을 보여줌으로써 다른 표현의 동등성을 확립합니다. 종종 두 집합 사이의 전단사(bijection)가 그들의 두 크기에 대해 표현이 같다는 것을 보여주기 위해 사용됩니다. 대안적으로, 이중 셈 논증(double counting argument)은 단일 집합의 크기에 대해 두 다른 표현을 제공하여, 두 표현이 같음을 다시 보입니다.

Nonconstructive proof

 

비-구성적 증명은 – 그러한 대상이 찾아지는 방법을 설명 없이 – 특정 속성을 가진 수학적 대상(mathematical object)이 존재함을 확립합니다. 종종, 이것은 대상의 비-존재가 불가능임을 입증되는 것에서 모순에 의한 증명의 형식을 취합니다. 대조적으로, 구성적인 증명은 특정 대상이 그것을 찾는 것의 방법을 제공함으로써 존재한다는 것을 확립합니다. 비-구성적 증명의 유명한 예제는 \(a^b\)가 유리수(rational number)임을 만족하는 두 무리수(irrational number) a와 b가 존재함을 보입니다:

  • \(\sqrt{2}^{\sqrt{2}}\)가 유리수이고 우리가 행하는 것 (\(a=b=\sqrt{2}\)을 취하면), 또는 \(\sqrt{2}^{\sqrt{2}}\)가 무리수이므로 우리는 \(a=\sqrt{2}^{\sqrt{2}}\)와 \(b=\sqrt{2}\)을 쓸 수 있는 것 중 하나입니다. 이것은 그런-다음 \(\left (\sqrt{2}^{\sqrt{2}}\right )^{\sqrt{2}}=\sqrt{2}^{2}=2\)을 제공하며, 이것은 따라서 형식 \(a^b\)의 유리수입니다.

Statistical proofs in pure mathematics

표현 "통계적 증명"은 암호화(cryptography), 혼돈 급수(chaotic series), 및 확률적 또는 해석적 숫자 이론(number theory)을 포함하는 것과 같은 순수 수학(pure mathematics)의 영역에서 기술적으로 또는 구어체적으로 사용될 수 있습니다. 수학적 통계학(mathematical statistics)으로 알려진 수학의 가지에서 수학적 증명을 참조하기 위해 덜 공통적으로 사용됩니다. 아래의 "데이터를 사용하여 통계적 증명(Statistical proof using data)" 섹션을 역시 참조하십시오.

Computer-assisted proofs

20세기까지, 원칙적으로 임의의 증명은 유능한 수학자에 의해 그것의 유효성을 확인하기 위해 검사될 수 있다고 가정되었습니다. 어쨌든, 컴퓨터는 이제 이론을 입증하는 것과 검사하기 위해 임의의 인간 또는 인간의 팀에 대해 너무 긴 계산을 수행하는 것 둘 다에 이제 사용됩니다; 네 가지 색깔 정리(four color theorem)의 첫 번째 증명은 컴퓨터-보조 증명의 예제입니다. 일부 수학자들은 컴퓨터 프로그램에서 오류 또는 계산에서 실행-시간 오류의 가능성은 컴퓨터-보조 증명의 유효성을 문제로 호출합니다. 실제에서, 컴퓨터-보조 증명을 무효화하는 오류의 가능성이 중복과 자체-검사를 계산에 통합하고, 여러 독립적 접근과 프로그램을 개발함으로써 줄어들 수 있습니다. 오류는 특히 만약 증명이 자연 언어를 포함하고 잠재적 숨겨진 숨겨진 가정과 포함된 결점을 발견하기 위해 깊은 수학적 통찰력이 요구되면, 사람에 의한 증명의 검증의 경우에서 절대 완전히 배제될 수 없습니다.

Undecidable statements

공리의 집합으로부터 증명-가능도 아니고 비-증명가능도 아닌 명제는 (그들의 공리들로부터) 비-결정가능한 것으로 불립니다. 하나의 예제는 평행 공준(parallel postulate)이며, 이것은 유클리드 기하학(Euclidean geometry)의 남아있는 공리로부터 증명-가능도 아니고 비-증명가능도 아닙니다.

수학자들은 체르멜로–프렝켈 집합 이론(Zermelo–Fraenkel set theory)에서 선택의 공리 (ZFC), 수학에서 집합 이론의 표준 시스템 (ZFC가 일관된 것임을 가정)에서 증명-가능도 아니고 비-증명가능도 아닌 많은 명제가 있음을 보여 왔습니다; ZFC에서 비-결정가능한 명제 목록을 참조하십시오.

괴델의 (첫 번째) 불완전성 정리(Gödel's (first) incompleteness theorem)는 많은 수학적 흥미의 공리 시스템이 비-결정가능한 명제를 가질 것임을 보입니다.

Heuristic mathematics and experimental mathematics

크니도스의 에우독소스(Eudoxus of Cnidus)와 같은 초기 수학자들은, 유클리드에서 19세기 후반과 20세기의 기초 수학(foundational mathematics) 개발까지 증명을 사용하지 않았지만, 증명은 수학의 필수적인 부분이었습니다. 1960년대에서 컴퓨팅 능력이 증가와 함께, 중요한 연구는 실험 수학(experimental mathematics)에서 증명-정리 프레임워크 외부의 수학적 대상(mathematical objects)을 조사하는 것을 행하는 것으로 시작되었습니다. 이들 방법의 초기 개척자들은 궁극적으로 연구를 고전적인 증명-정리 프레임워크, 즉, 궁극적으로 그렇게 삽입되었던, 프랙탈 기하학(fractal geometry)의 초기 개발에서 삽입되는 것을 의도했습니다.

Related concepts

Visual proof

비록 형식적 증명은 아닐지라도, 수학적 정리의 시각적 시연은 "단어 없는 증명(proof without words)"이라고 때때로 불립니다. 아래의 왼쪽-편 그림은 (3,4,5) 삼각형의 경우에서 피타고라스 정리(Pythagorean theorem)의 역사적인 시각적 증명의 예제입니다.

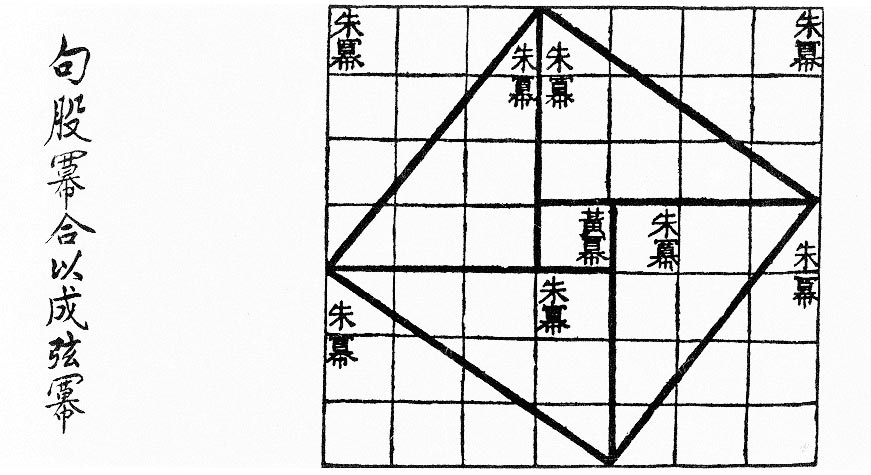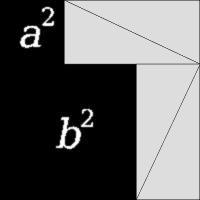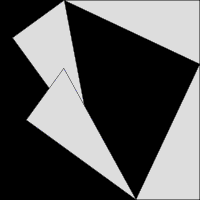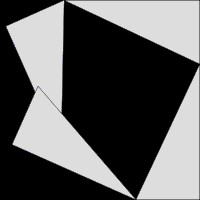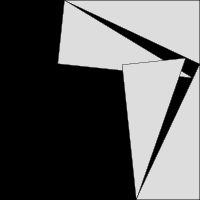잃어버린 정사각형 퍼즐(missing square puzzle)과 같은, 일부 현혹하는 시각적 증명은 가정된 수학적 사실을 증명하는 것으로 보이지만 작은 오류 (예를 들어, 아마 실제로 약간 구부러진 직선)의 존재 아래에서 오직 그렇게 되는 방법에서 구성될 수 있으며, 이것은 전체 그림이 정확하게 측정된 또는 계산된 길이와 각도와 함께 면밀히 검사 될 때까지 눈에 띄지 않습니다.

Elementary proof

기본 증명은 오직 기본 기술을 사용하는 증명입니다. 보다 구체적으로, 그 용어는 복소 해석학(complex analysis)을 사용하지 않는 증명을 참조하기 위해 숫자 이론(number theory)에서 사용됩니다. 얼마 동안 소수 정리(prime number theorem)와 같은 특정 정리는 "더 높은" 수학을 사용하여 오직 증명될 수 있다고 생각되었습니다. 어쨌든, 시간이 지남에 따라, 이들 결과 중 많은 것이 오직 기본 기술을 사용하여 다시-입증되어 왔습니다.

Two-column proof

두 평행 열을 사용하여 증명을 조직하는 특정 방법은 미국에서 기본 기하학 수업에서 종종 사용됩니다. 그 증명은 두 열에서 일련의 줄로 작성됩니다. 각 줄에서, 왼-쪽 열은 제안을 포함하며, 반면에 오른쪽 열은 왼쪽 열에서 해당하는 제안이 공리, 가설 또는 이전 제안에서 논리적으로 도출되는 방법의 간략한 설명을 포함합니다. 왼쪽 열은 전형적으로 "명제"를 향하게 되고 오른쪽 열은 전형적으로 "이유"입니다.

Colloquial use of "mathematical proof"

표현 "수학적 증명"은 일반 사람들에 의해 수학적 방법을 사용하여 또는 숫자와 같은 수학적 대상(mathematical objects)을 일상생활에 대한 어떤 것을 시현하기 위해, 또는 논증에서 사용된 데이터가 수치적일 때, 논쟁함으로써 참조하기 위해 사용됩니다. 특히 데이터(data)로부터 논쟁하기 위해 사용될 때, "통계적 증명" (아래)을 의미하기 위해 때때로 역시 사용됩니다.

Statistical proof using data

데이터로부터 "통계적 증명"은 데이터(data)의 확률(probability)에 관한 제안을 추론하기 위해 통계학(statistics), 데이터 해석(data analysis), 또는 베이즈 해석(Bayesian analysis)을 응용을 참조합니다. 통계에서 이론을 확립하기 위해 수학적 증명을 사용하는 반면에, 보통 확률 명제가 도출되는 가정은 검증하기 위한 외부 수학으로부터 경험적 증거를 요구하는 것에서 수학적 증명은 아닙니다. 물리학(physics)에서, 통계적 방법 외에도, "통계적 증명"은 입자 물리학(particle physics) 실험(experiment)에서 데이터 또는 물리적 우주론(physical cosmology)에서 관측 연구(observational study)를 분석하기 위한 적용된 특수한 물리학의 수학적 방법(mathematical methods of physics)을 참조할 수 있습니다. "통계적 증명"은, 데이터 또는 다이어그램이 추가 분석 없이 적절하게 설득될 때, 흩뜨림 그림(scatter plot)과 같은 원시 데이터 또는 데이터를 포함하는 설득력-있는 다이어그램을 역시 참조할 수 있습니다.

Inductive logic proofs and Bayesian analysis

귀납적 논리(inductive logic)를 사용하는 증명은, 본성에서 수학적으로 여겨지지만, 확률(probability)과 유사한 방법으로 작용하고, 완전 확실성(certainty)보다 작을 수 있는 확실성의 정도를 갖는 제안을 설립하려고 합니다. 귀납적 논리는 수학적 귀납법(mathematical induction)과 절대 혼동해서는 안됩니다.

베이즈 해석은 베이즈의 정리(Bayes' theorem)를 새로운 증거(evidence) 또는 정보(information)가 획득될 때 사람의 가설의 가능성의 평가(assessment of likelihoods)를 업데이트하기 위해 사용합니다.

Proofs as mental objects

심리학은 수학적 증명을 심리적 또는 정신적 대상으로 바라봅니다. 라이프니츠(Leibniz), 프레게(Frege), 카르나프(Carnap)와 같은 수학자이자 철학자(philosopher)는 이 견해를 다양하게 비판해 왔고 그들이 생각의 언어(language of thought)로 여겨지는 것에 대해 의미론을 개발하려고 시도했었으며, 그것에 의해 수학적 증명의 표준은 경험적 과학(empirical science)에 적용될 수 있습니다.

Influence of mathematical proof methods outside mathematics

스피노자(Spinoza)와 같은 철학자-수학자들은 공리적 방법에서 철학적 논증을 공식화하려고 시도해 왔으며, 그것에 의하여 수학적 증명 표준이 일반적인 철학에서 논증화에 적용될 수 있습니다. 다른 수학자-철학자들은 수학적 증명과 이유의 표준을 경험론 없이 사용하기 위해, 수학 외부의 명제에 도달하기 위해 노력해 왔지만, 데카르트(Descartes)의 코기토(cogito) 논증과 같은 수학적 증명에서 추론된 제안의 확실성(certainty)을 가집니다.

Ending a proof

때때로, 약어 "Q.E.D."는 증명의 끝을 나타내기 위해 쓰입니다. 이 약어는 "Quod Erat Demonstrandum"를 의미하며, 이것은 라틴어(Latin)에 대해 "이것은 증명된 것"입니다. 보다 공통적인 대안은 그것의 시조(eponym) 팔 헐모시(Paul Halmos) 후에 "툼스톤(tombstone)" 또는 "헐모시(halmos)"로 알려진, □ 또는 ∎와 같은, 정사각형 또는 직사각형을 사용하는 것입니다. 종종, "이것은 보일 것이었습니다"는 구두 표시 동안 "QED", "□", 또는 "∎"를 쓸 때 축어적으로 표현됩니다.

Further reading

External links

저작자표시 비영리 변경금지

관련글

티스토리툴바