허수(imaginary number)는, 그의 속성 \(i^2=-1\)에 의해 정의되는, 허수 단위 i에 의해 곱해진 실수(real number)로 쓰여질 수 있는 복소수입니다. 허수 bi의 제곱(square)은 −b2입니다. 예를 들어, 5i는 허수이고, 그의 제곱은 −25입니다. 영은 실수와 허수 모두로 간주됩니다.
원래 17세기에 르네 데카르트(René Descartes)에 의해 경멸적인 용어로 만들어졌고 허구적이거나 쓸모없는 것으로 여겨진, 이 개념은 오귀스탱-루이 코시(Augustin-Louis Cauchy), 레온하르트 오일러(Leonhard Euler) 및 카를 프리드리히 가우스(Carl Friedrich Gauss)의 연구에 따라 널리 받아들여졌습니다.
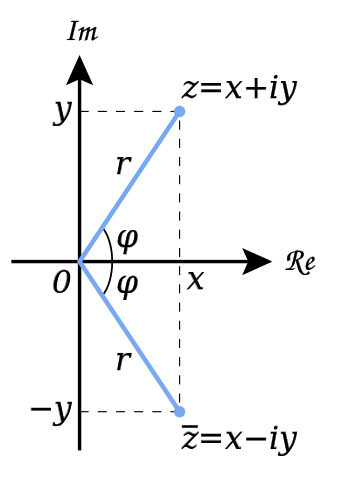
허수 bi는 실수 a에 더하여 형식 a + bi의 복소수를 형성할 수 있으며, 여기서 실수 a와 b는, 각각, 복소수의 실수 부분(real part)와 허수 부분(imaginary part)으로 불립니다.
History
비록 그리스 수학자이자 엔지니어인 알렉산드리아의 히이로(Hero of Alexandria)은 이들 숫자를 처음으로 상상한 것으로 기록되어 있을지라도, 라파엘 봄벨리(Rafael Bombelli)는 1572년에 처음으로 복소수의 곱셈에 대해 규칙을 세웠습니다. 그 개념은 이전에, 예를 들어 제롤라모 카르다노(Gerolamo Cardano)의 연구의, 출판물에서 나타났습니다. 그 당시에 음수뿐만 아니라 허수는 잘못 이해되고 일부의 사람에 의해 거짓된 것 또는 쓸모없는 것으로 여겨졌습니다. 르네 데카르트(Laren Descartes)를 포함한 다른 많은 수학자들은 허수의 사용을 채태하는 것을 느리게 했는데, 데카르트는 그의 La Géométrie에서 그들에 대해 썼으며, 여기서 용어 허수(imaginary)는 사용되었는데 경멸적인 것임을 의미했습니다. 허수의 사용은 레온하르트 오일러(Leonhard Euler) (1707–1783)와 카를 프리드리히 가우스(Carl Friedrich Gauss) (1777–1855)의 연구 전까지 널리 받아들여지지 않았습니다. 평면에서 점으로 복소수의 기하학적 중요성은 캐스퍼 비슬(Caspar Wessel) (1745–1818)에 의해 처음 설명되었습니다.
1843년 윌리엄 로언 해밀턴(William Rowan Hamilton)은 평면에서 허수 축의 아이디어를 쿼터니언 허수(quaternion imaginaries)의 사-차원 공간으로 확장했는데, 그것에서 차원의 세 개는 복소수 필드에서 허수에 대해 유사합니다.
다항식 링(polynomial ring)의 몫 링(quotient ring)의 개발과 함께, 허수 뒤에 있는 개념은 보다 실질적이 되었지만, 누군가는 +1의 제곱근을 가지는 테사린(tessarine)의 j와 같은 다른 허수를 역시 찾습니다. 이 아이디어는 1848년 시작하는 제임스 코클(James Cockle)의 기사에 처음 부상되었습니다.
Geometric interpretation
기하학적으로, 허수는, 허수 축을 실수 축에 수직(perpendicular)으로 표시되는 것을 허용하는, 복소 평면(complex number plane)의 수직 축 위에서 발견될 수 있습니다. 허수를 보는 한 가지 방법은, 오른쪽으로 크기에서 양으로 증가하는, 및 왼쪽으로 크기에서 음으로 증가하는, 표준 숫자 직선(number line)을 고려하는 것입니다. 이 x-축의 0에서, y-축은 올라가는 것으로 "양의" 방향으로 그려질 수 있습니다: "양의" 허수는 그런 다음 위쪽으로 크기에서 증가하고, "음의" 허수는 아래쪽으로 크기에서 증가합니다. 이 세로축은 종종 "허수 축"이라고 불리고 iℝ, \(\scriptstyle\mathbb{I}\), 또는 ℑ로 나타냅니다.
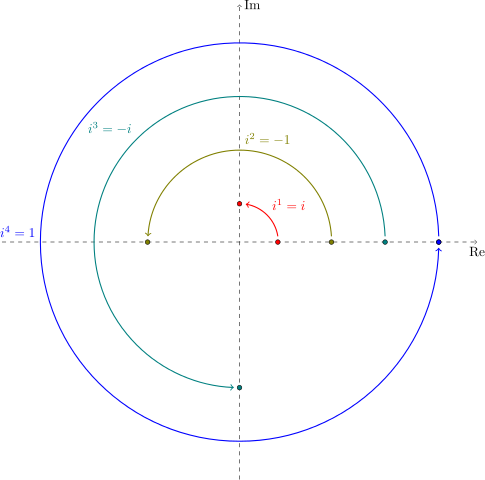
이 표현에서, –1을 곱하는 것은 원점에 대해 180도 회전(rotation)에 해당합니다. i를 곱하는 것은 "양의" 방향 (즉, 반-시계 방향)으로 90도 회전이고, 방정식 \(i^2=-1\)은 만약 우리가 원점에 대한 두 번의 90도 회전을 적용하면, 순 결과는 하나의 180도 회전하는 것을 말하는 것으로 해석할 수 있습니다. "음의" 방향 (즉, 시계 방향)으로 90도 회전은 역시 이 해석을 만족함을 주목하십시오. 이것은 −i 역시 방정식 \(x^2=-1\)의 해라는 사실을 반영합니다. 일반적으로, 복소수의 거듭제곱은 그 복소수의 편각(argument)을 원점 주위로 회전시킨 다음, 그의 크기를 스케일링하는 것과 같습니다.
Square roots of negative numbers
음수(negative number)의 제곱근(square root)의 주요 값(principal value)으로 표현된 허수와 함께 연산할 때, 주의를 기울여야 합니다. 예를 들어:
\(\quad\)\(6=\sqrt{36}=\sqrt{(-4)(-9)} \ne \sqrt{-4}\sqrt{-9} = (2i)(3i) = 6 i^2 = -6.\)
때때로 이것은 다음으로 쓰여집니다:
\(\quad\)\(-1 = i^2 = \sqrt{-1}\sqrt{-1} \stackrel{\text{ (fallacy) }}{=} \sqrt{(-1)(-1)} = \sqrt{1} = 1.\)
변수가 적절하게 제한되지 않을 때 상등 \(\sqrt{xy} = \sqrt{x}\sqrt{y}\)은 유지되지 않기 때문에, 오류(fallacy)가 발생합니다. 이 경우에서 상등은 두 숫자가 모두 음수일 때, 유지되지 않습니다. 이것은 다음과 같이 시연될 수 있습니다.
\(\quad\)\(\sqrt{-x}\sqrt{-y} = i \sqrt{x} \ i \sqrt{y} = i^2 \sqrt{x} \sqrt{y} = -\sqrt{xy} \neq \sqrt{xy},\)
여기서 두 숫자 x와 y는 비-음의 실수입니다.
Bibliography
- Nahin, Paul (1998). An Imaginary Tale: the Story of the Square Root of −1. Princeton: Princeton University Press. ISBN 0-691-02795-1., explains many applications of imaginary expressions.
External links
- How can one show that imaginary numbers really do exist? – an article that discusses the existence of imaginary numbers.
- In our time: Imaginary numbers Discussion of imaginary numbers on BBC Radio 4.
- 5Numbers programme 4 BBC Radio 4 programme
- Why Use Imaginary Numbers? Basic Explanation and Uses of Imaginary Numbers



