새로운 함수는 구할 수 있는 값을 연결해서 그래프의 변화를 그려봄으로써 그의 개형을 짐작할 수 있습니다.
삼각 함수에서 구할 수 있는 특수각의 값을 구해보면, 다음과 같습니다.
\(\quad\)\(\begin{array}{|c|cccccccc|}
\hline
\begin{matrix}\text{Radian}\\ \text{Degree}\end{matrix} &
\begin{matrix}0\\ 0^\circ\end{matrix} &
\begin{matrix}\frac{\pi}{12}\\ 15^\circ\end{matrix} &
\begin{matrix}\frac{\pi}{8}\\ 22.5^\circ\end{matrix} &
\begin{matrix}\frac{\pi}{6}\\ 30^\circ\end{matrix} &
\begin{matrix}\frac{\pi}{4}\\ 45^\circ\end{matrix} &
\begin{matrix}\frac{\pi}{3}\\ 60^\circ\end{matrix} &
\begin{matrix}\frac{5\pi}{12}\\ 75^\circ\end{matrix} &
\begin{matrix}\frac{\pi}{2}\\ 90^\circ\end{matrix} \\
\hline
\sin &
0 &
\frac{ \sqrt{6} - \sqrt{2} } {4} &
\frac{ \sqrt{2 - \sqrt{2}} } {2} &
\frac{1}{2} &
\frac{\sqrt{2}}{2} &
\frac{\sqrt{3}}{2} &
\frac{ \sqrt{6} + \sqrt{2} } {4} &
1 \\
\cos &
1 &
\frac{\sqrt{6}+\sqrt{2}}{4} &
\frac{ \sqrt{2 + \sqrt{2}} } {2} &
\frac{\sqrt{3}}{2} &
\frac{\sqrt{2}}{2} &
\frac{1}{2} &
\frac{ \sqrt{6} - \sqrt{2}} {4} &
0 \\
\tan &
0 &
2-\sqrt{3} &
\sqrt{2} - 1 &
\frac{\sqrt{3}}{3} &
1 &
\sqrt{3} &
2+\sqrt{3} &
\infty \\
\cot &
\infty &
2+\sqrt{3} &
\sqrt{2} + 1 &
\sqrt{3} &
1 &
\frac{\sqrt{3}}{3} &
2-\sqrt{3} &
0 \\
\sec &
1 &
\sqrt{6} - \sqrt{2} &
\sqrt{2} \sqrt{ 2 - \sqrt{2} } &
\frac{2\sqrt{3}}{3} &
\sqrt{2} &
2 &
\sqrt{6}+\sqrt{2} &
\infty \\
\csc &
\infty &
\sqrt{6}+\sqrt{2} &
\sqrt{2} \sqrt{ 2 + \sqrt{2} } &
2 &
\sqrt{2} &
\frac{2\sqrt{3}}{3} &
\sqrt{6} - \sqrt{2} &
1 \\\hline
\end{array}\)
이 테이블에서 길이비가 알려지지 않는 것들의 값은 삼각함수의 덧셈정리를 이용해서 구할 수 있습니다. 삼각함수에서 언급한 것처럼, 이 외에 동경의 위치가 제 2, 3, 4분면에서는 대칭이동으로 삼각 함수의 값을 평가할 수 있습니다.
사인함수 그래프

사인 함수 \(y=\sin x\)의 그래프는 위의 값을 토대로 그림처럼 그려집니다.
이 함수의 주요 특징은 다음과 같습니다.
- 정의역 : 실수 전체의 집합
- 치역 : \(\{y|-1\leq y \leq 1\}\)
- 주기 : \(2\pi\) (한 바퀴)
- 대칭 : 원점 대칭(홀수 함수)
코사인함수 그래프

코사인 함수 \(y=\cos x\)의 그래프는 위의 값을 토대로 그림처럼 그려집니다.
이 함수의 주요 특징은 다음과 같습니다.
- 정의역 : 실수 전체의 집합
- 치역 : \(\{y|-1\leq y \leq 1\}\)
- 주기 : \(2\pi\) (한 바퀴)
- 대칭 : \(y\)-축 대칭(짝수 함수)
탄젠트함수 그래프

탄젠트 함수 \(\displaystyle y=\tan x=\frac{\sin x}{\cos x}\)는 근본적으로 분수함수입니다. 분수함수는 분모가 0이 될 수 없으므로, 이 값을 정의역에서 제외해야 하고, 분모가 0으로 접근할 때, 크기가 매우 커지며, 이것이 점근선이 됩니다.
어쨌든, 위의 값과 점근선을 토대로 그럼처럼 그려지고, 주요 특징은 다음과 같습니다.
- 정의역 : \(x\neq n\pi+\frac{\pi}{2}\) (\(n\)은 정수)
- 치역 : 실수 전체의 집합
- 주기 : \(\pi\)
- 대칭 : 원점대칭(홀수 함수)
- 점근선 : \(x = n\pi+\frac{\pi}{2}\) (\(n\)은 정수)
분수함수에서 정의역에서 제외된 값들이 점근선이 될 수 있음을 잊지 마시기 바랍니다.
단위 원에서의 삼각 함수의 그래프
한편, 단위 원에서, 해당 좌표를 스크린에 비쳐보면, 그 결과가 각 함수의 그래프가 됩니다.

각 계수들의 특징
기본 그래프의 평행이동과 대칭이동, 특히 주기의 변화, 크기의 변화 등을 고려한 다음과 같은 식의 그래프를 생각해 보십시오.
- \(y=2\sin x\)는 치역만 2배로 늘어납니다.
- \(y=\sin 2x\)는 주기가 \(\pi\)로 줄어듭니다.
- \(y=\sin 2\left(x-\frac{\pi}{6}\right)\)는 \(y=\sin 2x\)의 그래프를 \(x\)축의 양의 방향으로 \(\frac{\pi}{6}\)만큼 평행이동한 것입니다.
- \(y=\sin x + 3\)는 \(y=\sin x\)의 그래프를 \(y\)축의 양의 방향으로 \(3\)만큼 평행이동한 것입니다.
몇 가지 문제
최댓값과 최솟값
함수 \(y=a\cos(bx+c)+d\ (b\neq0)\)의 그래프의 주기와 최댓값, 최솟값은 다음과 같습니다.
- 주기 : \(\left|b\right| x=2\pi\)
- 최댓값 : \(\left|a\right|+d\)
- 최솟값 : \(-\left|a\right|+d\)
- 주의사항 : \(c\)값 자체가 평행이동은 아닙니다.
- 탄젠트 주기 : \(\left|b\right| x=\pi\)
주기 문제
보통 주기가 \(2\pi\)라고 주어지면, 이를 식으로 나타낼 때에는 \(f(x)=f(x+2\pi)\)로 표현을 합니다. 그렇지만, \(f(x)=f(x+2\pi)\)를 만족하는 함수는 \(y=\sin{x}\)도 해당되지만, \(y=\sin{2x}\)도 가능합니다. 원 식에 대입해서 좌우변이 같게 나오는 식들은 전부 해당이 됩니다. 주기를 보고 답을 찾아서는 안됩니다!!
절댓값과 주기
사인 함수와 코사인 함수는 \(y=\left|\sin{x}\right|\)는 주기가 절반으로 줄어듭니다. 그러나 탄젠트 함수는 그대로입니다.
또 한 가지 문제는 \(\displaystyle y=\left|5\cos\left(2x-\frac{\pi}{6}\right)+7\right|\)는 함숫값이 음의 값이 없으므로 절댓값이 없는 것과 마찬가지입니다.
\(y=\sin{\left|x\right|},\ y=\tan{\left|x\right|}\)는 주기함수가 아닙니다. 그러나 \(y=\cos{\left|x\right|}\)는 \(y\)축 대칭이므로 절댓값이 없는 것과 마찬가지가 되어 주기 함수입니다.
더해진 함수의 주기판정
보통 사인함수와 코사인함수가 더해져 있는 경우, 매개변수가 같으면 합성을 사용해서 주기를 구합니다.
그러나 매개변수가 서로 다를 경우에는 주기를 어떻게 구할까요?
이 경우에는 각각의 삼각함수에 대한 주기를 구한 후에 최소공배수가 주기가 됩니다. 예를 들어, \(y=\sin{2x}+\cos{3x}\)는 주기가 \(6\pi\)입니다.
평행이동
사인함수와 코사인함수는 최댓값과 최솟값에 이르는 영역의 범위가 같고 주기가 같다면 평행이동으로 겹칠 수 있는 그래프입니다.
응용예제
응용예제1
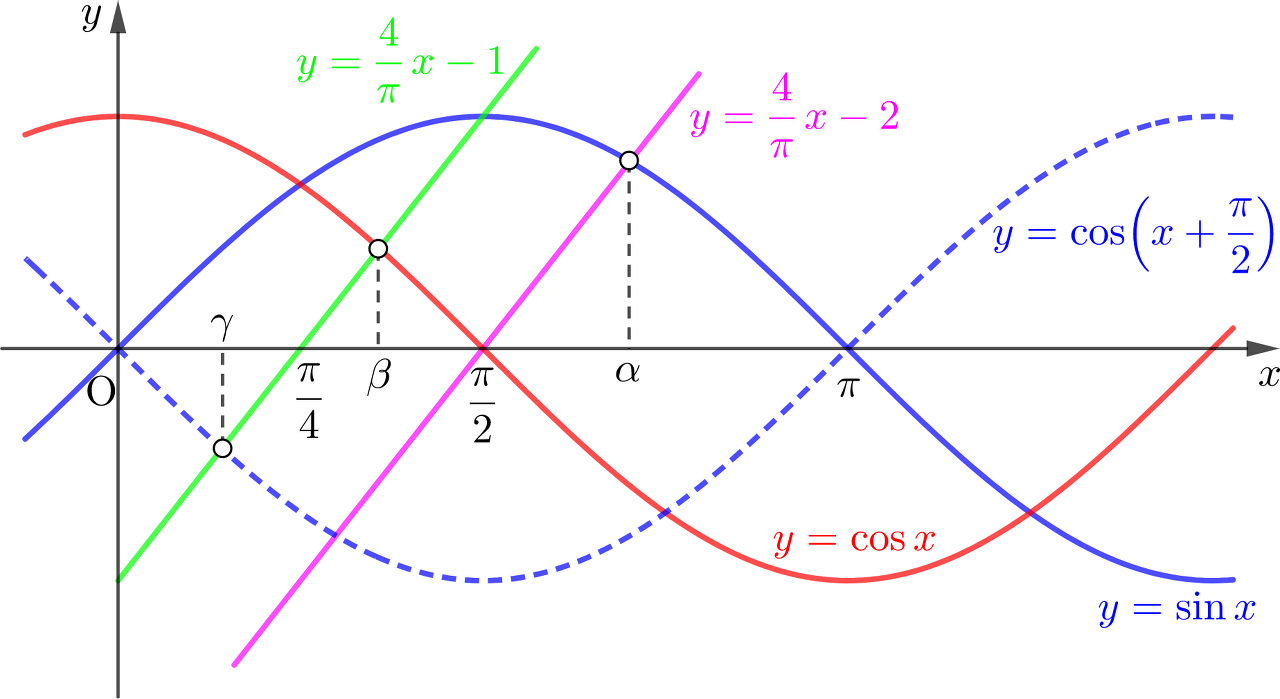
그림은 두 함수 \(y=\sin x\), \(y=\cos x\)의 그래프와 두 직선 \(\displaystyle y=\frac{4}{\pi}x-1\), \(y=\frac{4}{\pi}x-2\)을 나타낸 것입니다. 세 방정식
\(\quad\)\(\displaystyle \sin x = \frac{4}{\pi}x-2\)
\(\quad\)\(\displaystyle \cos x = \frac{4}{\pi}x-1\)
\(\quad\)\(\displaystyle \cos \left(x+\frac{\pi}{2}\right) = \frac{4}{\pi}x-1\)
의 실근을 각각 \(\alpha, \beta, \gamma\)라 할 때, 옳은 것을 다음에서 모두 고르세요.
\(\quad\)(가) \(\displaystyle \frac{\pi}{2} < \alpha < \frac{3}{4}\pi\)
\(\quad\)(나) \(\displaystyle \beta < \frac{2+\sqrt{2}}{8}\pi\)
\(\quad\)(다) \(\displaystyle \beta + \gamma = \frac{\pi}{2}\)