(번역) Irrational number

수학(mathematics)에서, 무리수(irrational numbers)는 유리수(rational number)가 아닌 모든 실수(real number)입니다. 즉, 무리수는 정수의 비율로 표현될 수 없습니다. 두 선분의 길이의 비율(ratio)이 무리수일 때, 선분은 역시 비-정수-비율-가능(incommensurable) 것으로 묘사되며, 그것들이 공통으로 "측정"을 공유할 수 없는, 즉, 얼마나 짧은지와 상관없이, 두 주어진 선분의 둘 다의 길이를 자체의 정수 배수로 표현하기 위해 사용될 수 있는 길이 ("측정")이 있지 않음을 의미합니다.
무리수 중에는 원의 지름에 대한 원의 둘레의 비율 π, 오일러의 숫자 e, 황금 비율 φ, 및 이의 제곱근(square root of two)이 있습니다; 사실, 완전 제곱수(perfect square)를 제외한 자연수(natural number)의 모든 제곱근은 무리수입니다.
모든 실수와 마찬가지로, 무리수는 위치적 표기법(positional notation), 특히 십진수로 표현될 수 있습니다. 무리수의 경우에 대해, 십진 전개는 종료하지 않거나, 반복하는 수열로 끝나지 않습니다. 예를 들어, π의 십진 표현은 3.14159로 시작하지만, 자릿수의 유한 개수는 정확하게 π를 나타낼 수도 없고, 그것이 반복되지도 않습니다. 반대로, 종료하거나 반복하는 십진 전개는 유리수여야 합니다. 이것들은 유리수와 위치적 숫자 시스템의 입증-가능한 속성이고, 수학에서 정의로 사용되지는 않습니다.
무리수는 역시 비-종료하는 연속된 분수(non-terminating continued fractions)와 많은 다른 방법으로 표현될 수 있습니다.
실수는 셀-수-없고 유리수(rationals)는 셀-수-있다는 칸토어의 증명(Cantor's proof)의 결과에 따르면, 거의 모든(almost all) 실수는 무리수입니다.

History

Ancient Greece

무리수의 존재의 첫 번째 증명은 보통 오각형(pentagram)의 변을 식별하는 동안 그것들을 발견했었던, 피타고라스-학파(Pythagorean) (아마도 메타폰툼의 히파주스(Hippasus of Metapontum))에 기인합니다. 당시의 피타고라스-학파 방법은 이들 길이 중 하나와 마찬가지로 다른 길이에 균등하게 맞출 수 있는 어떤 충분히 작고, 나눌 수 없는 단위가 있어야 한다고 주장했을 것입니다. 어쨌든, 히파주스는, 기원전 5세기에서, 실제로 공통 측정의 단위가 없었고, 그러한 존재의 주장은 사실상 모순이라고 추론할 수 있었습니다. 그는 이등변 직각 삼각형(isosceles right triangle)의 빗변(hypotenuse)이 실제로 다리를 갖는 정수-비율-가능(commensurable) 것이면, 그 측정의 단위에서 측정된 그것들의 길이 중 하나가, 불가능한 것인, 홀수와 짝수 둘 다여야 한다는 것을 시연함으로써 이것을 행했습니다. 그의 추론은 다음과 같습니다:

• 정수 a, b, 및 c의 변 길이를 갖는 이등변 직각 삼각형으로 시작합니다. 다리에 대한 빗변의 비율은 c:b로 표시됩니다.
• a, b, 및 c가 가장-작은 가능한 항에서 있다고 가정합니다 (즉, 그것들은 공통 인수를 가지지 않습니다).
• 피타고라스 정리(Pythagorean theorem)에 의해: \(c^2=a^2+b^2=b^2+b^2=2b^2\). (왜냐하면 삼각형이 이등변, a = b이기 때문입니다).
• \(c^2=2b^2\)이므로, \(c^2\)은 2로 나뉠 수 있고, 따라서 짝수입니다.
• \(c^2\)은 짝수이므로, c는 짝수여야 합니다.
• c가 짝수이며, c를 2로 나누는 것은 정수를 산출합니다. y를 이 정수로 놓습니다 (c = 2y).
• c = 2y의 양쪽 변을 제곱하는 것은 \(c^2=(2y)^2\), 또는 \(c^2=4y^2\)를 산출합니다.
• 첫 번째 방정식 \(c^2=2b^2\)에서 \(c^2\)에 대해 \(4y^2\)을 대체하는 것은 \(4y^2=2b^2\)을 제공합니다.
• 2로 나누는 것은 \(2y^2=b^2\)을 산출합니다.
• y는 정수이고, \(2y^2 = b^2\)이므로, \(b^2\)은 2로 나뉠 수 있고, 따라서 짝수입니다.
• \(b^2\)은 짝수이므로, b는 짝수여야 합니다.
• 우리는 단지 b와 c 둘 다가 짝수여야 한다는 것을 보여주었습니다. 따라서 그것들은 공통 인수로 2를 가집니다. 어쨌든 이것은 그것들이 공통 인수를 가지지 않는다는 가정과 모순됩니다. 이 모순은 c와 b가 둘 다 정수일 수 없고, 따라서 두 정수의 비율로 표현될 수 없는 숫자의 존재를 입증합니다.

그리스의 수학자들은 이러한 비-정수-비율-가능 규모의 이 비율을 alogos, 또는 말로 표현할 수 없다고 불렀습니다. 히파주스는, 어쨌든, 그의 노력에 대해 칭찬받지 못했습니다: 한 여담에 따르면, 그는 바다에 있는 동안 그의 발견을 만들었고, 그 후에 동료 피타고라스-학파 사람들에 의해 배 밖으로 던져졌습니다 "...우주에 있는 모든 현상이 정수와 그것들의 비율로 축소될 수 있다는 교리를...부인하는 원소를 우주에서 생성한 것 때문입니다." 또 다른 전설은 히파주스는 이 계시때문에 추방당했을 뿐이라고 전합니다. 히파주스 자신에게 어떤 결과가 있든, 그의 발견은 피타고라스-학파 수학에 매우 심각한 문제를 야기했는데, 왜냐하면 그것은 숫자와 기하학이 분리 불가능하다는 가정–그들 이론의 토대를 깨뜨렸기 때문입니다.
비-정수-비율-가능 비율의 발견은 그리스인에게 직면한 또 다른 문제: 이산과 연속의 관계를 암시하는 것입니다. 이것은 엘레아의 제논(Zeno of Elea)에 의해 밝혀졌으며, 그는 양이 이산이고 주어진 크기의 단위의 유한 숫자로 구성된다는 개념에 의문을 제기했습니다. 과거 그리스의 개념은 "정수는 구별되는 대상을 나타내고, 정수-비율-가능 비율은 구별되는 대상의 두 모음 사이의 관계를 나타냅니다"에 대해 반드시 그래야 한다고 규정했지만, 제논은 실제로 "[수량]은 일반적으로 단위의 이산 모음이 아닙니다; 이것이 바로 비-정수-비율-가능 [양]의 비율이 나타나는 이유입니다.... [수]량은, 달리 말해서, 연속적입니다"라는 것을 발견했습니다. 이것이 의미하는 바는 그 시대의 대중적인 개념과는 달리, 임의의 양에 대해 나눌-수-없고, 측정의 가장-작은 단위가 있을 수 없다는 것입니다. 사실, 이들 양의 나눗셈은 필연적으로 무한(infinite)해야 합니다. 예를 들어, 선분을 생각해 보십시오: 이 선분은 반으로 나뉠 수 있고, 그 반은 반으로 나뉠 수 있고, 그 반의 반은 반으로 나뉠 수 있고, 이런 식으로 계속됩니다. 이 과정은 무한히 계속될 수 있는데, 왜냐하면 항상 나뉠 수 있는 또 다른 반이 있기 때문입니다. 선분이 절반으로 줄어들수록, 측정의 단위는 영에 가까워지지만, 결코 정확히 영에 도달하지는 않습니다. 이것이 바로 제논이 입증하고자 한 것입니다. 그는 당시의 수학적 사고에 내재된 모순을 시연주는 네 가지 역설(four paradoxes)을 공식화함으로써 이것을 증명하고자 했습니다. 제논의 역설은 현재 수학적 개념의 결함을 정확하게 시연했지만, 그것들은 대안의 증명으로 여겨지지 않았습니다. 그리스인들의 생각에는, 한 관점의 타당성을 반증하는 것이 필연적으로 또 다른 관점의 타당성을 입증하는 것이 아니었고, 따라서 추가 조사가 필요했습니다.
다음 단계는 크니도스의 에우독소스(Eudoxus of Cnidus)에 의해 취해졌으며, 그는 정수-비율-가능 양과 마찬가지로 비-정수-비율-가능 양을 고려하는 새로운 비율의 이론을 공식화했습니다. 그의 아이디어의 중심은 크기와 숫자 사이의 구별이었습니다. 크기는 "...숫자가 아지만 선분, 각도, 넓이, 부피, 및 시간과 같은 엔터티를 나타내며, 이것들은 우리가 말했듯이 연속적으로 변할 수 있습니다. 크기는 4에서 5로 한 값에서 다른 값으로 점프하는 숫자와 반대되었습니다." 숫자는 어떤 가장 작고, 나뉠 수 없는 단위로 구성되지만, 크기는 무한하게 축소될 수 있습니다. 양적인 값이 크기에 할당되지 않았기 때문에, 에우독소스는 그-당시에 그것의 크기의 관점에서 비율과 두 비율 사이의 상등으로 비례를 정의함으로써 정수-비율-가능 비율과 비-정수-비율-가능 비율 둘 다를 설명할 수 있었습니다. 방정식 밖에서 양적인 값 (숫자)을 취함으로써, 그는 무리수를 숫자로 표현해야 하는 함정을 피했습니다. "에우독소스의 이론은 그리스 수학자들에게 비-정수-비율-가능 비율에 필요한 논리적 토대를 제공함으로써 기하학에서 엄청난 진전을 이룰 수 있게 했습니다." 이 비-정수-비율-가능성은 유클리드의 원론, 책 10, 제안 9에서 다루어집니다.
숫자와 크기 사이의 구별의 결과로써, 기하학은 비-정수-비율-가능 비율을 고려할 수 있는 유일한 방법이 되었습니다. 이전의 수치적 토대가 여전히 비-정수-비율-가능성의 개념과 양립할 수 없었기 때문에, 그리스인의 초점은 대수와 같은 수치적 개념에서 벗어나고 거의 전적으로 기하학에 초점을 맞추었습니다. 사실, 많은 경우에서 대수적 개념이 기하학적 용어로 다시-공식화되었습니다. 이것은 우리가 여전히 \(x^2\)과 \(x^2\)을 x의 두 번째 거듭제곱과 x의 세 번째 거듭제곱 대신에 x 제곱(squared) 및 x 세제곱(cubed)으로 표현하는 이유를 설명할 수 있습니다. 역시 비-정수-비율-가능 크기를 가진 제논의 연구에 결정적인 것은 초기 그리스 수학의 근본적인 균열로 인한 연역적 추론에 대한 근본적인 초점이었습니다. 기존 이론 이내의 일부 기본 개념이 현실과 상충된다는 깨달음은 해당 이론의 기초가 되는 공리와 가정의 완전하고 철저한 조사가 필요했습니다. 이 필요성에서, 에우독소스는 "...명시적인 공리에 기초하여 연역적 조직을 확립했습니다..." 마찬가지로 "...증명에 대해 연역적 추론에 의존하기로 한 초기 결정을 강화했습니다"라는 자신의 소진의 방법(method of exhaustion), 일종의 귀류법(reductio ad absurdum)을 개발했습니다. 이 소진의 방법은 미적분학의 생성에서 첫 번째 단계입니다.
씨이렌의 테오도루스(Theodorus of Cyrene)는 17까지의 정수의 제곱근(surds)의 무리성을 입증했지만, 아마도 거기에서 중단했는데 왜냐하면 그가 사용한 대수는 17의 제곱근에 적용할 수 없었기 때문입니다.
에우독소스(Eudoxus)가 유리적 비율과 마찬가지로 무리적 비율을 고려한 비례의 이론을 개발할 때까지 무리수의 강력한 수학적 기반은 생성되지 않았습니다.

India

제곱근과 같은 무리수를 포함하여 기하학적 및 수학적 문제는 인도에서 베다 시대(Vedic period) 동안 매우 일찍 다루어졌습니다. Samhita, Brahmana, 및 Shulba Sutras (기원전 800년 또는 이전)에 그러한 계산에 대한 참조가 있습니다. (Bag, Indian Journal of History of Science, 25(1-4), 1990를 참조하십시오).
기원전 7 세기 이후, 마나바(Manava) (기원전 c. 750 – 690)는 2와 61과 같은 숫자의 제곱근(square root)은 정확히 결정할 수 없다고 믿었을 때, 무리성의 개념은 인도의 수학자들(Indian mathematicians)에 의해 암묵적으로 받아들여졌다고 제안되었습니다. 어쨌든, 역사가 칼 벤자민 보이어(Carl Benjamin Boyer)는 "그러한 주장은 입증되지 않았고 사실일 가능성이 낮다"라고 썼습니다.
역시 아리아바타(Aryabhata) (기원후 5세기)는, π의 값을 다섯 유효 숫자로 계산하는 것에서, 이것이 근사일 뿐만 아니라 그 값이 비-정수-비율-가능 (또는 무리적)임을 의미하기 위해, 단어 āsanna (접근)를 사용했습니다.
나중에, 그들의 논문에서, 인도의 수학자들은 덧셈, 뺄셈, 곱셈, 유리화, 마찬가지로 제곱근의 분리와 추출을 포함한 제곱근의 산술에 대해 썼습니다.
브라마굽타(Brahmagupta) (기원후 628년)와 바스카라 1세(Bhāskara I) (기원후 629년)와 같은 수학자들은 다른 수학자들이 그랬던 것처럼 이 분야에 공헌했습니다. 12세기에서, 바스카라 2세(Bhāskara II)는 이들 공식 중 일부를 평가하고 그것을 분석적으로 평가하여, 그것들의 한계를 확인했습니다.
14에서 16세기 동안 산가마그라마의 마드하바(Madhava of Sangamagrama)와 천문학과 수학의 케랄라 학교(Kerala school of astronomy and mathematics)는 π 및 삼각 함수(trigonometric functions)의 특정 무리 값과 같은 여러 무리수에 대해 무한 급수(infinite series)를 발견했습니다. 지드데바(Jyesthadeva)는 Yuktibhāṣā에서 이들 무한 급수에 대해 증명을 제공했습니다.

Middle Ages

중세(Middle ages)에서, 무슬림 수학자들(Muslim mathematicians)에 의한 대수학(algebra)의 발달은 무리수를 대수적 대상(algebraic objects)으로 취급되는 것을 허용했습니다. 중동의 수학자들은 역시 "숫자(number)"와 "크기(magnitude)"의 개념을 보다 일반적인 실수(real number)의 아이디어로 병합하고, 유클리드의 비율(ratio)의 아이디어를 비판하고, 복합 비율의 이론을 발전시켰고, 연속 크기의 비율에 대한 숫자의 개념을 확장했습니다. 원론의 책 10에 대한 그의 주석에서, 페르시아(Persian) 수학자 알-마하니(Al-Mahani) (d. 874/884)는 이차 무리수(quadratic irrational)와 삼차 무리수를 조사하고 분류했습니다. 그는 유리수와 무리수 크기에 대해 정의를 제공했으며, 그는 이것을 무리수로 취급했습니다. 그는 그것들을 자유롭게 다루었지만 기하학적 용어로 다음과 같이 설명합니다:

"우리가, 예를 들어, 10, 12, 3%, 6%, 등을 말하면 그 값이 유리수 (크기)일 것인데, 왜냐하면, 그것의 값은 양적으로 발음되고 표현되기 때문입니다. 유리수가 아닌 무엇은 무리수이고 그것은 발음하고 양적으로 그 값을 나타내는 것이 불가능합니다. 예를 들어: 제곱가 아닌 10, 15, 20과 같은 숫자의 근, 세제제곱이 아닌 숫자의 변 등."

직선으로 유클리드의 크기의 개념과는 달리, 알-마하니는 정수와 분수를 유리적 크기로, 제곱근과 세제곱근(cube root)을 무리적 크기로 여겼습니다. 그는 역시 무리성의 개념에 대한 산술(arithmetic)적 접근을 도입했는데, 왜냐하면 그는 다음을 무리수 크기로 여겼기 때문입니다:

"그들의 합 또는 차이, 또는 유리수 크기에 덧셈한 결과, 또는 무리수 크기에서 이 종류의 크기를 뺀 결과, 또는 그것에서 유리수 크기를 뺀 결과."

이집트(Egypt)의 수학자 아부 카밀 쇼하 이븐 아슬람(Abū Kāmil Shujā ibn Aslam) (c. 850 – 930)은 처음으로 무리수를 이차 방정식(quadratic equation)의 해로 또는 방정식(equation)에서, 종종 제곱 근, 세제곱 근 및 네제곱 근(fourth roots)의 형식에서 계수(coefficient)로 받아들였습니다. 10세기에서, 이라크(Iraq)의 수학자 알-헤시미(Al-Hashimi)는 곱셈, 나눗셈 및 기타 산술 함수를 고려할 때 무리수에 대해 (기하학적 시연이 아닌) 일반적인 증명을 제공했습니다. 이란의 수학자, 아부 자파르 알-카진(Abū Ja'far al-Khāzin) (900–971)은 무리수와 유리수 크기의 정의를 제공했으며, 한정된 양(quantity)이 다음과 같으면, 다음을 말합니다:

"특정 주어진 크기 한 번 또는 여러 번 포함되면, 이 (주어진) 크기는 유리수에 해당합니다. . . . 이 (후자의) 크기가 (단위의) 주어진 크기의 1/2, 1/3, 또는 1/4을 구성할 때마다, 또는, (단위)와 비교된, 3, 5, 또는 3/5로 구성할 때마다, 그것은 유리수 크기입니다. 그리고, 일반적으로, 이 크기 (즉, 단위)에 해당하는 각 크기는, 하나의 숫자에서 또 다른 숫자로, 유리수입니다. 만약, 어쨌든, 크기는 주어진 크기의 배수, 부분 (1/n) 또는 부분들 (m/n)로 표현될 수 없으면, 그것은 무리수이며, 즉, 그것은 근에 의한 것 외에 표현될 수 없습니다."

이들 개념의 대부분은 12세기의 라틴어 번역 후 어떤 때에 유럽의 수학자들에 의해 결국 받아들여졌습니다. 알-하사르(Al-Hassār), 12세기 동안 이슬람 상속 법리학을 전공한 Fez 출신의 모로코 수학자는 분수적 막대의 사용을 처음 언급했으며, 여기서 분자(numerator)와 분모는 수평 막대로 구분됩니다. 그의 논의에서, 그는 썼습니다, "..., 예를 들어, 만약 여러분이 3/5과 1/3을 작성하라는 지시를 받았다면, 이렇게 쓰십시오, \(\frac{3 \quad 1}{5 \quad 3}\)." 이와 같은 분수적 표기법은 13세기에서 레오나르도 피보나치(Leonardo Fibonacci)의 연구에서 곧 나타납니다.

Modern period

17세기에서, 허수(imaginary number)는 아브라암 드 무아브르(Abraham de Moivre), 및 특히 레온하르트 오일러(Leonhard Euler)의 손에서 강력한 도구가 되었습니다. 19세기에서 복소수(complex number) 이론의 완성은 무리수의 차별을 대수적 및 초월적 숫자(transcendental numbers)로, 초월적 숫자의 존재의 증명, 및 무리수의 이론의 과학적 연구의 부활을 수반했으며, 유클리드(Euclid) 이후 크게 무시되었던 것입니다. 1872년에서, 카를 바이어슈트라스(Karl Weierstrass) (그의 학생 에른스트 코삭(Ernst Kossak)), 에두아르트 하이네(Eduard Heine) (Crelle's Journal, 74), 게오르크 칸토어(Georg Cantor) (Annalen, 5), 및 리하르트 데데킨트(Richard Dedekind)의 이론이 출판되었습니다. 머라이(Méray)는 1869년에 하이네(Heine)와 같은 출발점을 취했지만, 이론은 일반적으로 1872년으로 참조됩니다. 바이어슈트라스(Weierstrass)의 방법은 1880년에 살바토르 핀케를레(Salvatore Pincherle)에 의해 완전히 설명되었고, 데데킨트(Dedekind)의 것은 저자의 나중 연구 (1888)와 폴 태너리(Paul Tannery) (1894)에 의한 승인을 통해 추가로 주목을 받았습니다. 바이어슈트라스(Weierstrass), 칸토어(Cantor) 및 하이네(Heine)는 무한 급수에 대한 그들의 이론을 기반으로 하지만, 데데킨트(Dedekind)는 실수(real number)의 시스템에서 자름 (cut, Schnitt)의 아이디어를 발견했으며, 모든 유리수(rational number)를 어떤 특성 속성을 갖는 두 그룹으로 분리합니다. 그 주제는 나중에 바이어슈트라스, 레오폴트 크로네커(Leopold Kronecker) (Crelle, 101), 및 샬롯 미레이(Charles Méray)의 손에서 기고를 받았습니다.
연속된 분수(Continued fraction)는, 무리수에 밀접하게 관련되고 (1613년 카탈디에 기인하며), 오일러의 손에 주목을 받았고, 19세기 초에서 조제프-루이 라그랑주(Joseph-Louis Lagrange)의 저술을 통해 눈에 띄게 되었습니다. 디리클레(Dirichlet)는 역시 주제의 적용에 많은 기여자들이 있기 때문에 일반 이론에 더했습니다.
요한 하인리히 램버트(Johann Heinrich Lambert)는 π가 유리수일 수 없고 \(e^n\)은 만약 n이 유리수이면 (n = 0이 아니면) 무리수라는 것을 증명했습니다 (1761). 램버트의 증명은 종종 불완전하다고 불리지만, 현대적인 평가는 그것을 만족스러운 것으로 지원하고, 실제로 그 당시에 그것은 비정상적으로 엄격합니다. 아드리앵-마리 르장드르(Adrien-Marie Legendre) (1794)는, 베셀-클리퍼드 함수(Bessel-Clifford function)를 도입한 후, \(\pi^2\)이 무리수이며, 바로 뒤따라 π도 역시 무리수라는 것을 보이기 위해 증명을 제공했습니다. 초월적 숫자(transcendental number)의 존재는 리우빌(Liouville) (1844, 1851)에 의해 처음 확립되었습니다. 나중에, 게오르크 칸토어(Georg Cantor) (1873)는 다른 방법에 의한 그것들의 존재를 입증했으며, 이것은 현실에서 모든 각 구간이 초월적 숫자를 포함함을 보였습니다. 샤를 에르미트(Charles Hermite) (1873)는 처음으로 e가 초월적임을 입증했고, 페르디난트 폰 린데만(Ferdinand von Lindemann) (1882)는, 에르미트의 결론에서 시작하여, π에 대해 같은 것임을 보었습니다. 린데만의 증명은 바이어슈트라스 (1885)에 의해, 더 나아가 다비트 힐베르트(David Hilbert) (1893)에 의해 훨씬 단순화되었고, 마침내 아돌프 후르비츠(Adolf Hurwitz)와 파울 고르단(Paul Gordan)에 의해 기본이 되었습니다.

Examples

Square roots

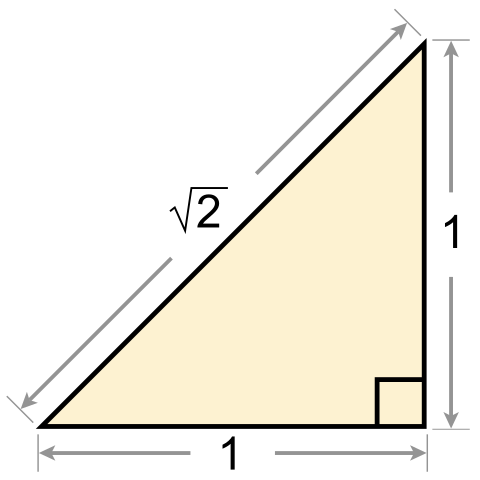
2의 제곱근(square root of 2)은 무리수로 입증된 최초의 숫자였고, 해당 기사는 여러 증명을 포함합니다. 황금 비율(golden ratio)은 또 다른 유명한 이차 무리수입니다. 완전 제곱(perfect squares)이 아닌 모든 자연수의 제곱근은 무리수이고 증명은 이차 무리수(quadratic irrational)에서 찾아질 수 있습니다.

General roots

이의 제곱근에 대해 위의 증명은 산술의 기본 정리(fundamental theorem of arithmetic)를 사용하여 일반화될 수 있습니다. 이것은 모든 각 정수가 소수로의 고유한 인수분해(unique factorization)를 가진다고 주장합니다. 그것을 사용하여 우리는 만약 유리수가 정수가 아니면 그것의 정수 거듭제곱이 정수가 될 수 없으며, 가장-낮은 항(lowest terms)에서 처럼 분모에서 거듭제곱 각각이 어떤 것이 올려져 있는지에 관계없이 분자로 나누지 않는 소수(prime)가 있어야 함을 보여줄 수 있습니다. 그러므로, 만약 정수가 또 다른 정수의 정확히 k번째 거듭제곱이 아니면, 해당 첫 번째 정수의 k번째 근(kth root)은 무리수입니다.

Logarithms

아마도 무리수임을 입증하기 가장 쉬운 숫자는 특정 로그(logarithm)일 것입니다. 여기에 log2 3이 무리수라는 모순에 의한 증명(proof by contradiction)이 있습니다 (\(\log_2 3\) ≈ 1.58 > 0).
\(\log_2 3\)이 유리수임을 가정합니다. 어떤 양의 정수 m과 n에 대해, 우리는 다음을 가집니다:
\(\quad\)\(\displaystyle \log_2 3 = \frac{m}{n}.\)
그것은 다음임을 따릅니다:
\(\quad\)\(2^{m/n}=3\)
\(\quad\)\((2^{m/n})^n = 3^n\)
\(\quad\)\(2^m=3^n.\)
어쨌든, 임의의 양의 정수 거듭제곱이 올려진 숫자 2는 짝수여야 하고 (왜냐하면 그것은 2로 나누어집니다) 임의의 양의 정수 거듭제곱이 올려진 숫자 3은 홀수여야 합니다 (왜냐하면 그것의 소수 인수(prime factor) 어떤 것도 2가 아닐 것입니다). 분명히 정수는 동시에 홀수와 짝수 둘 다일 수 없습니다: 우리는 모순에 빠집니다. 우리가 만든 유일한 가정은 \(\log_{2} 3\)이 유리수 (및 따라서 n ≠ 0을 갖는 정수의 몫 m/n으로 표현할 수 있음)라는 것입니다. 모순은 이 가정이 거짓, 즉, \(\log_{2} 3\)은 무리수이고, n ≠ 0을 갖는 정수의 몫 m/n으로 결코 표현될 수 없음을 의미합니다.
\(\log_{10} 2\)와 같은 경우도 유사하게 처리될 수 있습니다.

Types

• 숫자 이론적 구별 : 초월적/대수적
• 정규(normal)/ 이상(abnormal, 비-정규)

Transcendental/algebraic

거의 모든(Almost all) 무리수는 초월적(transcendental)이고 모든 실수 초월적 숫자는 무리수입니다 (역시 복소 초월적 숫자가 있습니다): 초월적 숫자에 대한 기사는 여러 예제를 목록화합니다. 따라서 \(e^r\)과 \(\pi^r\)은 모든 비-영 유리수 r에 대해 무리수이고, 예를 들어, \(e^{\pi}\)도 무리수입니다.
무리수는 역시 실수 대수적 숫자(algebraic number)의 셀-수-있는(countable) 집합 (본질적으로 정수 계수를 갖는 다항식(polynomial)의 실수 근(roots)으로 정의됨), 즉 다음 다항 방정식의 실수 해 내에서 찾아질 수 있습니다:
무리수는 역시 실수 대수적 숫자(algebraic number)의 셀-수-있는(countable) 집합 (본질적으로 정수 계수를 갖는 다항식(polynomial)의 실수 근(roots)으로 정의됨), 즉 다음 다항 방정식의 실수 해 내에서 찾아질 수 있습니다:
\(\quad\)\(p(x) = a_nx^n + a_{n-1}x^{n-1} + \cdots + a_1x + a_0 = 0\;, \)
여기서 계수 \(a_i\)는 정수이고 \(a_n \ne 0\)입니다. 이 다항 방정식의 임의의 유리 근(any rational root)은 형식 r/s의 것이어야 하며, 여기서 r은 \(a_0\)의 약수(divisor)이고 s는 \(a_n\)의 약수입니다. 만약 다항식 \(p\)의 실수 근 \(x_0\)가 이들 유한하게 많은 가능성에 속하지 않으면, 그것은 무리 대수적 숫자여야 합니다. 그러한 대수적 무리수의 존재에 대해 예시적인 증명은 \(x_0=(2^{1/2}+1)^{1/3}\)이 정수 계수를 갖는 다항식의 무리 근임을 보이는 것입니다: 그것은 \((x^3-1)^2=2\)를 만족시키고 따라서 \(x^6-2x^3-1=0\)이고, 이 후자의 다항식은 유리 근을 가지지 않습니다 (확인할 유일한 후보는 ±1이고, 1보다 더 큰 \(x_0\)는 이 둘 중 어느 것도 아닙니다), 따라서 \(x_0\)은 무리 대수적 숫자입니다.
대수적 숫자는 실수의 부분필드(subfield)를 형성하기 때문에, 많은 무리적 실수는 초월적 및 대수적 숫자를 결합함으로써 구성될 수 있습니다. 예를 들어, \(3\pi + 2\), \(3\pi + 2\), \(\pi+\sqrt{2}\), 및 \(e\sqrt{3}\)은 무리수입니다 (그리고 심지어 초월적입니다).

Decimal expansions

무리수의 십진 전개는 임의의 유리수와 달리 반복되거나 끝나지 않습니다 (종료는 반복되는 0과 동등합니다). 같은 것은 이진(binary), 팔진(octal) 또는 십육진(hexadecimal) 전개에 대해 참이고, 일반적으로 자연수(natural) 기저를 갖는 모든 각 위치적(positional) 표기법(notation)에 대해 참입니다.
이것을 보여주기 위해, 우리는 정수 n을 m으로 나눈다고 가정합니다 (여기서 m은 비-영입니다). 긴 나눗셈(long division)이 m에 의한 n의 나눗셈에 적용될 때, 오직 m 나머지가 가능합니다. 만약 0이 나머지로 나타나면, 십진 전개는 종료됩니다. 만약 0이 결코 발생하지 않으면, 알고리듬은 임의의 나머지를 두 번 이상 사용 없이 많아야 m − 1 단계를 실행할 수 있습니다. 그 후에, 나머지가 반복되어야 하고, 그런-다음 십진 전개가 반복됩니다.
반대로, 우리가 반복되는 십진(repeating decimal)에 직면했다고 가정하면, 우리는 그것이 두 정수의 분수임을 증명할 수 있습니다. 예를 들어, 다음을 생각해 보십시오:
\(\quad\)\(A=0.7\,162\,162\,162\,\ldots\)
여기서 반복마디는 162이고 반복마디의 길이는 3입니다. 먼저, 우리는 먼저 십진점이 반복마디의 바로 앞에 오도록 그것을 오른쪽으로 이동하기 위해 적절한 10의 거듭제곱을 곱합니다. 이 예에서, 우리는 그것을 얻기 위해 10을 곱할 것입니다:
\(\quad\)\(10A = 7.162\,162\,162\,\ldots\)
이제 우리는 이 방정식에 \(10^r\)을 곱하는데 여기서 r은 반복마디의 길이입니다. 이것은 "다음" 반복마디 앞에 십진점을 이동하는 효과를 가집니다. 우리의 예제에서, \(10^3\)을 곱합니다:
\(\quad\)\(10,000A=7\,162.162\,162\,\ldots\)
두 곱셈의 결과는 정확히 같은 "십진 일부"를 갖는 두 다른 표현을 제공합니다. 즉, 10,000A의 꼬리 끝은 정확히 10A의 꼬리 끝과 일치합니다. 여기서 10,000A와 10A 둘 다는 십진 점 후에 .162162162...를 가집니다.
그러므로, 우리가 10,000A 방정식에서 10A 방정식을 뺄 때, 10A의 꼬리 끝은 10,000A의 꼬리 끝을 삭제하고 다음을 남깁니다:
\(\quad\)\(9990A=7155.\)
그런-다음 다음은
\(\quad\)\(\displaystyle A= \frac{7155}{9990}\)
정수의 비율이고 따라서 유리수입니다.

Irrational powers

다브 자든(Dov Jarden)은 ab가 유리수를 만족하는 두 무리수 a와 b가 존재한다는 간단한 비-구성적 증명(constructive proof)을 제공했습니다:
\(\sqrt{2}^{\sqrt{2}}\)를 생각해 보십시오; 만약 이것이 유리수이면, \(a=b=\sqrt{2}\)를 취합니다. 그렇지 않으면, a를 무리수 \(\sqrt{2}^{\sqrt{2}}\)가 되도록 취하고 \(b=\sqrt{2}\)를 취합니다. 그런-다음 \(a^b=\left(\sqrt{2}^{\sqrt{2}}\right)^{\sqrt{2}}=\sqrt{2}^{\sqrt{2}\cdot \sqrt{2}}=\sqrt{2}^2=2\), 이것은 유리수입니다.
비록 위의 논증이 두 경우 사이를 결정하지는 않을지라도, 겔폰트–슈나이더 정리(Gelfond–Schneider theorem)는 \(\sqrt{2}^{\sqrt{2}}\)가 초월적(transcendental)이므로, 무리수라는 것을 보여줍니다. 이 정리는 만약 a와 b가 둘 다 대수적 숫자(algebraic number)이고, a가 0 또는 1과 같지 않고, b가 유리수가 아니면, \(a^b\)의 임의의 값은 초월적 숫자임을 보여줍니다 (만약 복소수 지수(complex number exponentiation)가 사용되면 하나의 값보다 많은 것이 있을 수 있습니다).
간단한 구성적 증명을 제공하는 예제는 다음입니다:
\(\quad\)\(\displaystyle \left(\sqrt{2}\right)^{\log_{\sqrt{2}}3}=3.\)
왼쪽 변의 밑수가 무리수이고 오른쪽 변은 유리수이므로, 우리는 왼쪽 변에서 지수, \(\log_{\sqrt{2}}3\)이 무리수임을 입증해야 합니다. 이것은 그런데 왜냐하면, 다른 밑수를 갖는 로그와 관련된 다음 공식에 의해 그렇습니다:
\(\quad\)\(\displaystyle \log_{\sqrt{2}}3=\frac{\log_2 3}{\log_2 \sqrt{2}}=\frac{\log_2 3}{1/2} = 2\log_2 3\)
이것은 우리가, 모순(contradiction)을 확립하기 위해, 양의 정수의 m/n 비율과 같다고 가정할 수 있습니다. 그런-다음 \(\log_2 3 = m/2n\)이므로 \(2^{\log_2 3}=2^{m/2n}\)이므로 \(3=2^{m/2n}\)이므로 \(3^{2n}=2^m\)이며, 이것은 모순적인 소수 인수분해의 쌍이고 따라서 산술의 기본 정리(fundamental theorem of arithmetic) (고유한 소수 인수분해)를 위반합니다.
더 강한 결과는 다음과 같습니다: 구간 \(((1/e)^{1/e}, \infty)\)에서 모든 각 유리수는 어떤 무리수 a에 대해 \(a^a\)로 또는 어떤 자연수 n에 대해 \(n^n\)으로 쓰일 수 있습니다. 유사하게, 모든 각 양의 유리수는 어떤 무리수 a에 대해 \(\displaystyle a^{a^a}\)로 또는 어떤 자연수 n에 대해 \(\displaystyle n^{n^n}\)으로 쓰일 수 있습니다.

Open questions

\(\pi+e\) (또는 \(\pi-e\))가 무리수인지 여부는 알려지지 않았습니다. 사실, \(m\pi+ n e\)가 무리수인지 여부를 알려주는 비-영 정수 쌍 \(m, n\)이 없습니다. 게다가, 집합 \(\{\pi, e\}\)이 \(\mathbb{Q}\)에 걸쳐 대수적으로 독립(algebraically independent)인지 여부는 알려지지 않았습니다.
\(\pi e,\ \pi/e,\ 2^e,\ \pi^e,\ \pi^\sqrt{2},\ \ln\pi,\) 카탈란의 상수(Catalan's constant), 또는 오일러–마스케로니 상수(Euler–Mascheroni constant) \(\gamma\)가 무리수인지 여부는 알려지지 않았습니다. 테트레이션(tetration)  \(^n\pi\) 또는 \(^n e\)의 하나가 어떤 정수 \(n > 1\)에 대해 유리수인지 여부는 알려지지 않았습니다.

Set of all irrationals

실수는 셀-수-없는(uncountable) 집합을 형성하고, 유리수는 그것의 셀-수-있는(countable) 부분집합이므로, 무리수의 여적인 집합은 셀-수-없는 것입니다.
보통 (유클리드(Euclidean)) 거리 함수 d(x, y) = |x − y| 아래에서, 실수는 메트릭 공간(metric space)이고 따라서 역시 토폴로지적 공간(topological space)입니다. 유클리드 거리 함수를 제한하는 것은 메트릭 공간의 무리수 구조를 제공합니다. 무리수의 부분공간은 닫혀있지 않기 때문에, 유도된 메트릭은 완비(complete)가 아닙니다. 어쨌든, 완비 메트릭 공간에서 G-델타 집합(G-delta set)–즉, 열린 부분집합의 셀-수-있는 교집합–이 있는 것, 무리수의 공간은 완전하게 메트릭-가능(completely metrizable)입니다: 즉, 유클리드 메트릭의 제한과 같은 토폴로지를 유도하는 무리수에 대한 메트릭이 있지만, 그것에 관해 무리수는 완비입니다. 우리는 G-델타 집합에 대한 앞서 언급한 사실을 몰라도 이것을 알 수 있습니다: 무리수의 연속된 분수(continued fraction) 전개는 무리수의 공간에서 양의 정수의 모든 수열의 공간으로의 위상-동형을 정의하며, 이것은 완전하게 메트릭-가능임을 쉽게 보일 수 있습니다.
게다가, 모든 무리수의 집합은 비-연결된 메트릭-가능 공간입니다. 사실, 부분공간 토폴로지를 구비된 무리수는 닫힌-열린 집합(clopen set)의 기반을 가지고 있으므로 공간은 영-차원입니다.

Further reading

• Adrien-Marie Legendre, Éléments de Géometrie, Note IV, (1802), Paris
• Rolf Wallisser, "On Lambert's proof of the irrationality of π", in Algebraic Number Theory and Diophantine Analysis, Franz Halter-Koch and Robert F. Tichy, (2000), Walter de Gruyer

External links

 

• Zeno's Paradoxes and Incommensurability (n.d.). Retrieved April 1, 2008
• Weisstein, Eric W. "Irrational Number". MathWorld.