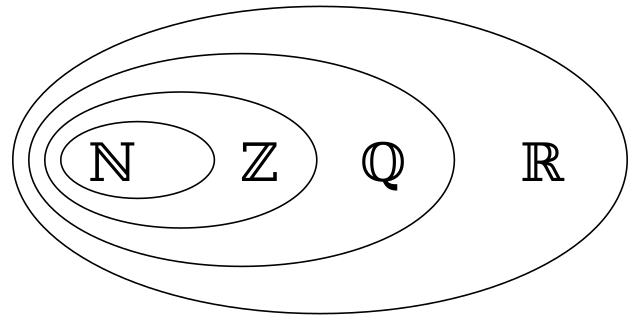
수학(mathematics)에서, 유리수(rational number)는 두 정수(integer), 분자(numerator) p와 비-영 분모(denominator) q의 몫(quotient) 또는 분수(fraction) p/q로 표현될 수 있는 −3/7와 같은 숫자(number)입니다. 모든 각 정수는 유리수입니다: 예를 들어, 5 = 5/1. "유리(the rationals)", 유리의 필드(field of rationals) 또는 유리수의 필드(field of rational numbers)로 종종 참조되는, 모든 유리수의 집합(set)은 보통 굵은-글씨 Q (또는 칠판 굵은-글씨(blackboard bold) \(\mathbb{Q}\), 𝐐/ℚ)로 표시됩니다; 그것은 따라서 1895년에 주세페 페아노(Giuseppe Peano)에 의한 "quotient"에 대해 이탈리아어 quoziente 이후에 표시되었습니다.
유리수의 십진 전개(decimal expansion)는 자릿수(digits)의 유한 숫자 후에 종료하는 것 (예를 들어: 3/4 = 0.75), 또는 결국 같은 유한 자릿수의 수열(sequence)을 계속 반복(repeat)하기 시작하는 것 (예를 들어: 9/44 = 0.20454545...) 중 하나입니다. 반대로, 임의의 반복하는 또는 종료하는 십진수는 유리수를 나타냅니다. 이들 명제는 밑수 10(base 10)에서 뿐만 아니라, 임의의 다른 정수 밑수(base) (예를 들어, 이진수(binary) 또는 십육진수(hexadecimal))에서도 참입니다.
유리수가 아닌 실수(real number)는 무리수(irrational)라고 불립니다. 무리수는 \(\sqrt{2}\), π, e, 및 φ를 포함합니다. 무리수의 십진 전개(decimal expansion)는 반복 없이 계속됩니다. 유리수의 집합은 셀-수-있고(countable), 실수의 집합은 셀-수-없기(uncountable) 때문에, 거의 모든(almost all) 실수는 무리수입니다.
유리수는, 다음처럼 정의된 동치 관계(equivalence relation)를 사용하여, q ≠ 0을 갖는 정수 쌍 (p, q)의 동치 클래스(equivalence class)로 공식적으로(formally) 정의될 수 있습니다:
\(\quad\)\(\left( p_1, q_1 \right) \sim \left( p_2, q_2 \right) \iff p_1 q_2 = p_2 q_1.\)
분수 p/q는 그런-다음 (p, q)의 동치 클래스를 표시합니다.
덧셈(addition) 및 곱셈(multiplication)과 함께 유리수는 정수(integer)를 포함하는 필드(field)를 형성하고, 정수를 포함하는 임의의 필드에 포함됩니다. 달리 말해서, 유리수의 필드는 소수 필드(prime field)이고, 필드가 특성 영(characteristic zero)을 가지는 것과 그것이 유리수를 부분필드로 포함하는 것은 필요충분 조건입니다. Q의 유한 확장(extensions)은 대수적 숫자 필드(algebraic number field)라고 불리우고, Q의 대수적 클로저(algebraic closure)는 대수적 숫자(algebraic number)의 필드입니다.
수학적 해석학(mathematical analysis)에서, 유리수는 실수의 조밀한 부분집합(dense subset)을 형성합니다. 실수는 코시 수열(Cauchy sequence), 데데킨트 자름(Dedekind cut), 또는 무한 십진(decimal)을 사용하여, 완비에 의해 유리수로부터 구성될 수 있습니다 (자세한 것에 대해, 실수의 구성(Construction of the real numbers)을 참조하십시오).
Terminology
집합 Q에 대한 참조에서 용어 유리(rational)는 유리수가 두 정수의 비율(ratio)을 나타내는 사실을 참조합니다. 수학에서 "rational"는 종종 "유리수"를 약칭하는 명사로 사용됩니다. 형용사 rational은 때때로 계수(coefficient)가 유리수임을 의미합니다. 예를 들어, 유리 점(rational point)은 유리 좌표(coordinates)를 갖는 점 (즉, 그것의 좌표가 유리수인 점)입니다; 유리 행렬은 유리수의 행렬(matrix)입니다; 유리 다항식은 비록 "유리에 걸쳐 다항식"이 일반적으로 선호될지라도, "유리 표현(rational expression)" 및 "유리 함수(rational function)" (다항식이 유리 표현이고, 심지어 그것의 계수가 유리수가 아닐지라도, 유리 함수를 정의합니다) 사이의 혼동을 피하기 위해 유리 계수를 가진 다항식일 수 있습니다. 어쨌든, 유리 곡선(rational curve)은 유리에 걸쳐 정의된 곡선이 아니지만, 유리 함수에 의해 매개변수화될 수 있는 곡선입니다.
Arithmetic
Irreducible fraction
모든 각 유리수는 고유한 방법에서 기약 분수(irreducible fraction) a/b를 표현할 수 있으며, 여기서 a와 b는 서로소 정수(coprime integers)이고 b > 0입니다. 이것은 종종 유리수의 정식의 형식(canonical form)이라고 불립니다.
유리수 a/b로 시작하여, 그것의 정식의 형식은 a와 b를 그것들의 최대 공통 약수(greatest common divisor)로 나눔으로써 얻어질 수 있고, 만약 b < 0이면, 결과 분자와 분모의 부호를 변경합니다.
Embedding of integers
임의의 정수 n은 유리수 n/1로 표현될 수 있으며, 이것은 유리수로 그것의 정식의 형식입니다.
Equality
\(\quad\)\(\displaystyle \frac{a}{b} = \frac{c}{d}\)인 것과 \(ad = bc\)인 것은 필요충분 조건입니다.
만약 두 분수가 정식의 형식에 있으면, 다음입니다:
\(\quad\)\(\displaystyle \frac{a}{b} = \frac{c}{d}\)인 것과 \(a = c\)와 \(b = d\)인 것은 필요충분 조건입니다.
Ordering
만약 두 분모가 양수이면 (특히 두 분수가 정식의 형식에 있으면):
\(\quad\)\(\displaystyle \frac{a}{b} < \frac{c}{d}\)인 것과 \(ad < bc.\)인 것은 필요충분 조건입니다.
다른 한편으로, 만약 두 분모가 음수이면, 음의 분모를 갖는 각 분수는 먼저 그것의 분자와 분모 둘 다의 부호를 변경함으로써 양의 분모를 갖는 동등한 형식으로 반드시 변경되어야 합니다.
Addition
두 분수는 다음처럼 더해집니다:
\(\quad\)\(\displaystyle \frac{a}{b} + \frac{c}{d} = \frac{ad+bc}{bd}.\)
만약 두 분수가 정식의 형식에 있으면, 그 결과가 정식의 형식에 있는 것과 b와 d가 서로소 정수(coprime integers)인 것은 필요충분 조건입니다.
Subtraction
\(\quad\)\(\displaystyle \frac{a}{b} - \frac{c}{d} = \frac{ad-bc}{bd}.\)
만약 두 분수가 정식의 형식에 있으면, 그 결과가 정식의 형식에 있는 것과 b와 d가 서로소 정수(coprime integers)인 것은 필요충분 조건입니다.
Multiplication
곱셈에 대해 규칙은 다음입니다:
\(\quad\)\(\displaystyle \frac{a}{b} \cdot\frac{c}{d} = \frac{ac}{bd}.\)
여기서 그 결과는 심지어 두 원래 분수가 정식의 형식에 있을지라도 비-기약 분수(reducible fraction)일 수 있습니다.
Inverse
모든 각 유리수 a/b는 덧셈의 역(additive inverse)을 가지며, 종종 그것의 반대(opposite)라고 불립니다:
\(\quad\)\(\displaystyle - \left( \frac{a}{b} \right) = \frac{-a}{b}.\)
만약 a/b가 정식의 형식에 있으면, 같은 것은 그것의 반대에 대해 참입니다.
비-영 유리수 a/b는 곱셈의 역(multiplicative inverse)을 가지며, 역시 그것의 역수(reciprocal)라고 불립니다:
\(\quad\)\(\displaystyle \left(\frac{a}{b}\right)^{-1} = \frac{b}{a}. \)
만약 a/b가 정식의 형식에 있으면, 그것의 역수의 정식의 형식은 a의 부호에 따라 \(b/a\) 또는 \(-b/-\!a\)입니다.
Division
만약 b, c, 및 d가 비-영이면, 나눗셈 규칙은 다음입니다:
\(\quad\)\(\displaystyle \frac{\frac{a}{b}} {\frac{c}{d}} = \frac{ad}{bc}.\)
따라서, a/b를 c/d로 나누는 것은 a/b에 c/d의 역수(reciprocal)를 곱하는 것과 동등합니다:
\(\quad\)\(\displaystyle \frac{ad}{bc} = \frac{a}{b} \cdot \frac{d}{c}.\)
Exponentiation to integer power
만약 n이 비-음의 정수이면, 다음입니다:
\(\left(\displaystyle \frac{a}{b}\right)^n = \frac{a^n}{b^n}.\)
그 결과는 만약 같은 것이 a/b에 대해 참이면 정식의 형식에 있습니다. 특히,
\(\left(\displaystyle \frac{a}{b}\right)^0 = 1.\)
만약 a ≠ 0이면, 다음입니다:
\(\left(\displaystyle \frac{a}{b}\right)^{-n} = \frac{b^n}{a^n}.\)
만약 a/b가 정식의 형식에 있으면, 결과의 정식의 형식은 만약 a > 0 또는 n 중 하나가 짝수이면 \(\frac{b^n}{a^n}\)입니다. 그렇지 않으면, 결과의 정식의 형식은 \(\frac{-b^n}{-a^n}\)입니다.
Continued fraction representation
유한 연속된 분수(finite continued fraction)는 다음을 만족하는 표현입니다:
\(\quad\)\(\displaystyle a_0 + \cfrac{1}{a_1 + \cfrac{1}{a_2 + \cfrac{1}{ \ddots + \cfrac{1}{a_n} }}},\)
여기서 \(a_n\)은 정수입니다. 모든 각 유리수 a/b는 유한 연속된 분수로 묘사될 수 있으며, 그것의 계수(coefficient) \(a_n\)는 (a,b)에 유클리드 알고리듬(Euclidean algorithm)을 적용함으로써 결정될 수 있습니다.
Other representations
- 공통 분수(common fraction): \(\displaystyle \frac{8}{3}\)
- 혼합된 숫자-표시(mixed numeral): \(2\tfrac{2}{3}\)
- 괄선(vinculum)을 사용하여 반복하는 십진(repeating decimal): \(2.\overline{6}\)
- 괄호(parentheses)을 사용하여 반복하는 십진: \(2.(6)\)
- 전통적인 타이포그래피를 사용하여 연속된 분수(continued fraction): \(\displaystyle 2 + \cfrac{1}{1 + \cfrac{1}{2} }\)
- 축약된 표기법에서 연속된 분수: [2; 1, 2]
- 이집트 분수(egyptian fraction): \(\displaystyle 2 + \frac{1}{2} + \frac{1}{6} \)
- 소수 거듭제곱 분해(prime power decomposition): \(2^3\times3^{-1}\)
- 인용-부호 표기법(quote notation): 3'6
위의 것은 같은 유리 값을 표현하기 위한 다른 방법입니다.
Formal construction

유리수는 정수(integer)의 순서화된 쌍(ordered pair)의 동치 클래스(equivalence class)로 구축될 수 있습니다.
보다 정확하게, (Z × (Z \ {0}))를 n ≠ 0을 만족하는 정수의 쌍 (m, n)의 집합으로 놓습니다. 동치 관계(equivalence relation)는 다음에 의해 이 집합 위에 정의됩니다:
\(\quad\)\(\left(m_1, n_1 \right) \sim \left(m_2, n_2 \right) \iff m_1 n_2 = m_2 n_1.\)
덧셈과 곱셈은 다음 규칙에 의해 정의될 수 있습니다:
\(\quad\)\(\left(m_1, n_1\right) + \left(m_2, n_2\right) \equiv \left(m_1n_2 + n_1m_2, n_1n_2\right),\)
\(\quad\)\(\left(m_1, n_1\right) \times \left(m_2, n_2\right) \equiv \left(m_1m_2, n_1n_2\right).\)
이 동치 관계는 합동 관계(congruence relation)이며, 그것이 위에 정의된 덧셈과 곱셈에 호환됨을 의미합니다; 유리수 Q의 집합은, 위의 연산에 의해 유도된 덧셈과 곱셈이 장착된, 동치 관계, (Z × (Z \ {0})) / ~에 의한 몫 집합(quotient set)으로 정의됩니다. (이 구성은 임의의 정수 도메인(integral domain)으로 수행될 수 있고 그것의 분수의 필드(field of fractions)를 생성합니다.)
쌍 (m, n)의 동치 클래스는 \(\displaystyle \frac mn\)으로 표시됩니다. 두 쌍 \((m_1,n_1)\)와 \((m_2,n_2)\)가 같은 동치 클래스에 속하는 것 (즉 동등한 것)과 \(m_1n_2=m_2n_1\)인 것은 필요충분 조건입니다. 이것은 \(\displaystyle \frac{m_1}{n_1}=\frac{m_2}{n_2}\)인 것과 \(m_1n_2=m_2n_1\)인 것은 필요충분 조건임을 의미합니다.
모든 각 동치 클래스 \(\frac mn\)는 무한하게 많은 쌍에 의해 표현될 수 있는데, 왜냐하면 다음이기 때문입니다:
\(\quad\)\(\displaystyle \cdots = \frac{-2m}{-2n} = \frac{-m}{-n} = \frac{m}{n} = \frac{2m}{2n} = \cdots.\)
각 동치 클래스는 고유한 정식의 대표 원소(canonical representative element)를 포함합니다. 정식의 대표는 m과 n이 서로소(coprime)이고 n > 0을 만족하는 동치 클래스에서 고유한 쌍 (m, n)입니다. 그것은 유리수의 가장-낮은 항에서 대표라고 불립니다.
정수는 유리수 \(\displaystyle \frac n1\)을 갖는 정수 n을 식별하여 유리수로 고려될 수 있습니다.
전체 순서(total order)는 유리수에서 정의될 수 있으며, 그것은 정수의 자연스러운 순서를 확장합니다. 우리는 만약 다음이면 \(\displaystyle \frac{m_1}{n_1}\le\frac{m_2}{n_2}\)를 가집니다:
\(\quad\)\((m_1n_2 \le n_1m_2 \quad\text{if}\quad n_1n_2>0)\quad \text{or}\quad (m_1n_2 \ge n_1m_2 \quad\text{if} \quad n_1n_2 < 0).\)
Properties

모든 유리수의 집합 Q는, 위에서 보인 덧셈과 곱셈 연산과 함께, 필드(field)를 형성합니다.
Q는 항등 이외의 필드 자기-동형(field automorphism)을 가지지 않습니다.
위에 정의된 순서와 함께, Q는 자체 이외의 부분필드를 가지지 않는 순서화된 필드(ordered field)이고, 모든 각 순서화된 필드가 Q에 동형(isomorphic)인 고유한 부분필드를 포함한다는 의미에서 가장-작은 순서화된 필드입니다.
Q는 소수 필드(prime field)이며, 이것은 자체 이외의 부분필드를 가지지 않는 필드입니다. 유리수는 특성(characteristic) 영을 갖는 가장-작은 필드입니다. 특성 영의 모든 각 필드는 Q에 동형인 고유한 부분필드를 포함합니다.
Q는 정수(integer) Z의 분수의 필드(field of fractions)입니다. Q의 대수적 클로저(algebraic closure), 즉, 유리 다항식의 근의 필드는 대수적 숫자(algebraic number)의 필드입니다.
모든 유리수의 집합은 셀-수-있는(countable) 것이지만, 모든 실수의 집합 (마찬가지로 무리수의 집합)은 셀-수-없는 것입니다. 셀 수 있는 것, 유리수의 집합은 널 집합(null set)입니다. 즉, 르베그 측정(Lebesgue measure)의 의미에서 거의 모든(almost all) 실수는 무리수입니다.
유리수는 조밀하게 순서화된(densely ordered) 집합입니다: 임의의 두 유리수 사이에, 또 다른 유리수가 놓일 수 있고, 따라서 무한하게 많은 다른 유리수가 놓일 수 있습니다. 예를 들어, 다음을 만족하는 임의의 두 분수에 대해
\(\quad\)\(\displaystyle \frac{a}{b} < \frac{c}{d}\)
(여기서 \(b,d\)는 양수입니다), 우리는 다음을 가집니다:
\(\quad\)\(\displaystyle \frac{a}{b} < \frac{a + c}{b + d} < \frac{c}{d}.\)
셀-수-있는, (위의 의미에서) 조밀하고, 최소 또는 최대 원소를 가지지 않는, 임의의 전체적으로 순서화된(totally ordered) 집합은 유리수에 순서 동형(order isomorphic)입니다.
Real numbers and topological properties
유리수는 실수의 조밀한 부분집합(dense subset)입니다: 모든 각 실수는 그것에 임의적으로 가까운 유리수를 가집니다. 관련된 속성은 유리수가 정규 연속된 분수(regular continued fractions)로 유한(finite) 전개를 갖는 유일한 숫자라는 것입니다.
그것들의 순서의 힘으로, 유리수는 순서 토폴로지(order topology)를 수반합니다. 유리수는, 실수의 부분공간으로, 역시 부분공간 토폴로지(subspace topology)를 수반합니다. 유리수는 절대 차이(absolute difference) 메트릭 d(x,y) = |x − y|을 사용함으로써 메트릭 공간(metric space)을 형성하고, 이것은 Q에 대한 세 번째 토폴로지를 산출합니다. 모든 세 토폴로지가 일치하고 유리수를 토폴로지적 필드(topological field)로 바꿉니다. 유리수는 지역적으로 컴팩트(locally compact)가 아닌 공간의 중요한 예제입니다. 유리수는 고립된 점(isolated point)없이 고유한 셀-수-있는(countable) 메트릭-가능 공간(metrizable space)으로 토폴로지적으로 특성화됩니다. 그 공간은 역시 전체적으로 분리(totally disconnected)됩니다. 유리수는 완비 메트릭 공간(complete metric space)을 형성하지 않습니다; 실수(real numbers)는 위의 메트릭 d(x,y) = |x − y| 아래에서 Q의 완비입니다.
p-adic numbers
위에서 언급된 절댓값 메트릭 외에도, Q를 토폴로지적 필드로 바꾸는 다른 메트릭이 있습니다:
p를 소수(prime number)로 놓고, 임의의 비-영 인수에 대해, \(|a|_p = p^{-n}\)라고 놓으며, 여기서 \(p^n\)은 a를 나누는(dividing) p의 가장-높은 거듭제곱입니다.
게다가 \(|0|_p = 0\)라고 설정합니다. 임의의 유리수 a/b에 대해, 우리는 \(|a/b|_p = |a|_p / |b|_p\)라고 설정합니다.
그런-다음 \(d_p(x,y)=|x-y|_p\)는 Q 위에 메터릭(metric)을 정의합니다.
메트릭 공간 \((\mathbf{Q},d_p)\) (Q,dp)는 완비가 아니고, 그것의 완비는 p-진수 숫자 필드(p-adic number field) \(\mathbf{Q}_p\)입니다. 오스트롭스키의 정리(Ostrowski's theorem)는 유리수 Q 위의 임의의 비-자명한 절댓값(absolute value)은 보통 실수 절댓값 또는 p-진수(p-adic) 절댓값 중에 하나와 동등하다는 것입니다.
External links
- "Rational number", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- "Rational Number" From MathWorld – A Wolfram Web Resource



