Original article: w:Sine and cosine
수학(mathematics)에서, 사인(sine)과 코사인(cosine)은 각도의 삼각 함수(trigonometric function)입니다. 예리한 각도의 사인과 코사인은 직각 삼각형(right triangle)의 문맥에서 정의됩니다: 지정된 각도에 대해, 그것의 사인은 삼각형의 가장-긴 변 (빗변(hypotenuse))의 길이에 대한 해당 각도와 반대쪽인 변의 길이의 비율이고, 코사인은 빗변(hypotenuse)의 길이에 대한 인접 다리 변의 길이의 비율(ratio)입니다. 각도 \(\theta\)에 대해, 사인과 코사인 함수는 \(\sin \theta\)와 \(\cos \theta\)로 표시됩니다.
사인과 코사인의 정의는 단위 원(unit circle)에서 특정 선분의 길이의 관점에서 임의의 실수(real) 값으로 확장되어 왔습니다. 보다 현대적인 정의는 무한 수열(infinite series), 또는 특정 미분 방정식(differential equation)의 해로 사인과 코사인을 표현하며, 임의적인 양 및 음의 값과 심지어 복소수(complex number)까지 그것들의 확장을 허용합니다.
사인과 코사인 함수는 음파 및 광파, 조화 진동자의 위치와 속도, 햇빛 강도와 날 길이, 및 일년 동안 평균 온도 변화와 같은, 주기적(periodic) 현상을 모델링하기 위해 공통적으로 사용됩니다. 함수 사인은, 산스크리트어에서 아랍어로 번역되고, 그런-다음 아랍어에서 라틴어로 번역을 통해, 그것들은 굽타 시대(Gupta period) 동안 인도 천문학(Indian astronomy)에서 사용된 jyā 및 koti-jyā 함수로 거슬러 올라갈 수 있습니다.
Notation
사인과 코사인은 약어 sin과 cos를 갖는 함수형 표기법(functional notation)을 사용하여 작성됩니다.
종종, 인수가 충분히 단순하면, 함수 값은 괄호 없이 sin(θ)가 아닌 sin θ로 작성될 것입니다.
사인과 코사인의 각각은 각도의 함수이며, 이는 보통 라디안(radians) 또는 도(degrees)로 표현됩니다. 달리 명시적으로 언급된 경우를 제외하고, 이 기사는 각도가 라디안에서 측정된다고 가정합니다.
Definitions
Right-angled triangle definitions
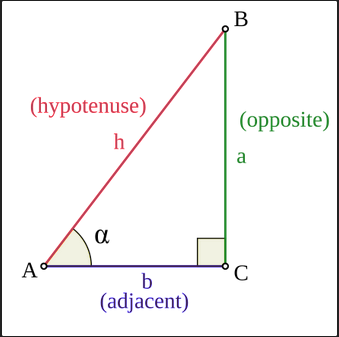
예리한 각도 α의 사인과 코사인 함수를 정의하기 위해, 측정 α의 각도를 포함하는 직각 삼각형(right triangle)으로 시작합니다; 첨부된 그림에서, 삼각형 ABC에서 각도 α는 관심의 각입니다. 삼각형의 세 변은 다음으로 이름짓습니다:
- 반대 변(opposite side)은 관심의 각에 맞은 편 변이며, 이 경우에서 변 a입니다.
- 빗변(hypotenuse)은 직각의 맞은 편 변이며, 이 경우에서 h입니다. 빗변은 직각 삼각형에서 항상 가장-긴 변입니다.
- 인접 변(adjacent side)은 남아있는 변이며, 이 경우에서 b입니다. 그것은 관심의 각 (각도 A)와 직각 둘 다(에 인접한)의 변을 형성합니다.
한번 그러한 삼각형이 선택되면, 각도의 사인은 반대 변의 길이를 빗변의 길이로 나눈 값과 같고, 각도의 코사인은 인접 변의 길이를 빗변의 길이로 나눈 값과 같습니다:
\(\displaystyle\sin(\alpha) = \frac {\textrm{opposite}} {\textrm{hypotenuse}}\qquad\cos(\alpha) = \frac {\textrm{adjacent}} {\textrm{hypotenuse}}\)
각도의 다른 삼각 함수는 유사하게 정의될 수 있습니다; 예를 들어, 탄젠트(tangent)는 반대 변과 인접 변 사이의 비율입니다.
언급된 바와 같이, 값 \(\sin(\alpha)\)와 \(\cos(\alpha)\)는 측정 α의 각도를 포함하는 직각 삼각형의 선택에 의존하는 것으로 보입니다. 어쨌든, 이것은 그 경우가 아닙니다: 모든 그러한 삼각형은 닮은(similar) 것이고, 따라서 그 비율은 그들의 각각에 대해 같습니다.
Unit circle definitions
삼각법(trigonometry)에서, 단위 원(unit circle)은 데카르트 좌표 시스템(Cartesian coordinate system)에서 원점 (0, 0)에 중심을 둔 반지름 일의 원입니다.
x-축의 양의 절반과 θ의 각도를 이루는, 원점을 통과하는 직선이 단위 원과 교차한다고 놓습니다. 이 교차 점의 x- 및 y-좌표는 각각 cos(θ) 및 sin(θ)와 같습니다. 이 정의는 \(0 < \theta < \frac{\pi}{2}\)일 때 사인과 코사인의 직각 삼각형 정의와 일치합니다: 왜냐하면 단위 원의 빗변의 길이가 항상 1이기 때문이며, 즉, \(\sin(\theta) = \frac {\text{opposite}} {\text{hypotenuse}} = \frac {\text{opposite}} {1} = {\text{opposite}}\). 삼각형의 반대 변의 길이는 단순히 y-좌표입니다. 유사한 논증은 코사인 함수에 대해 만들어질 수 있으며, 즉, \(0 < \theta < \frac{\pi}{2}\)일 때, 심지어 단위 원을 사용하는 정의 아래에서도 \(\cos (\theta) = \frac {\text{adjacent}}{\text{hypotenuse}}\)입니다. tan(θ)는 그런-다음 \(\frac{\sin(\theta)}{\cos(\theta)}\), 또는, 동등하게, 선분의 기울기로 정의됩니다.
단위 원(unit circle) 정의를 사용하는 것은 각도가 임의의 실수 인수로 확장될 수 있다는 이점을 가집니다. 이것은 특정 대칭을 요구함으로써 달성될 수 있고, 해당 사인은 주기 함수(periodic function)일 것입니다.
Complex exponential function definitions
지수 함수(exponential function) \(e^z\)는 복소수(complex numbers)의 전체 도메인에서 정의됩니다. 사인과 코사인의 정의는 다음을 통해 모든 복소수로 확장될 수 있습니다:
\(\displaystyle\sin z = \frac{e^{iz} - e^{-iz}}{2i}\)
\(\displaystyle\cos z = \frac{e^{iz} + e^{-iz}}{2}\)
이것들은 다음 오일러의 공식(Euler's formula)을 얻기 위해 역전될 수 있습니다:
\(\displaystyle e^{iz} = \cos z + i \sin z\)
\(\displaystyle e^{-iz} = \cos z - i \sin z\)
복소 평면(complex plane)에 그려질 때, \(x\)의 실수 값에 대해 함수 \(e^{ix}\)는 복소 평면에서 단위 원(unit circle)을 추적합니다.
\(x\)가 실수일 때, 사인과 코사인은 다음으로 \(e^{ix}\) 또는 \(e^{-ix}\)의 허수 부분과 실수 부분으로 단순화됩니다:
\(\sin x = \operatorname{Im}(e^{ix}) = -\operatorname{Im}(e^{-ix})\)
\(\cos x = \operatorname{Re}(e^{ix}) = \operatorname{Re}(e^{-ix})\)
실수 값 \(x\)와 \(y\)에 대해 \(z=x+iy\)일 때, 사인과 코사인은 다음으로 사인, 코사인, 및 쌍곡선 함수(hyperbolic functions)의 관점에서 표현될 수 있습니다:
\(\begin{align}\sin z &= \sin x \cosh y + i \cos x \sinh y\\[5pt]
\cos z &= \cos x \cosh y - i \sin x \sinh y\end{align}\)
Differential equation definition
\((\cos \theta, \sin \theta)\)는 초기 조건(initial conditions) \(y(0) = 0\)과 \(x(0) = 1\)를 갖는 이-차원 미분 방정식(differential equations)의 시스템 \(y'(\theta) = x(\theta)\)과 \(x'(\theta) = -y(\theta)\)에 대한 해 \((x(\theta), y(\theta))\)입니다. 우리는 위 정의에서 단위원을 주어진 초기 조건을 갖는 미분 방정식의 위상 공간 궤적(phase space trajectory)을 정의하는 것으로 해석할 수 있습니다.
이는 초기 조건 \(y(0) = 0\)와 \(x(0) = 1\)에서 시작하여 미분 방정식의 시스템 \(y'(\theta) = x(\theta)\)와 \(x'(\theta) = -y(\theta)\)의 위상 공간 궤적으로 해석될 수 있습니다. (0)=1.
Series definitions
영에서 평가된 사인의 연속 도함수는 그것의 테일러 급수를 결정하기 위해 사용될 수 있습니다. 기하학과 극한(limit)의 속성만을 사용하여, 사인의 도함수(derivative)는 코사인이고, 코사인의 도함수는 사인의 음수임을 알 수 있습니다. 이는 sin(x)의 연속 도함수가 cos(x), -sin(x), -cos(x), sin(x)이며, 그것들 네 개의 함수를 계속 반복한다는 의미입니다. 점 0에서 평가된 (4n+k)-번째 도함수:
\(\sin^{(4n+k)}(0)=\begin{cases}
0 & \text{when } k=0 \\
1 & \text{when } k=1 \\
0 & \text{when } k=2 \\
-1 & \text{when } k=3
\end{cases}\)
여기서 위첨자는 반복된 미분을 나타냅니다. 이는 x = 0에서 다음 테일러 급수 전개를 의미합니다. 그런-다음 테일러 급수(Taylor series)의 이론을 사용하여 다음 항등식이 모든 실수 x (여기서 x는 라디안에서 각도)에 대해 유지되고, 더 일반적으로는 모든 복소수에 대해 유지됨을 보여줄 수 있습니다:
\(\begin{align}
\sin(x)
&= x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} + \cdots \\[5mu]
&= \sum_{n=0}^\infty \frac{(-1)^n}{(2n+1)!}x^{2n+1}
\end{align}\)
각 항의 도함수를 취하는 것은 코사인에 대한 테일러 급수를 제공됩니다:
\(\begin{align}
\cos(x)
&= 1 - \frac{x^2}{2!} + \frac{x^4}{4!} - \frac{x^6}{6!} + \cdots \\[5mu]
&= \sum_{n=0}^\infty \frac{(-1)^n}{(2n)!}x^{2n}
\end{align}\)
이들 테일러 급수는 기본 산술 연산의 측면에서 사인과 코사인의 명시적, 계산-가능한(computable) 정의를 제공합니다.
Continued fraction definitions
사인 함수는 일반화된 연속된 분수(generalized continued fraction)로 표현될 수도 있습니다:
\( \sin(x) =
\cfrac{x}{1 + \cfrac{x^2}{2\cdot3-x^2 +
\cfrac{2\cdot3 x^2}{4\cdot5-x^2 +
\cfrac{4\cdot5 x^2}{6\cdot7-x^2 + \ddots}}}}.
\)
\( \cos (x) = \cfrac{1}{1 + \cfrac{x^2}{1 \cdot 2 - x^2 + \cfrac{1 \cdot 2x^2}{3 \cdot 4 - x^2 + \cfrac{3 \cdot 4x^2}{5 \cdot 6 - x^2 + \ddots}}}}.\)
연속된 분수 표현은 오일러의 연속된 분수 공식(Euler's continued fraction formula)에서 파생될 수 있고 사인과 코사인 함수의 유리수와 무리수 둘 다, 즉 실수 값을 표현할 수 있습니다.
Identities
정확한 항등식 (라디안(radians)을 사용):
이것들은 \(\theta\)의 모든 값에 적용됩니다.
\(\displaystyle\sin(\theta) = \cos\left(\frac{\pi}{2} - \theta \right) = \cos\left(\theta - \frac{\pi}{2}\right)\)
\(\displaystyle\cos(\theta) = \sin\left(\frac{\pi}{2} - \theta \right) = \sin\left(\theta + \frac{\pi}{2}\right)\)
Reciprocals
사인의 역수(reciprocal)는 코시컨트입니다. 즉, \(\sin{\theta}\)의 역수는 \(\csc{\theta}\)입니다. 코시컨트는 반대 변의 길이에 대한 빗변의 길이의 비율을 제공합니다. 마찬가지로, 코사인의 역수는 시컨트이며, 이는 인접 변의 길이에 대한 빗변의 길이의 비율을 제공합니다.
\(\displaystyle\csc{\theta} = \frac{1}{\sin{\theta}} = \frac {\textrm{hypotenuse}} {\textrm{opposite}} \)
\(\displaystyle\sec{\theta} = \frac{1}{\cos{\theta}} = \frac {\textrm{hypotenuse}} {\textrm{adjacent}} \)
Inverses
사인의 역함수(inverse function)는 아크사인 (arcsin 또는 asin) 또는 역 사인 (\(\sin^{-1}\))입니다. 코사인의 역함수는 아크코사인 (arccos, acos, 또는 \(\cos^{-1}\))입니다. (\(\sin^{-1}\)과 \(\cos^{-1}\)에서 −1의 위첨자는 함수의 역을 나타내며, 지수(exponentiation)가 아닙니다.) 사인과 코사인은 단사(injective)가 아니므로, 그것들의 역은 정확한 역함수가 아니라, 부분 역함수입니다. 예를 들어, sin(0) = 0이지만, 역시 sin(π) = 0, sin(2π) = 0 등입니다. 아크사인 함수가 여러-값임이 따라옵니다: arcsin(0) = 0이지만, 역시 arcsin(0) = π, arcsin(0) = 2π, 등입니다. 오직 하나의 값이 요구될 때, 함수는 그것의 주요 가지(principal branch)로 제한될 수 있습니다. 이 제한과 함께, 도메인에서 각 x에 대해, 표현 arcsin(x)는, 그것의 주요 값(principal value)으로 불리는, 오직 단일 값으로 평가할 것입니다. arcsin에 대해 주요 값의 표준 치역은 −π/2에서 π/2이고 arccos에 대해 표준 치역은 0에서 π입니다.
\(\displaystyle\theta = \arcsin \left( \frac{\text{opposite}}{\text{hypotenuse}} \right) = \arccos \left( \frac{\text{adjacent}}{\text{hypotenuse}} \right).\)
여기서 (일부 정수 k에 대해):
\(\begin{align}
\sin(y) = x \iff & y = \arcsin(x) + 2\pi k , \text{ or }\\
& y = \pi - \arcsin(x) + 2\pi k\\
\cos(y) = x \iff & y = \arccos(x) + 2\pi k , \text{ or }\\
& y = - \arccos(x) + 2\pi k
\end{align}\)
정의에 의해, arcsin과 arccos은 다음 방정식을 만족시킵니다:
\(\displaystyle\sin(\arcsin(x)) = x \qquad \cos(\arccos(x)) = x\)
그리고
\(\begin{align}\arcsin(\sin(\theta)) = \theta\quad & \text{for}\quad -\frac{\pi}{2} \leq \theta \leq \frac{\pi}{2}\\
\arccos(\cos(\theta)) = \theta\quad & \text{for}\quad 0 \leq \theta \leq \pi\end{align}\)
Pythagorean trigonometric identity
사인과 코사인 사이의 기본 관계는 피타고라스 삼각 항등식(Pythagorean trigonometric identity)입니다:
\(\displaystyle\cos^2(\theta) + \sin^2(\theta) = 1\)
여기서 \(\sin^2(x)\)는 \((\sin(x))^2\)을 의미합니다.
Double angle formulas
사인과 코사인은 다음 두배 각도 공식을 만족시킵니다:
\(\displaystyle\sin(2\theta) = 2\sin(\theta)\cos(\theta)\)
\(\displaystyle\cos(2\theta) = \cos^2(\theta) - \sin^2(\theta) = 2\cos^2(\theta) - 1 = 1 - 2\sin^2(\theta)\)
코사인 두배 각도 공식은 \(\sin^2\)과 \(\cos^2\)은, 자체로, 이동되고 스케일된 사인 파동임을 의미합니다. 구체적으로,
\(\displaystyle\sin^2(\theta) = \frac{1 - \cos(2\theta)}{2}\qquad\cos^2(\theta) = \frac{1 + \cos(2\theta)}{2}\)
그래프는 사인 함수와 사인 제곱된 함수를 모두 표시하며, 사인은 파란색으로, 사인 제곱된 것은 빨간색으로 표시됩니다. 두 그래프 모두는 같은 모양을 가지지만, 다른 값의 치역을 가지고, 다른 주기를 가집니다. 사인 제곱된 것은 양수 값만 가지지만, 두 배 주기를 가집니다.
Derivative and integrals
사인과 코사인의 도함수는 다음입니다:
\(\displaystyle\frac{d}{dx}\sin(x) = \cos(x) \qquad \frac{d}{dx}\cos(x) = -\sin(x)\)
그리고 그것들의 역도함수는 다음입니다:
\(\displaystyle\int \sin(x)\,dx = -\cos(x) + C \)
\(\displaystyle\int \cos(x)\,dx = \sin(x) + C \)
여기서 C는 적분의 상수(constant of integration)를 나타냅니다.
Properties relating to the quadrants
아래 테이블은, 인수의 사분면에 의해 정렬된, 사인 함수의 여러 주요 속성 (부호, 단조성, 볼록성)을 표시합니다. 테이블에서 그것들 밖의 인수에 대해, 우리는 사인 함수의 주기성 \(\sin(\alpha + 2\pi) = \sin(\alpha)\)을 사용함으로써 대응하는 정보를 계산할 수 있습니다.

다음 테이블은 사분면의 경계에서 기본 정보를 제공합니다.

Fixed points
영은 사인 함수의 유일한 실수 고정된 점(fixed point)입니다; 다시 말해서, 사인 함수와 항등 함수(identity function)의 유일한 교차점은 \(\sin(0)=0\)입니다. 코사인 함수의 유일한 실수 v 불립니다. 즉, 도티 숫자는 \( \cos (x) = x\) 방정식의 고유한 실수 근입니다. 도티 숫자의 십진 전개는 \(0.739085\ldots\)입니다.
Arc length
\(0\)과 \(t\) 사이의 사인 곡선의 호 길이(arc length)는 다음입니다:
\(\displaystyle \int_0^t\!\sqrt{1+\cos^2(x)}\, dx =\sqrt{2} \operatorname{E}(t,1/\sqrt{2}),\)
여기서 \(\operatorname{E}(\varphi,k)\)는 모듈러스 \(k\)를 갖는 두 번째 종류의 불완전 타원 적분(incomplete elliptic integral of the second kind)입니다. 그것은 기본 함수(elementary functions)를 사용하여 표현될 수 없습니다.
전체 주기에 대해 호 길이는 다음입니다:
\(\displaystyle L = \frac{4\sqrt{2\pi ^3}}{\Gamma(1/4)^2} + \frac{\Gamma(1/4)^2}{\sqrt{2\pi}} = \frac{2\pi}{\varpi}+2\varpi = 7.640395578\ldots\)
여기서 \(\Gamma\)는 감마 함수(gamma function)이고 \(\varpi\)는 렘니스케이트 상수(lemniscate constant)입니다.
Laws
사인의 법칙(law of sines)은 변 a, b, 및 c와 그것들 변의 반대쪽 각도 A, B 및 C를 갖는 임의적인 삼각형(triangle)에 대해 다음임을 말합니다:
\(\displaystyle\frac{\sin A}{a} = \frac{\sin B}{b} = \frac{\sin C}{c}.\)
이것은 아래 첫 번째 세 표현의 상등과 동등합니다:
\(\displaystyle\frac{a}{\sin A} = \frac{b}{\sin B} = \frac{c}{\sin C} = 2R,\)
여기서 R은 삼각형의 둘레-반지름(circumradius)입니다.
그것은 삼각형을 두 개의 직각 삼각형으로 나누고 위의 사인의 정의를 사용함으로써 입증될 수 있습니다. 사인의 법칙은, 만약 두 각도와 한 변이 알려져 있으면, 삼각형에서 미지수 변의 길이를 계산하는 데 유용합니다. 이것은 삼각분할(triangulation), 두 각도와 접근-가능한 둘러싸인 거리를 측정함으로써 미지수 거리를 결정하기 위한 기법에서 발생하는 공통 상황입니다.
코사인의 법칙(law of cosines)은 변 a, b, 및 c와 그것들 변의 반대쪽 각도 A, B, 및 C를 갖는 임의적인 삼각형에 대해 다음임을 말합니다:
\(\displaystyle a^2 + b^2 - 2ab\cos(C) = c^2\)
\(C = \pi/2\)인 경우에서, \(\cos(C) = 0\)이고 이것은 피타고라스 정리(Pythagorean theorem)가 됩니다: 직각 삼각형에 대해, \(a^2 + b^2 = c^2\)이며, 여기서 c는 빗변입니다.
Special values
각도의 특정 정수에 대해, sin(x)의 값이 특히 간단합니다. 이들 값의 일부의 테이블은 아래에 제공됩니다.
15° (즉, \(\textstyle\frac\pi{12}\) 라디안)의 정수 배수(integer multiples)에 대해, sin(x)와 cos(x)의 값은 특히 단순하고 오직 \(\sqrt 2,\sqrt 3, \sqrt 6\)의 항으로 표현될 수 있습니다. 이들 각도의 테이블은 아래에 제공됩니다. 보다 복잡한 각도에 대해 Exact trigonometric values § Common angles를 참조하십시오.

90도씩 증가:

Relationship to complex numbers
사인과 코사인은 그것의 극 좌표(polar coordinates) (r, φ)를 갖는 복소수(complex number)의 실수 부분과 허수 부분(imaginary part)을 연결하기 위해 사용됩니다:
\( z = r(\cos(\varphi) + i\sin(\varphi))\)
실수 부분과 허수 부분은 다음입니다:
\(\operatorname{Re}(z) = r \cos(\varphi)\)
\(\operatorname{Im}(z) = r \sin(\varphi)\)
여기서 r과 φ는 복소수 z의 크기와 각도를 나타냅니다.
임의의 실수 θ에 대해, 오일러의 공식(Euler's formula)은 다음임을 말합니다:
\(e^{i\theta} = \cos(\theta) + i \sin(\theta)\)
그러므로, 만약 z의 극 좌표가 (r, φ)이면, \(z = re^{i\varphi}\)입니다.
Complex arguments
사인과 코사인의 급수 정의를 복소 인수, z에 적용하는 것은 다음을 제공합니다:
\(\begin{align}
\sin(z)& = \sum_{n=0}^\infty \frac{(-1)^n}{(2n+1)!}z^{2n+1} \\
& = \frac{e^{i z} - e^{-i z}}{2i} \\
& = \frac{\sinh \left( i z\right) }{i} \\
& = -i \sinh \left(i z\right)\\
\cos(z)& = \sum_{n=0}^\infty \frac{(-1)^n}{(2n)!}z^{2n} \\
& = \frac{e^{i z} + e^{-i z}}{2} \\
& = \cosh( i z) \\
\end{align}\)
여기서 sinh와 cosh는 쌍곡 사인과 코사인(hyperbolic sine and cosine)입니다. 이것들은 전체 함수(entire functions)입니다.
그것은 역시 인수의 실수 부분과 허수 부분의 관점에서 복소 사인과 코사인 함수를 표현하기 위해 때때로 유용합니다:
\(\begin{align}
\sin (x + iy) &= \sin(x) \cos(iy) + \cos(x) \sin(iy) \\
&= \sin(x) \cosh(y) + i \cos(x) \sinh(y)\\
\cos (x + iy) &= \cos(x) \cos(iy) - \sin(x) \sin(iy) \\
&= \cos(x) \cosh(y) - i \sin(x) \sinh(y)\\
\end{align}\)
Partial fraction and product expansions of complex sine
복소 해석학(complex analysis)에서 부분 분수 전개 기법을 사용하여, 우리는 다음 무한 급수는
\(\displaystyle\sum_{n = -\infty}^{\infty}\frac{(-1)^n}{z-n} = \frac{1}{z} -2z \sum_{n = 1}^{\infty}\frac{(-1)^n}{n^2 - z^2}\)
둘 다가 수렴하고 \(\frac{\pi}{\sin (\pi z)}\)와 같음을 알 수 있습니다. 비슷하게, 우리는 다음임을 알 수 있습니다:
\(\displaystyle\frac{\pi^2}{\sin^2 (\pi z)} = \sum_{n=-\infty}^\infty \frac{1}{(z - n)^2}.\)
곱 전개 기법을 사용하여, 우리는 다음을 유도할 수 있습니다:
\(\displaystyle\sin(\pi z) = \pi z \prod_{n = 1}^\infty \left( 1 - \frac{z^2}{n^2} \right).\)
대안적으로, 사인에 대해 무한 곱은 복소 푸리에 급수(complex Fourier series)를 사용하여 입증될 수 있습니다.
사인에 대해 무한 곱의 증명
복소 푸리에 급수를 사용하여, 함수 \(\cos (zx)\)는 다음으로 분해될 수 있습니다:
\(\displaystyle\cos (zx) = \frac{z\sin (\pi z)}{\pi}\displaystyle\sum_{n=-\infty}^\infty \frac{(-1)^n \, e^{inx}}{z^2 - n^2}, \, z\in\Complex \setminus \mathbb{Z}, \, x\in [-\pi ,\pi].\)
\(x=\pi\)를 설정하는 것은 다음을 산출합니다:
\(\displaystyle\cos (\pi z) =
\frac{z\sin (\pi z)}{\pi}\displaystyle\sum_{n=-\infty}^\infty \frac{1}{z^2 - n^2} =
\frac{z\sin (\pi z)}{\pi}\left(\frac{1}{z^2} + 2\displaystyle\sum_{n=1}^\infty \frac{1}{z^2 - n^2}\right).
\)
그러므로 우리는 다음을 얻습니다:
\(\displaystyle\pi \cot (\pi z) = \frac{1}{z} + 2\displaystyle\sum_{n=1}^\infty \frac{z}{z^2 - n^2}.\)
함수 \(\pi \cot (\pi z)\)는 \(\ln (\sin (\pi z))+C_0\)의 도함수입니다. 게다가, 만약 \(\frac{df}{dz}=\frac{z}{z^2-n^2}\)이면, \(\mathbb{C}\)의 일부 열린 것이고 연결된 부분집합 위에 드러난 급수가 수렴하는 것을 만족하는 함수 \(f\)는 \(f=\frac{1}{2}\ln (1-z^2/n^2)+C_1\)이며, 이는 바이어슈트라스 M-테스트(Weierstrass M-test)를 사용하여 입증될 수 있습니다. 합과 도함수의 교환은 균등 수렴(uniform convergence)에 의해 정당화됩니다. 그것은 다음임을 따릅니다:
\(\displaystyle\ln (\sin (\pi z)) = \ln (z) + \displaystyle\sum_{n=1}^\infty \ln \left(1 - \frac{z^2}{n^2}\right) + C.\)
지수화는 다음을 제공합니다:
\(\displaystyle\sin (\pi z) = ze^C \displaystyle\prod_{n=1}^\infty \left(1 - \frac{z^2}{n^2}\right).\)
\(\displaystyle\lim_{z\to 0}\frac{\sin (\pi z)}{z} = \pi\)과 \(\lim_{z\to 0}\prod_{n=1}^\infty \left(1 - \frac{z^2}{n^2}\right) = 1\)이므로, \(e^C =\pi\)을 가집니다. 따라서 \(\mathbb{C}\)의 일부 열린 것이고 연결된 부분집합에 대해,
\(\displaystyle\sin (\pi z) = \pi z\displaystyle\prod_{n=1}^\infty \left(1 - \frac{z^2}{n^2}\right)\)
\(a_{n}(z) = -\frac{z^2}{n^2}\)라고 놓습니다. \(\sum_{n=1}^\infty |a_{n}(z)|\)는 임의의 닫힌 디스크 위에 균등하게 수렴(converges uniformly)하므로, \(\prod_{n=1}^\infty (1 + a_{n}(z))\)는 마찬가지로 임의의 닫힌 디스크 위에 균등하게 수렴합니다. 무한 곱은 \(\mathbb{C}\) 위에 정칙임이 따라옵니다. 항등 정리(identity theorem)에 의해, 사인에 대해 무한 곱은 모든 \(z\in\mathbb C\)에 대해 유효하며, 이는 증명을 완성합니다. \(\blacksquare \)
Usage of complex sine
sin(z)는 감마 함수(Gamma function)에 대해 함수형 방정식(functional equation)에서 찾아집니다:
\(\displaystyle\Gamma(s)\Gamma(1 - s) = {\pi\over\sin(\pi s)},\)
이는 차례로 리만 제타-함수(Riemann zeta-function)에 대해 함수형 방정식(functional equation)에서 찾아집니다:
\(\displaystyle\zeta(s) = 2(2\pi)^{s-1}\Gamma(1 - s)\sin\left(\frac{\pi}{2} s\right)\zeta(1 - s).\)
정칙 함수(holomorphic function)이기 때문에, sin z는 라플라스 방정식(Laplace's equation)의 2D 해입니다:
\(\displaystyle\Delta u(x_1, x_2) = 0.\)
복소 사인 함수는 역시 진자(pendulums)의 수준 곡선과 관련됩니다.
History
삼각법의 초기 연구는 고대로 거슬러 올라갈 수 있지만, 그것들이 오늘날 사용되는 것과 같은 삼각 함수(trigonometric functions)는 중세 시대에 개발되었습니다. 현(chord) 함수는 니케아(Nicaea)의 히파르쿠스(Hipparchus) (기원전 180–125) 및 로마 이집트(Roman Egypt)의 프톨레마이오스(Ptolemy) (기원후 90–165)에 의해 발견되었습니다.
사인과 코사인 함수는, 산스크리트어에서 아랍어로 번역되고 그런-다음 아랍어에서 라틴어로 번역을 통해, 굽타 시대(Gupta period) (Aryabhatiya, Surya Siddhanta) 동안 인도 천문학(Indian astronomy)에서 사용된 jyā 및 koti-jyā 함수로 거슬러 올라갈 수 있습니다.
현재 사용되고 있는 모든 여섯 삼각 함수는, 삼각형을 푸는(solving triangles) 데 사용되는 사인의 법칙(law of sines)과 같이, 9세기까지 이슬람 수학(Islamic mathematics)에서 알려져 있었습니다. 사인의 예외와 함께 (이는 인도 수학에서 채택되었습니다), 다른 다섯 개의 현대 삼각 함수는 코사인, 탄젠트, 코탄젠트, 시컨트, 및 코시컨트를 포함하여 아랍 수학자에 의해 발견되었습니다. 알-콰리즈미(Al-Khwārizmī) (c. 780–850)는 사인, 코사인, 및 탄젠트의 테이블을 생성했습니다. 무하미드 이븐 자비르 알-하라니 알-바타니(Muhammad ibn Jābir al-Harrānī al-Battānī) (853—929)는 시컨트와 코시컨트의 역수 함수를 발견했고, 1°에서 90°까지 각 각도에 대해 코시컨트의 첫 번째 테이블을 만들었습니다.
약어 sin, cos, 및 tan의 첫 번째 출판된 사용은 16세기 프랑스 수학자 알버트 지라드(Albert Girard)에 의한 것입니다; 이것들은 오일러에 의해 추가로 공표되었습니다 (아래를 참조하십시오). 코페르니쿠스(Copernicus)의 학생, 게오르크 요하임 레티쿠스(Georg Joachim Rheticus)의 Opus palatinum de triangulis는 모든 여섯 개의 삼각 함수에 대해 테이블을 갖는, 원 대신에 직각 삼각형의 관점에서 직접 삼각 함수를 정의하는 것이 유럽에서 아마도 최초였습니다; 이 연구는 1596년 레티쿠스(Rheticus)의 학생 발렌틴 오소(Valentin Otho)에 의해 완성되었습니다.
1682년에 출판된 논문에서, 라이프니츠(Leibniz)는 sin x가 x의 대수적 함수(algebraic function)가 아님을 입증했습니다. 로저 코츠(Roger Cotes)는 그의 Harmonia Mensurarum (1722)에서 사인의 도함수를 계산했었습니다. 레온하르트 오일러(Leonhard Euler)의 Introductio in analysin infinitorum (1748)는 유럽에서 삼각 함수의 해석적 처리를 설정하고, 역시 이것을 무한 급수로 정의하고 "오일러의 공식(Euler's formula)"을 제시한 것뿐만 아니라, 근-현대 약어 sin., cos., tang., cot., sec., 및 cosec에 대해 대체로 공헌했습니다.
Etymology
단어 sine은, 간접적으로, 원의 호와 그것의 대응하는 현과 활줄을 갖는 활 사이의 시각적 닮음으로 인해 산스크리트(Sanskrit) 단어, jyā '활-줄' 또는 더 구체적으로 그 동의어 jīvá (둘 다 고대 그리스어 χορδή '끈'에서 채택됨)에서 파생됩니다 (jyā, koti-jyā and utkrama-jyā를 참조하십시오). 이것은 아랍어(Arabic)에서 jība로 음역(transliterated)되었으며, 이는 해당 언어에서 의미가 없었고 jb (جب)로 쓰였습니다. 아랍어는 짧은 모음없이 쓰였으므로, jb는 동형-이의어(homograph) jayb (جيب)로 해석되었으며, 이는 'bosom', 'pocket', 또는 'fold'를 의미합니다. 알-바타니(Al-Battani)와 알-콰리즈미(al-Khwārizmī)의 아랍어 텍스트가 크레모나의 제라드(Gerard of Cremona)에 의해 12세기에서 중세 라틴어(Medieval Latin)로 번역될 때, 그는 동등한 라틴어, sinus를 사용했습니다 (이는 역시 'bay' 또는 'fold'를 의미하고, 더 구체적으로 'the hanging fold of a toga over the breast'를 의미합니다). 제라드는 아마도 이 번역을 사용한 최초의 학자가 아니었을 것입니다; 체스터의 로버트가 그보다 앞서-있는 것으로 보이고 심지어 그 이전에 사용된 증거가 있습니다. 영어 형식 sine은 1590년대에 도입되었습니다.
단어 cosine은 에드먼드 건터(Edmund Gunte)의 Canon triangulorum (1620)에서 cosinus로 라틴어 complementi sinus 'sine of the complementary angle'의 약어에서 파생되었으며, 이는 역시 cotangens의 유사한 정의를 포함합니다.
Software implementations
사인과 코사인을 계산하는 데 표준 알고리즘은 없습니다. IEEE 754, 신뢰할 수 있는 부동-점 계산의 사양을 위해 가장 널리 사용되는 표준은 사인과 같은 삼각 함수 계산을 다루지 않습니다. 그 이유는 특히 대규모 입력에 대해 지정된 정확도로 사인과 코사인을 계산하는 데 효율적인 알고리즘이 알려져 있지 않기 때문입니다.
사인을 계산하는 데 알고리즘은 속력, 정확도, 이식성, 또는 허용되는 입력 값의 범위와 같은 제약 조건에 따라 균형을 이룰 수 있습니다. 이것은 특히 매우 큰 입력과 같은 특별한 상황, 예를 들어 \(\sin(10^{22})\)에서 다양한 알고리즘에 대해 다른 결과를 초래할 수 있습니다.
특히 3D 그래픽에 사용되는 공통적인 프로그래밍 최적화는 사인 값의 테이블을 미리 계산하는 것입니다, 예를 들어, 도당 하나의 값, 그런-다음 그것을 근사화하기 그 사이의 값에 대해 가장 가까운 미리-계산된 값을 선택하거나, 그것을 근사화하기 위해 가장 가까운 2개 값 사이를 선형적으로 보간합니다. 이를 통해 결과를 실시간으로 계산하는 대신 테이블에서 조회할 수 있습니다. 최신 CPU 아키텍처와 함께, 이 방법이 아무런 이점을 제공하지 못할 수 있습니다.
CORDIC 알고리즘은 공학용 계산기에서 공통적으로 사용됩니다.
사인과 코사인 함수는, 다른 삼각 함수와 함께, 프로그래밍 언어와 플랫폼에서 광범위하게 사용할 수 있습니다. 컴퓨팅에서, 그것들은 전형적으로 sin과 cos으로 축약됩니다.
일부 CPU 아키텍처는 80387 이래로 인텔 x87 FPU를 포함하여 사인에 대한 내장된 명령어를 가집니다.
프로그래밍 언어에서, sin과 cos은 전형적으로 내장된 함수 또는 언어의 표준 수학 라이브러리에서 찾을 수 있습니다.
예를 들어, C 표준 라이브러리(C standard library)는 math.h 내에 사인 함수를 정의합니다: sin(double), sinf(float), 및 sinl(long double). 각각의 매개변수는 각도를 라디안으로 지정하는 부동-점(floating point) 값입니다. 각 함수는 그것이 허용하는 것과 같은 데이터 형식(data type)을 반환합니다. 많은 다른 삼각 함수는 역시 코사인, 아크 사인, 및 쌍곡 사인 (sinh)와 같은 것에 대해 math.h에 정의되어 있습니다.
비슷하게, 파이썬(Python)은 내장된 math 모듈 내에서 math.sin(x)와 math.cos(x)를 정의합니다. 복소 사인과 코사인 함수는 cmath 모듈, 예를 들어, cmath.sin(z)내에서 역시 유용합니다. CPython의 수학 함수는 C 수학 라이브러리를 호출하고, 두배-정밀도 부동-점 형식을 사용합니다.
Turns based implementations
일부 소프트웨어 라이브러리는 입력 각도를 절반-바퀴(turns)로 사용하여 사인과 코사인의 구현을 제공하며, 절반-바퀴는 180도 또는 \(\pi\) 라디안의 각도입니다. 바퀴 또는 절반-바퀴로 각도를 나타내는 것은 일부 경우에서 정확도 이점과 효율성 이점을 가집니다. MATLAB, OpenCL, R, Julia, CUDA, 및 ARM에서, 이들 함수는 sinpi와 cospi라고 불립니다.. 예를 들어, sinpi(x)는 \(\sin(\pi x)\)로 평가되며, 여기서 x는 반-회전으로 표현되고, 결과적으로 함수에 대한 최종 입력, πx는 sin에 의해 라디안으로 해석될 수 있습니다.
정확도 이점은 이진 부동-점 또는 고정-점에서 한-바퀴, 절반-바퀴, 반의 반 바퀴와 같은 주요 각도를 완벽하게 표현할 수 있는 능력에서 비롯됩니다. 대조적으로, 이진 부동-점 또는 이진 스케일된 고정-점에서 \(2\pi\), \(\pi\), 및 \(\frac{\pi}{2}\)을 나타내는 것은 항상 정확도의 손실을 포함하는데 왜냐하면 무리수는 유한하게 많은 이진 자릿수로 표현될 수 없기 때문입니다.
바퀴는 역시 모듈로를 한 주기로 계산하는 데 정확도 이점과 효율성 이점을 가집니다. 모듈로 1 바퀴 또는 모듈로 2 절반-바퀴를 계산하는 것은 부동-점과 고정-점 둘 다에서 손실없고 효율적으로 계산될 수 있습니다. 예를 들어, 이진-점 스케일된 고정-점 값에 대해 모듈로 1 또는 모듈로 2를 계산하는 것은 오직 비트 이동 또는 비트별 AND 연산을 요구합니다. 반대로, 모듈로 \(\frac{\pi}{2}\)을 계산하는 것은 \(\frac{\pi}{2}\)를 나타내는 것에서 부정확성을 포함합니다.
각도 센서를 포함하는 응용에 대해, 센서는 전형적으로 바퀴 또는 절반-바퀴와 직접 호환되는 형식으로 각도 측정을 제공합니다. 예를 들어, 각도 센서는 한 번의 완전한 회전에 걸쳐 0에서 4096까지 셀 수 있습니다. 만약 절반-바퀴가 각도에 대해 단위로 사용되면, 센서에 의해 제공된 값은 이진 점의 오른쪽에 11 비트를 가진 고정-점 데이터 형식에 직접적으로 및 무손실로 매핑됩니다. 반대로, 만약 라디안이 각도를 저장하는 데 단위로 사용되면, 원시 센서 정수에 \(\frac{\pi}{2048}\)에 대한 근삿값을 곱하는 부정확성과 비용이 발생할 것입니다.
References
- Traupman, Ph.D., John C. (1966), The New College Latin & English Dictionary, Toronto: Bantam, ISBN 0-553-27619-0
- Webster's Seventh New Collegiate Dictionary, Springfield: G. & C. Merriam Company, 1969
External links
- Media related to Sine function at Wikimedia Commons
