물리학(physics)과 수학(mathematics)에서, n 개의 숫자의 수열(sequence)은 n-차원 공간에서 위치를 지정할 수 있습니다. n = 1일 때, 모든 그러한 위치의 집합은 일-차원 공간(space)이라고 불립니다. 일-차원 공간의 예로 숫자 직선(number line)이 있으며, 여기서 각 점의 위치는 단일 숫자로 설명될 수 있습니다.
대수적 기하학(algebraic geometry)에서, 기술적으로는 일-차원 공간이지만 다른 용어로 참조되는 여러 구조가 있습니다. 필드(field) k는 자체에 걸쳐 일-차원 벡터 공간(vector space)입니다. 유사하게, k에 걸쳐 투영 직선(projective line)은 일-차원 공간입니다. 특히, 만약 k = ℂ, 복소수이면, 복소 투영 직선(complex projective line) \(\rm P^1(\mathbb{C})\)은 비록 그것이 리만 구(Riemann sphere)로 알려져 있지만 \(\mathbb{C}\)에 관해 일-차원입니다.
보다 일반적으로, 링(ring)은 자체에 걸쳐 길이-일 모듈(module)입니다. 유사하게, 링에 걸쳐 투영 직선(projective line over a ring)은 링에 걸쳐 일-차원 공간입니다. 링이 필드에 걸쳐 대수(algebra over a field)인 경우에서, 이들 공간은 비록 대수가 더 높은 차원성이더라도 대수에 관해 일-차원입니다.
Hypersphere
1차원에서 초-구(hypersphere)는 한 쌍의 점(points)이며, 때때로 그 표면이 영-차원이기 때문에 0-구(0-sphere)라고 불립니다. 그것의 길이는 다음과 같습니다:
\(\quad\displaystyle L = 2r\)
여기서 \(\displaystyle r\)은 반지름입니다.
Coordinate systems in one-dimensional space
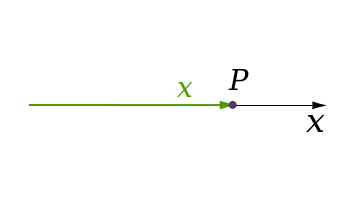
일 차원 좌표 시스템은 숫자 직선(number line)을 포함합니다.
References
- Гущин, Д. Д. "Пространство как математическое понятие" (in Russian). fmclass.ru. Retrieved 2015-06-06.
- Gibilisco, Stan (1983). Understanding Einstein's Theories of Relativity: Man's New Perspective on the Cosmos. TAB Books. p. 89. ISBN 9780486266596.


