절편 정리(intercept theorem)는, 역시 탈레스의 정리(Thales's theorem), 기본 비례성 정리(basic proportionality theorem) 또는 측면 분할 정리(side splitter theorem)라고 알려져 있으며, 공통 시작점을 갖는 두 반직선(ray)이 한 쌍의 평행선(parallels)에 의해 교차되면 생성되는 다양한 선분(line segment)의 비율에 대한 기본 기하학(elementary geometry)의 중요한 정리입니다. 그것은 닮은 삼각형(similar triangles)에서 비율에 대한 정리와 동등합니다. 그것은 전통적으로 그리스 수학자 탈레스(Thales)로 인해 기인합니다. 그것은 고대 바빌로니아인과 이집트인들에게 알려져 있었지만, 처음으로 알려진 증명은 유클리드(Euclid)의 원론(Elements)에 나와 있습니다.
Formulation of the theorem

S가 두 반직선의 공통 시작점이고 두 평행선이 두 반직선과 교차한다고 가정합니다 (그림 참조). A, B를 첫 번째 반직선과 두 평행선의 교차점으로 놓고, B가 A보다 S에서 더 멀리 떨어져 있도록 하고, 마찬가지로 C, D를 두 번째 반직선과 두 평행선의 교차점으로 D가 C보다 S에서 더 멀어지도록 합니다. 이 구성에서는 다음 명제가 유지됩니다:
- 첫 번째 반직선 위의 임의의 두 선분의 비율은 두 번째 반직선 위의 해당 선분의 비율과 같습니다:
- \(\displaystyle \frac{| SA |}{| AB |} =\frac{| SC |}{ | CD |}\), \(\displaystyle\frac{| SB |}{| AB |} =\frac{| SD |}{| CD |} \), \(\displaystyle\frac{| SA |}{| SB |} =\frac{| SC |}{| SD |} \)
- S에서 시작하는 같은 반직선 위의 두 선분의 비율은 평행선 위의 선분의 비율과 같습니다:
- \(\displaystyle \frac{| SA |}{| SB |} = \frac{| SC |}{| SD |} =\frac{| AC |}{| BD |} \)
- 첫 번째 명제의 전환도 마찬가지입니다. 즉, 두 개의 반직선이 두 개의 임의적인 직선에 의해 교차되고 \(\frac{| SA |}{| AB |} =\frac{| SC |}{| CD |} \)가 유지되면 두 개의 교차하는 직선이 평행합니다. 어쨌든, 두 번째 명제의 전환은 사실이 아닙니다 (반대예제에 대해 그래픽를 참조하십시오).
Extensions and conclusions
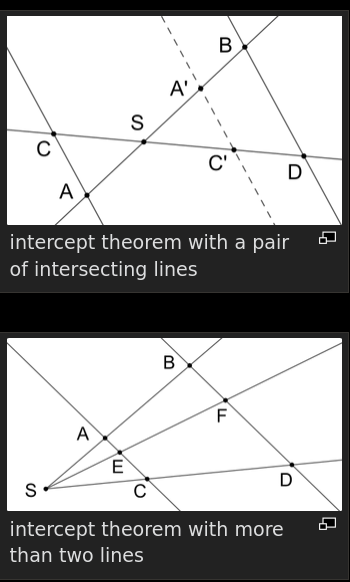
처음 두 명제는 두 반직선이 \(S\)에서 교차하는 두 직선에 의해 대체되면 참을 유지합니다. 이 경우에서, \(S\)와 관련하여 두 가지 시나리오가 있습니다. 그것이 2 평행선 사이에 놓이거나 (X 그림) 그렇지 않은 경우입니다 (V 그림). 만약 \(S\)가 두 평행선 사이에 위치하지 않으면, 원래 정리가 직접 적용됩니다. 만약 \(S\)가 두 평행선 사이에 놓이면, \(S\)에서 \(A\)와 \(C\)의 반사는 원래 정리가 이제 적용되는 동일한 측정값을 갖는 V 그림을 산출합니다. 세 번째 명제 (전환)은 어쨌든 직선에 대해서는 참으로 남지 않습니다.
만약 \(S\)에서 시작하는 두 개보다 많은 반직선 또는 \(S\)에서 교차하는 두 개보다 많은 직선이 있으면 각 평행선은 두 개 이상의 선분을 포함하고 한 평행선 위의 두 선분 비율은 나머지 다른 평행선 위의 해당 선분 비율과 같습니다. 예를 들어 \(S\)에서 시작하여 \(E\)와 \(F\)에서 평행선과 교차하는 세 번째 반직선이 있고, \(F\)가 \(E\)보다 \(S\)에서 더 멀리 떨어져 있으면, 다음 상등이 유지됩니다:
\(\displaystyle \frac{| AE |}{| BF |} =\frac{| EC |}{ | FD |}\) , \(\displaystyle \frac{| AE |}{ | EC |} =\frac{| BF |}{| FD |} \)
두 번째 방정식에 대해 그 전환도 마찬가지로 참입니다. 즉, 3개의 반직선이 두 개의 직선에 의해 교차되고 각 직선 위의 해당 선분의 비율이 같으면, 그것들 두 직선은 평행해야 합니다.
Related concepts
Similarity and similar triangles
절편 정리는 닮음(similarity)과 밀접한 관련이 있습니다. 그것은 닮은 삼각형(similar triangles)의 개념과 동등하며, 즉, 그것은 닮은 삼각형의 성질을 입증하기 위해 사용될 수 있고 닮은 삼각형은 절편 정리를 증명하기 위해 사용될 수 있습니다. 동일한 각도를 일치시킴으로써, 항상 두 개의 유사한 삼각형을 절편 정리가 적용되는 구성을 얻기 위해 서로 배치될 수 있습니다; 그리고 전환적(conversely)으로 절편 정리 구성은 항상 두 개의 닮은 삼각형을 포함합니다.

Scalar multiplication in vector spaces
노름화된 [[vector space|벡터 공간(vector space)]]에서, [[scalar multiplication|스칼라 곱셈(scalar multiplication)]]에 관한 [[axiom|공리]] (특히 \(\lambda \cdot (\vec{a}+\vec{b})=\lambda \cdot \vec{a}+ \lambda \cdot \vec{b}\) 및 \( \|\lambda \vec{a}\|=|\lambda|\cdot\ \|\vec{a}\| \))는 절편 정리가 유지되도록 보장합니다. 우리는 \(
\frac{ \| \lambda \cdot \vec{a} \| }{ \| \vec{a} \|}
=\frac{\|\lambda\cdot\vec{b}\|}{\|\vec{b}\|}
=\frac{\|\lambda\cdot(\vec{a}+\vec{b}) \|}{\|\vec{a}+\vec{b}\|}
=|\lambda|
\)를 가집니다.

Applications
Algebraic formulation of compass and ruler constructions
컴퍼스와 직선자 구성(compass and straightedge constructions)에 관한 그리스인들이 제기한 기본 기하학에는 세 가지 유명한 문제가 있습니다:[6][7]
세 가지 모두가 마침내 불가능하다는 것이 밝혀지기까지는 2000년 이상이 걸렸습니다. 이것은 19세기 당시에 가능했던 대수적 방법의 도움으로 달성되었습니다. 필드 확장(field extensions)을 사용하여 대수적 용어로 세 가지 문제를 재구성하기 위해, 우리는 필드 연산(field operations)을 컴퍼스와 직선자 구성과 일치시켜야 합니다 (구성-가능한 숫자(constructible number) 참조). 특히 두 개의 주어진 선분에 대해, 새로운 선분이 그 길이가 나머지 두 선분의 길이의 곱과 같음을 만족하도록 구성될 수 있음을 보장하는 것이 중요합니다. 유사하게, 우리는 길이 \(a\)의 선분에 대해, 길이 \(a^{-1}\)의 새로운 선분을 구성할 수 있어야 합니다. 절편 정리는 두 경우 모두에 대해, 그러한 구성이 가능하다는 것을 보여주기 위해 사용될 수 있습니다.

Dividing a line segment in a given ratio

Measuring and survey
Height of the Cheops pyramid

일부 역사적 자료에 따르면 그리스 수학자 탈레스(Thales)는 Cheops' pyramid의 높이를 결정하기 위해 절편 정리를 적용했습니다. 다음 설명은 피라미드의 높이를 계산하기 위해 절편 정리의 사용을 설명합니다. 어쨌든, 소실된 탈레스의 원본 연구에 대해서는 언급하지 않습니다.
탈레스는 피라미드 밑면의 길이와 그 기둥의 높이를 측정했습니다. 그런-다음 그는 하루 중 같은 시간에 피라미드 그림자의 길이와 기둥 그림자의 길이를 측정했습니다. 이를 통해 다음과 같은 데이터가 산출되었습니다:
- 기둥의 높이 (A): 1.63 m
- 기둥의 그림자 (B): 2 m
- 피라미드 밑변의 길이: 230 m
- 피라미드의 그림자: 65 m
이것으로부터 그는 계산했습니다
\(\displaystyle C = 65~\text{m}+\frac{230~\text{m}}{2}=180~\text{m}\)
A, B, 및 C를 알게 된 그는 이제 다음으로 절편 정리를 적용하여 계산할 수 있었습니다:
\(\displaystyle D=\frac{C \cdot A}{B}=\frac{1.63~\text{m} \cdot 180~\text{m}}{2~\text{m}}=146.7~\text{m}\)
Measuring the width of a river

Parallel lines in triangles and trapezoids
절편 정리는 특정 구성이 평행 직선 (선분)을 산출한다는 것을 입증하기 위해 사용될 수 있습니다.

Historical aspects
그 정리는 전통적으로 그리스 수학자 밀레토스의 탈레스(Thales of Miletus)로 공인되며, 그는 이집트에서 피라미드의 높이를 결정하고 해안에서 배까지의 거리를 계산하기 위해 정리의 일부 형식을 사용했을 수 있습니다.
Proof
그 정리의 기본 증명은 비율에 대한 기본 명제을 도출하기 위해 같은 넓이의 삼각형을 사용합니다 (주장 1). 그런 다음 첫 번째 주장과 모순을 적용함으로써 다른 주장이 이어집니다.
Claim 1

Claim 2

Claim 3

References
- French, Doug (2004). Teaching and Learning Geometry. BLoomsbury. pp. 84–87. ISBN 9780826473622. (online copy, p. 84, at Google Books)
- Agricola, Ilka; Friedrich, Thomas (2008). Elementary Geometry. AMS. pp. 10–13, 16–18. ISBN 0-8218-4347-8. (online copy, p. 10, at Google Books)
- Stillwell, John (2005). The Four Pillars of Geometry. Springer. p. 34. ISBN 978-0-387-25530-9. (online copy, p. 34, at Google Books)
- Ostermann, Alexander; Wanner, Gerhard (2012). Geometry by Its History. Springer. pp. 3–7. ISBN 978-3-642-29163-0. (online copy, p. 3, at Google Books)
- Lorenz Halbeisen, Norbert Hungerbühler, Juan Läuchli: Mit harmonischen Verhältnissen zu Kegelschnitten: Perlen der klassischen Geometrie. Springer 2016, ISBN 9783662530344, pp. 191–208 (German)
External links
- Intercept Theorem at PlanetMath
- Alexander Bogomolny: Thales' Theorems and in particular Thales' Theorem at Cut-the-Knot
- intercept theorem interactive
