수학(mathematics)에서, 조화 급수(harmonic series)는 다음의 발산하는(divergent) 무한 급수(infinite series)입니다:
\(\quad\displaystyle \displaystyle \sum_{n=1}^\infty\frac{1}{n} = 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + \cdots\).
그의 이름은 음악(music)에서 배음(overtone) 또는 하모닉의 개념으로부터 파생됩니다: 진동하는 현의 배음의 파장(wavelength)은 현의 기본 파장(fundamental wavelength)의 \(\tfrac12, \tfrac13, \tfrac14\), 등입니다. 첫 번째 이후의 급수의 모든 항은 이웃하는 항의 조화 평균(harmonic mean)입니다; 구문 조화 평균(harmonic mean)은 마찬가지로 음악으로부터 파생됩니다.
History
조화 급수가 발산한다는 사실은 니콜 오렘(Nicole Oresme)에 의해 14세기에 처음 입증되었지만, 이 성취는 어둠에 빠졌습니다. 증명은 17세기 피에트로 멩골리(Pietro Mengoli), 요한 베르누이(Johann Bernoulli), 및 야콥 베르누이(Jacob Bernoulli)에 의해 제공되었습니다.
역사적으로, 조화 수열은 건축가와 함께 특정 인기를 가져왔습니다. 이것은 바로크(Baroque) 시대에서, 건축가가 평면도(floor plans)와 입면도(elevations)의 비율(proportions)을 확립하고, 교회와 궁전의 내부와 외부 건축적인 세부 사항 사이의 조화 관계를 확립하기 위해 그들을 사용할 때, 특별나게 그러했습니다.
Divergence
조화 급수의 발산의 여러 가지 잘-알려진 증명이 있습니다. 그들의 몇 가지는 아래에 주어집니다.
Comparison test
발산을 증명하는 한 가지 방법은 조화 급수를 또 다른 발산 급수와 비교하는 것이며, 여기서 각 분모는 다음-가장-큰 이의 거듭제곱(power of two)으로 대체됩니다:
\(\quad\displaystyle \begin{align}
&{} 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + \frac{1}{6} + \frac{1}{7} + \frac{1}{8} + \frac{1}{9} + \cdots \\[12pt]
\ge {} &1 + \frac{1}{2} + \frac{1}{\color{red}{\mathbf{4}}} + \frac{1}{4} + \frac{1}{\color{red}{\mathbf{8}}} + \frac{1}{\color{red}{\mathbf{8}}} + \frac{1}{\color{red}{\mathbf{8}}} + \frac{1}{8} + \frac{1}{\color{red}{\mathbf{16}}} + \cdots
\end{align}\)
조화 급수의 각 항은 두 번째 급수의 대응하는 항보다 크거나 같고, 그러므로 조화 급수의 합은 두 번째 급수의 합보다 반드시 크거나 같습니다. 어쨌든, 두 번째 급수의 합은 무한대입니다:
\(\quad\displaystyle \begin{align}
&{} 1 + \left(\frac{1}{2}\right) + \left(\frac{1}{4}\!+\!\frac{1}{4}\right) + \left(\frac{1}{8}\!+\!\frac{1}{8}\!+\!\frac{1}{8}\!+\!\frac{1}{8}\right) + \left(\frac{1}{16}\!+\!\cdots\!+\!\frac{1}{16}\right) + \cdots \\[12pt]
={} &1 + \frac{1}{2} + \frac{1}{2} + \frac{1}{2} + \frac{1}{2} + \cdots = \infty
\end{align}\)
그것은 조화 급수의 합이 마찬가지로 반드시 무한대가 되는 것을 (비교 테스트(comparison test)에 의해) 따릅니다. 보다 정확하게, 위의 비교는 모든 각 양의(positive) 정수(integer) k에 대해 다음임을 입증합니다:
\(\quad\displaystyle \sum_{n=1}^{2^k} \frac{1}{n} \geq 1 + \frac{k}{2}\).
1350년경에 니콜 오렘(Nicole Oresme)에 의해 제안된, 증명은 중세 수학(medieval mathematics)의 중대한 점으로 수학 공동체에서 많은 사람들에 의해 고려됩니다. 그것은 오늘날 수학 수업에서 가르치는 여전히 표준 증명입니다. 코시의 응집 테스트(Cauchy's condensation test)는 이 논증의 일반화입니다.
Integral test
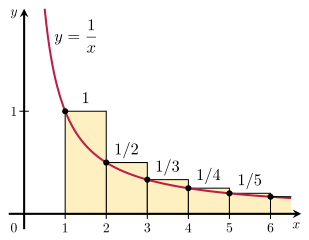
조화 급수는 그의 합을 부적절한 적분(improper integral)과 비교함으로써 발산하는 것을 증명할 수 있습니다. 특히, 오른쪽에 그림에서 보이는 사각형의 배열을 생각해 보십시오. 각 사각형은 1 단위 너비 및 \(\tfrac{1}{n}\) 단위 높이이므로, 무한한 숫자의 사각형의 전체 넓이는 조화 급수의 합입니다:
\(\quad\displaystyle \begin{array}{c} \text{area of} \\ \text{rectangles} \end{array}
= 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + \cdots\)
게다가, 1에서 무한대까지 곡선 \(y=\tfrac{1}{x}\) 아래의 전체 넓이는 발산하는 부적절한 적분(improper integral)에 의해 제공됩니다:
\(\quad\displaystyle \begin{array}{c} \text{area under} \\ \text{curve}\end{array}
= \int_1^\infty\frac{1}{x}\,dx = \infty.\)
이 넓이는 사각형 안에 완전히 포함되므로, 사각형의 전체 넓이는 마찬가지로 반드시 무한대입니다. 보다 정확하게, 이것은 다음임을 입증합니다:
\(\quad\displaystyle \sum_{n=1}^k \frac{1}{n} > \int_1^{k+1} \frac{1}{x}\,dx = \ln(k+1). \)
이 논증의 일반화는 적분 테스트(integral test)로 알려져 있습니다.
Rate of divergence
조화 급수는 매우 천천히 발산합니다. 예를 들어, 처음 \(10^{43}\) 항의 합은 100보다 작습니다. 이것은 급수의 부분 합이 로그 성장(logarithmic growth)을 가지기 때문입니다. 특히,
\(\quad\displaystyle \sum_{n=1}^k\frac{1}{n} = \ln k + \gamma + \varepsilon_k \leq (\ln k) + 1\)
여기서 \(\gamma\)는 오일러–마스케로니 상수(Euler–Mascheroni constant)이고 \(\varepsilon_k \sim \tfrac{1}{2k}\)는, k가 무한대로 갈 때, 0으로 접근합니다. 레온하르트 오일러(Leonhard Euler)는 이것과 단지 소수의 역수를 포함하는 합이 역시 발산한다는, 즉,
\(\quad\displaystyle \sum_{p\text{ prime }}\frac1p = \frac12 + \frac13 + \frac15 + \frac17 + \frac1{11} + \frac1{13} + \frac1{17} +\cdots = \infty\)
이라는 보다 놀라운 사실 둘 다를 입증했습니다.
Partial sums
발산하는 조화 급수의 유한 부분 합,
\(\quad\displaystyle H_n = \sum_{k = 1}^n \frac{1}{k},\)
은 조화 숫자(harmonic number)라고 불립니다.
\(H_n\)과 ln n 사이의 차이는 오일러–마스케로니 상수(Euler–Mascheroni constant)에 수렴합니다. 임의의 두 조화 숫자 사이의 차이는 결코 정수가 아닙니다. \(H_1=1\)을 제외한, 조화 숫자는 정수가 아닙니다.
Related series
Alternating harmonic series
급수
\(\quad\displaystyle \sum_{n = 1}^\infty \frac{(-1)^{n + 1}}{n} = 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \frac{1}{5} - \cdots\)
은 교대 조화 급수(alternating harmonic series)로 알려져 있습니다. 이 급수는 교대 급수 테스트(alternating series test)에 의해 수렴합니다. 특히, 합은 2의 자연 로그(natural logarithm of 2)와 같습니다:
\(\quad\displaystyle 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \frac{1}{5} - \cdots = \ln 2.\)
교대 조화 급수는, 조건적으로 수렴(conditionally convergent)하지만, 절대적으로 수렴(absolutely convergent)하지는 않습니다: 만약 급수에서 항이 체계적으로 재정렬되면, 일반적으로 합은 다르게 되고, 재정렬에 따라, 아마도 심지어 무한대도 됩니다.
교대 조화 급수 공식은 메르카토르 급수(Mercator series), 자연 로그에 대해 테일러 급수(Taylor series)의 특별한 경우입니다.
관련된 급수는 아크탄젠트(arctangent)에 대해 테일러 급수로부터 유도될 수 있습니다:
\(\quad\displaystyle \sum_{n = 0}^\infty \frac{(-1)^{n}}{2n+1} = 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \cdots = \frac{\pi}{4}.\)
이것은 라이프니츠 급수(Leibniz series)로 알려져 있습니다.
General harmonic series
일반적인 조화 급수(general harmonic series)는 다음 형식입니다:
\(\quad\displaystyle \sum_{n=0}^{\infty}\frac{1}{an+b} ,\)
여기서 a ≠ 0이고 b는 실수이고 \(\tfrac{b}{a}\)는 영이 아니거나 음의 정수입니다.
조화 급수와 함께 극한 비교 테스트에 의해, 모든 일반적인 조화 급수는 역시 발산합니다.
p-series
조화 급수의 일반화는 p-급수(p-series) (또는 초조화 급수(hyperharmonic series))이며, 임의의 양의 실수 p에 대해, 다음으로 정의됩니다:
\(\quad\displaystyle \sum_{n=1}^{\infty}\frac{1}{n^p}\).
p = 1일 때, p-급수는 조화 급수이며, 이것은 발산합니다. 적분 테스트 또는 코시 응집 테스트(Cauchy condensation test) 중 하나는, 모든 p > 1에 대해 p-급수는 수렴하고 (이 경우에서 그것은 위에-조화 급수(over-harmonic series)라고 불립니다) 모든 p ≤ 1에 대해 발산함을 보입니다. 만약 p > 1이면 p-급수의 합은 ζ(p), 즉, p에서 평가된 리만 제타 함수(Riemann zeta function)입니다.
p = 2에 대해 합을 찾는 문제는 바젤 문제(Basel problem)로 불립니다; 레온하르트 오일러는 그것이 \(\tfrac{\pi^2}{6}\)임을 보였습니다. p = 3에 대해 합의 값은 아페리 상수(Apéry's constant)로 불리는데, 왜냐하면 로저 아페리(Roger Apéry)가 그것이 무리수(irrational number)임을 입증했기 때문입니다.
ln-series
p-급수(p-series)와 관련된 ln-급수(ln-series)는, 임의의 양의 실수 p에 대해, 다음으로 정의됩니다:
\(\quad\displaystyle \sum_{n=2}^{\infty}\frac{1}{n (\ln n)^p}\;\).
이것은 p ≤ 1에 대해 발산하지만, 모든 p > 1에 대해 수렴하는 것이 적분 테스트에 의해 보일 수 있습니다.
φ-series
다음을 만족하는 임의의 볼록(convex), 실수-값 함수 φ에 대해
\(\quad\displaystyle \limsup_{u\to 0^+}\frac{\varphi(u/2)}{\varphi(u)} < \frac{1}{2}, \)
급수
\(\quad\displaystyle \sum_{n=1}^\infty \varphi\left(\frac{1}{n}\right)\)
는 수렴합니다.
Random harmonic series
\(s_n\)은 같은 확률 \(\tfrac12\)과 함께 값 +1과 −1을 취하는 독립적(independent), 동일하게 분포된 확률 변수인, 확률 조화 급수
\(\quad\displaystyle \sum_{n=1}^{\infty}\frac{s_{n}}{n},\)
는 확률 1로 수렴하는 확률 변수의 급수에 대해 확률 이론에서 잘 알려진 예제입니다. 이 수렴의 사실은 콜모고로프 삼-급수 정리(Kolmogorov three-series theorem) 또는 밀접하게 관련된 콜모고로프 최대 부등식(Kolmogorov maximal inequality) 둘 중의 하나의 쉬운 수렴입니다. 앨버타 대학의 바이런 슈무런드(Byron Schmuland)는 확률 조화 급수의 속성을 더 조사했고, 수렴하는 급수는 일부 흥미로운 속성을 갖는 확률 변수(random variable)임을 보였습니다. 특히, +2 또는 −2에서 평가된 이 확률 변수의 확률 밀도 함수(probability density function)는 값 0.124999999999999999999999999999999999999999764…을 가지며, \(\tfrac18\)에서 \(10^{-42}\)보다 작은 만큼 다릅니다. 슈무런드의 논문은 왜 이 확률이, 정확하지는 않지만, \(\tfrac18\)에 매우 가까운지를 설명합니다. 이 확률의 정확한 값은 무한 코사인 곱 적분 \(C_2\)을 π로 나눔으로써 제공됩니다.
Depleted harmonic series
분모가 제거된 어디에서나 자릿수 9가 나타나는 모든 항이 비워진 조화 급수는 수렴하는 것으로 보일 수 있고 그 값은 80보다 작습니다. 사실, (임의의 밑수에서) 자릿수의 임의의 특정 문자열을 포함하는 모든 항이 제거될 때, 급수는 수렴합니다.
Applications
조화 급수는 그것을 처음으로 마주한 학생들에게 반-직관적일 수 있는데, 왜냐하면 그것은 비록 n이 무한대로 갈 때 n번째 항의 극한이 영일지라도, 발산 급수(divergent series)이기 때문입니다. 조화 급수의 발산은 일부 명백한 역설(paradox)의 역시 원천입니다. 이것들의 한 예제가 "고무 밴드 위의 벌레"입니다. 고무 밴드가 균일하게 늘어날 때, 동시에 무한하게-늘어나는 일-미터 고무 밴드를 따라 벌레가 기어가는 것을 가정해 보십시오. 만약 벌레가 분당 1 센티미터 이동하고 밴드가 분당 1 미터 늘어나면, 벌레가 언젠가 고무 밴드의 끝에 도달할 수 있을까요? 대답은, 반-직관적으로, "예"이고, n분 후에 대해, 고무 밴드의 전체 길이에 대해 벌레에 의한 이동한 거리의 비율은 다음입니다:
\(\quad\displaystyle \frac{1}{100}\sum_{k=1}^n\frac{1}{k}.\)
(사실 실제 비율은, 밴드가 연속적으로 늘어날 때, 이 합보다 조금 작습니다.)
급수는, n이 커져감에 따라, 임의로 더 커지기 때문에, 결국 이 비율은 반드시 1을 초과하며, 이것은 벌레가 고무 밴드의 끝에 도달함을 의미합니다. 어쨌든, 이 발생에서 n의 값은 반드시 극단적으로 커야 합니다: 약 \(e^{100}\), \(10^{43}\) 분을 초과하는 숫자 (\(10^{37}\)년). 비록 조화 급수가 발산할지라도, 그것은 아주 천천히 행해집니다.
조화 급수를 포함하는 또 다른 문제는 지프 문제(Jeep problem)이며, 이것은 (하나의 형식에서) 사막을 가로-지르는 제한된 연료-운반 능력과 함께 지프(jeep)에 필요한 총 연료량을 묻는 것으로, 경로를 따라 연료를 흘릴 가능성은 고려하지 않습니다. 주어진 양의 연료로 이송할 수 있는 거리는 조화 급수의 부분 합과 관련되며, 이것은 로그적으로 증가합니다. 그래서 필요한 연료는 원하는 거리와 함께 지수적으로 증가합니다.
또 다른 예제는 블록-쌓기 문제(block-stacking problem)입니다: 동일한 도미노의 모음이 주어지면, 블록이 떨어지는 일없이 테이블의 가장자리에 매달려 있도록, 테이블의 가장자리에 그들을 쌓는 것이 분명히 가능합니다. 반-직관적인 결과는, 우리는, 충분한 도미노가 제공되면, 임의의 큰 돌출을 만들기 위해 그런 방법으로 블록을 쌓을 수 있다는 것입니다.
더 간단한 예제는, 다른 한편으로, 수영장의 벽을 터치할 때 보다 속도를 더하는 것을 유지하는 헤엄치는 사람입니다. 헤엄치는 사람은 2 m/s의 속력으로 10-미터 수영장을 횡단하기 시작하고, 모든 각 횡단과 함께, 또 다른 2 m/s가 속력에 더해집니다. 이론상으로, 헤엄치는 사람의 속력은 무제한이지만, 해당 속도를 얻기 위해 필요한 수영장 횡단의 횟수는 매우 커지게 됩니다; 예를 들어, (특수 상대성(special relativity)을 무시하는) 빛의 속력(speed of light)을 얻기 위해, 헤엄치는 사람은 수영장을 1억 5천만 번 횡단하는 것이 필요합니다. 이 큰 숫자와는 반대로, 주어진 속력에 도달하기 위해 필요한 시간은 (반복) 수영장 횡단의 임의의 주어진 숫자에서 급수의 합에 따라 다릅니다:
\(\quad\displaystyle \frac{10}{2}\sum_{k=1}^n\frac{1}{k}.\)
(반복적으로) 합을 계산하면 빛의 속력에 도달하기 위해 필요한 시간은 단지 94 초임을 보입니다. (빛의 속력을 초과하는, 다시 특수 상대성을 무시하는) 이 점을 뒤로 계속함으로써, 수영장을 횡단하는 데 걸리는 시간은, 반복의 숫자가 매우 커짐에 따라, 사실 영에 접근할 것이고, 비록 수영장을 횡단하기 위해 요구된 시간은 (무한대의 반복 횟수에서) 영으로 가는 경향이 있을지라도, (전체 수영장 횡단에 대해 걸린 시간) 반복의 합은 매우 느린 비율로 여전히 발산할 것입니다.
External links
- "Harmonic series", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- "The Harmonic Series Diverges Again and Again" (PDF). The AMATYC Review. 27: 31–43. 2006.
- Weisstein, Eric W. "Harmonic Series". MathWorld.
- Weisstein, Eric W. "Book Stacking Problem". MathWorld.
- Hudelson, Matt (1 October 2010). "Proof Without Words: The Alternating Harmonic Series Sums to ln 2" (PDF). Mathematics Magazine. 83 (4): 294. doi:10.4169/002557010X521831.