수학(mathematics)에서, 연속 함수(continuous function)는, 불연속(discontinuities)으로 알려진, 값에서 임의의 급격한 변화를 가지지 않는 함수(function)입니다. 보다 정확하게, 연속 함수의 입력에서 충분히 작은 변화는 그의 출력에서 임의의 작은 변화를 결과로서 가져옵니다. 그렇지 않으면, 함수는 불연속(discontinuous) 함수라고 말합니다. 연속 역함수(inverse function)를 갖는 연속 함수는 위상-동형(homeomorphism)으로 불립니다.
함수의 연속성은 토폴로지(topology)의 핵심 개념 중 하나이며, 토폴로지은 아래에서 전반적으로 다루어집니다. 이 기사의 도입 부분은 함수의 입력과 출력이 실수인 특별한 경우에 중점을 둡니다. 연속성의 더 강한 형식은 균등 연속성(uniform continuity)입니다. 게다가, 이 기사는 두 메트릭 공간(metric space) 사이에서 함수의 보다 일반적인 경우에 대한 정의를 토론합니다. 순서 이론(order theory), 특히 도메인 이론(domain theory)에서, 우리는 스콧 연속성(Scott continuity)으로 알려진 연속성의 개념을 고려합니다. 연속성의 다른 형식은 존재하지만 그들은 이 기사에서 토론되지 않습니다.
예제로써, 시간 t에서 자라는 꽃의 높이(height)를 나타내는, 함수 h(t)를 생각해 보십시오. 이 함수는 연속입니다. 대조적으로, 만약 M(t)가 시간 t에서 은행 계좌의 총 금액을 나타내면, 그 함수는 돈이 입금되거나 인출될 때 시간 안의 그러한 각 점에서 뛰어오르므로, 함수 M(t)는 불연속입니다.
History
연속성에 대한 엡실론–델타 정의(epsilon–delta definition)의 형식은 1817년에 베르나르트 볼차노(Bernard Bolzano)에 의해 처음으로 제공되었습니다. 오귀스탱-루이 코시(Augustin-Louis Cauchy)는 \(y=f(x)\)의 연속성을 다음으로 정의했습니다: 독립 변수 x의 무한히 작은 증분 \(\alpha\)는 종속 변수 y의 무한히 작은 변화 \(f(x+\alpha)-f(x)\)를 항상 생성합니다 (예를 들어, Cours d'Analyse, p. 34를 참조하십시요). 코시(Cauchy)는 변수 양의 관점에서 무한히 적은 양을 정의했고, 그의 연속성의 정의는 오늘날 사용되는 무한소 정의와 매우 유사합니다 (마이크로-연속성(microcontinuity)을 참조하십시요). 점마다 연속성(pointwise continuity)과 균등 연속성(uniform continuity) 사이의 공식적인 정의와 구별은 1830년대 볼차노에 의해 처음으로 제공되었지만 그 연구는 1930년대까지 출판되지 않았습니다. 볼차노처럼, 카를 바이어슈트라스(Karl Weierstrass)는, 만약 연속성이 c의 양측과 c에서 정의되지 않았다면ㅡ 점 c에서 함수의 연속성을 거부했지만, 에두아르 구르사(Édouard Goursat)는 함수가 오직 c의 한측과 c에서 정의되는 것을 허용했고, 카미유 조르당(Camille Jordan)은 심지어 함수가 오직 c에서 정의될지라도 그것을 허용했습니다. 점마다 연속성의 그들 비동등한 정의의 세 가지 모두는 여전히 사용 중입니다. 에두아르트 하이네(Eduard Heine)은 1872년에 균등 연속성의 첫번째 출판된 정의를 제공했지만, 1854년 페터 구스타프 르죈 디리클레(Peter Gustav Lejeune Dirichlet)에 의해 제공된 강의에 이들 아이디어의 기초를 두었습니다.
Real functions
Definition

실수 함수(real function), 즉 실수(real number)에서 실수로의 함수(function)는 데카르트 평면(Cartesian plane)에서 그래프(graph)에 의해 표현될 수 있습니다; 그러한 함수는 만약, 대략 말해서, 그래프가 그의 도메인(domain)이 전체 실수 직선에서 하나의 비-부러진 곡선(curve)이면, 연속입니다. 보다 수학적으로 엄격한 정의는 아래에 나와 있습니다.
실수 함수의 연속성의 엄격한 정의는 보통 극한(limit)의 개념의 관점에서 미적분학의 첫 번째 과정에서 주어집니다. 첫째, 변수 x를 갖는 함수 f는 만약 x가 그 점 c에 접근할 때, f(x)의 극한이 값 f(c)와 같으면, 실수 직선의 점 c에서 연속이라고 말합니다; 그리고 둘째, 만약 함수가 모든 각 점에서 연속이면, (전체적으로) 함수가 연속이라고 말합니다. 함수는, 그것이 그곳에서 연속이 아닐 때, 어떤 점에서 불연속(discontinuous) (또는 불연속성(discontinuity)을 가지는 것)이라고 말합니다. 이들 점들 자체는 역시 불연속성들(discontinuities)로 취급됩니다.
함수의 연속성의 여러-가지 다른 정의가 있습니다. 때때로 함수는, 만약 그것이 그의 도메인의 모든 각 점에서 연속이면, 연속이라고 말합니다. 이 경우에서, 모든 실수 x ≠ (2n+1)π/2, n 임의의 정수의 도메인을 갖는, 함수 f(x) = tan(x)는 연속입니다. 때때로 예외는 도메인의 경계에 대해 만들어집니다. 예를 들어, 모든 비-음의 실수의 도메인을 갖는, 함수 \(f(x)=\sqrt{x}\)의 그래프는 왼-쪽 끝점을 가집니다. 이 경우에서, 오직 오른쪽으로부터 극한이 함수의 값과 같아지는 것이 요구됩니다. 이 정의 아래에서, 함수 f는 경계 x = 0에서 연속이고 그래서 모든 비-음수 인수에 대해 마찬가지입니다. 가장 공통적이고 제한적인 정의는, 만약 함수가 모든 실수에서 연속이면, 함수가 연속이라는 것입니다. 이 경우에서, 앞의 두 예제는 연속이 아니지만, 모든 각 다항(polynomial) 함수는 연속이고, 사인(sine), 코사인(cosine), 및 지수 함수(exponential functions)도 마찬가지입니다. 단어의 의미가 의도되는 문맥에서 명확해 지도록, 단어 연속을 사용함에 있어 주의를 기울여야 합니다.
수학 표기법을 사용하여, 위에서 언급된 세 가지 의미의 각각에서 연속 함수를 정의하기 위해 여러-가지 방법이 있습니다.
다음을 놓습니다:
- \(f\colon D \rightarrow \mathbf R \quad\)를 실수의 집합 \(\mathbf R\)의 부분-집합(subset) \( D \) 위에 정의된 함수로 놓습니다.
이 부분 집합 \( D \)는 f의 도메인(domain)입니다. 어떤 가능한 선택은 다음을 포함합니다:
- \(D = \mathbf R \quad \) (\( D \)는 실수의 전체 집합입니다), 또는, a와 b 실수에 대해,
- \(D = [a, b] = \{x \in \mathbf R \,|\, a \leq x \leq b \} \quad \) (\( D \)는 닫힌 구간(closed interval)입니다), 또는
- \(D = (a, b) = \{x \in \mathbf R \,|\, a < x < b \} \quad \) (\( D \)는 열린 구간(open interval)입니다).
도메인 \(D\)가 열린 구간으로 정의되는 경우에서, \(a\)와 \(b\)는 위의 의미에서 경계가 아니고, \(f(a)\)와 \(f(b)\)의 값은 \(D\) 위에 연속성에 대해 문제되지 않습니다.
Definition in terms of limits of functions
함수 f는, 만약 f(x)의 극한(limit)이, f의 도메인을 통해 x가 c에 접근할 때, 존재하고 f(c)와 같으면, 그의 도메인의 어떤 점 c에서 연속입니다. 수학 표기법에서, 이것은 다음과 같이 쓰여집니다:
\(\quad\)\(\displaystyle \lim_{x \to c}{f(x)} = f(c).\)
자세하게, 이것은 다음 세 조건을 의미합니다: 첫째, f는 (c가 f의 도메인 안에 있어야 하는 요구-조건에 의해 보장되는) c에서 정의되어야 합니다. 둘째, 그 방정식의 왼쪽 변에 있는 극한이 존재해야 합니다. 셋째, 이 극한의 값은 반드시 f(c)와 같아야 합니다.
(우리는 여기서 f의 도메인은 임의의 고립된 점(isolated point:고립점)을 가지지 않는다고 가정합니다. 예를 들어, 구간 또는 구간의 합집합은 고립된 점을 가지지 않습니다.)
Definition in terms of neighborhoods
점 c의 이웃(neighborhood)은 c의 어떤 고정된 거리 안에 있는 ,적어도, 모든 점을 포함하는 집합입니다. 직관적으로, 함수는, 만약 c의 이웃에 걸쳐 f의 치역이 c를 중심으로 하는 이웃의 폭이 영으로 줄어들 때 하나의 점 f(c)로 줄어들면, 점 c에서 연속입니다. 보다 정확하게, 함수 f는, 만약, 임의의 이웃 \(N_1(f(c))\)에 대해 \(x\in N_2(c)\)일 때마다 \(f(x)\in N_1(f(c))\)를 만족하는 그의 도메인 안의 이웃 \(N_2(c)\)가 있으면, 그의 도메인 안의 점 c에서 연속입니다.
이 정의는 도메인과 코도메인이 토폴로지적 공간임을 단지 요구하고 따라서 가장 일반적인 정의입니다. 그것은, 함수 f는 그의 도메인의 모든 각 고립된 점(isolated point)에서 자동으로 연속이라는 이 정의로부터 따릅니다. 특정 예제로서, 정수 집합 위에 모든 각 실수-값 함수는 연속입니다.
Definition in terms of limits of sequences

우리는, c에 수렴(converges)하는 도메인 안의 점의 임의의 수열(sequence) \((x_n)_{n\in\mathbb{N}}\)에 대해, 해당하는 수열 \(\left(f(x_n)\right)_{n\in \mathbb{N}}\)은 f(c)로 수렴한다는 것을 대신 요구할 수 있습니다. 수학 표기법에서,
\(\quad\)\(\displaystyle \forall (x_n)_{n\in\mathbb{N}} \subset D:\lim_{n\to\infty} x_n=c \Rightarrow \lim_{n\to\infty} f(x_n)=f(c)\,.\)
Weierstrass and Jordan definitions (epsilon–delta) of continuous functions

함수의 극한의 정의를 명시적으로 포함하여, 우리는 자체-포함된 정의를 얻습니다: 위에서 처럼 함수 f : D → R와 도메인 D의 원소 \(x_0\)가 주어지면, f는 따라오는 내용을 유지할 때, 점 \(x_0\)에서 연속이라고 말합니다: 임의의 숫자 ε > 0, 어쨌든 작은 것에 대해, \(x_0-\delta < x < x_0+\delta\)와 함께 f의 도메인 안에 모든 x에 대해, f(x)의 값이 다음을 만족시키는 어떤 숫자 δ > 0가 존재합니다:
\(\quad\)\( f(x_0) - \varepsilon < f(x) < f(x_0) + \varepsilon.\)
대안적으로 쓰여지는, \(x_0 \in D\)에서 f : D → R의 연속성은, 모든 ε > 0에 대해, 모든 x ∈ D 에 대해 다음을 만족시키는 δ > 0가 존재하는 것을 의미합니다:
\(\quad\)\(| x - x_0 | < \delta \Rightarrow | f(x) - f(x_0) | < \varepsilon. \)
보다 직관적으로, 우리는, 만약 우리가 \(f(x_0)\) 주변의 어떤 작은 이웃(neighborhood) 안에 모든 f(x) 값을 얻기를 원한다면, 우리는 \(x_0\) 주위의 x 값에 대해 충분히 작은 이웃을 선택하는 것이 단순히 필요하다고 말할 수 있습니다. 만약 우리가 f(x) 이웃이 아무리 작더라도 그것을 수행할 수 있으면, f는 \(x_0\)에서 연속입니다.
현대 용어에서, 이것은 토폴로지에 대해 기저(basis), 여기서 메트릭 토폴로지(metric topology)에 관한 함수의 연속성의 정의에 의해 일반화됩니다.
바이어슈트라스는 구간 \(x_0-\delta < x < x_0+\delta\)를 도메인 D 안에 전적으로 있어야 한다고 요구했었지만, 조르당은 그 제한을 제거했습니다.
Definition in terms of control of the remainder
증명과 수치 해석학에서, 우리는 종종 얼마나 빨리 극한이 수렴하는지, 또는 다른 말로, 나머지의 제어를 하는지를 아는 것이 필요합니다. 우리는 이것을 연속성의 정의로 공식화할 수 있습니다. 함수 \(C: [0,\infty) \to [0,\infty]\)는 만약 다음이면, 제어 함수라고 불립니다:
- C는 비-감소하는 것입니다
- \( \inf_{\delta > 0} C(\delta) = 0\)
함수 f : D → R는, 만약 다음이면, \(x_0\)에서 C-연속입니다:
\(\quad\)모든 \( x \in D \)에 대해 \(| f(x) - f(x_0)| \le C(|x- x_0|)\)입니다.
함수는, 만약 그것이 어떤 제어 함수 C에 대해 C-연속이면, \(x_0\) 안에 연속입니다.
이 접근법은 허용-가능한 제어 함수의 집합을 제한하는 것에 의해 연속성의 개념을 자연스럽게 정제하는 것으로 이어집니다. 제어 함수 \(\mathcal{C}\)의 주어진 집합에 대해, 함수는, 만약 그것이 어떤 \( C \in \mathcal{C}\)에 대해 \(C\)-연속이면, \(\mathcal{C}\)-연속입니다. 예를 들어 아래의 지수 \(\alpha\)의 립시츠(Lipschitz) 및 횔더 연속 함수(Hölder continuous function)는 다음 제어 함수의 집합에 의해 정의됩니다:
\(\quad\)\(\mathcal{C}_{\mathrm{Lipschitz}} = \{C | C(\delta) = K|\delta| ,\ K > 0\} \)
각각
\(\quad\)\(\mathcal{C}_{\text{Hölder}-\alpha} =\)\( \{C | C(\delta) = K |\delta|^\alpha, \ K > 0\} \).
Definition using oscillation

연속성은 진동의 관점에서 역시 정의될 수 있습니다: 함수 f는 점 \(x_0\)에서 연속인 것과 해당 점에서 그의 진동이 영인 것은 필요충분 조건입니다; 기호에서, \(\omega_f(x_0) = 0.\) 이 정의의 이점은 그것이 불연속성을 정량화한다는 것입니다: 진동은 그 점에서 함수가 얼마나 많이 불연속적인지를 제공합니다.
이 정의는 불연속성 및 연속 점의 집합을 연구하기 위해 기술적 집합 이론(descriptive set theory)에서 유용합니다 – 연속 점은 진동이 ε보다 작은 집합의 교집합입니다 (그러므로 \(G_{\delta}\) 집합) – 그리고 르베그 적분-가능성 조건(Lebesgue integrability condition)의 한 방향의 매우 빠른 증명을 제공합니다.
진동은 단순한 재-배치, 및 진동을 정의하기 위해 극한 (lim sup, lim inf)을 사용함으로써 ε-δ 정의와 동등합니다: 만약 (주어진 점에서) 주어진 \(\epsilon_0\)에 대해 ε-δ 정의를 만족시키는 δ가 없으면, 진동은 적어도 \(\epsilon_0\)이고, 반대로 만약 모든 각 ε에 대해 희망된 δ가 있으면, 진동은 0입니다. 진동 정의는 토폴로지적 공간에서 메트릭 공간으로 맵핑에 대해 자연스럽게 일반화될 수 있습니다.
Definition using the hyperreals
코시(Cauchy)는 다음의 직관적인 관점에서 함수의 연속성을 정의했습니다: 독립 변수에서 무한소(infinitesimal) 변화는 종속 변수의 무한소 변화에 해당합니다 (Cours d'analyse, 페이지 34를 참조하십시요). 비-표준 해석학(Non-standard analysis)은 이것을 수학적으로 엄격하게 만드는 방법입니다. 실수 직선은 초실수(hyperreal numbers)를 형성하기 위해 무한대 및 무한소 숫자의 추가에 의해 증대됩니다. 비표준 해석학에서, 연속성은 다음으로 정의될 수 있습니다.
- 실수-값 함수 f는, 만약 초실수에 대한 그의 자연스러운 확장이 모든 무한소 dx에 대해, f(x+dx) − f(x)가 무한소인 속성을 가지면, x에서 연속입니다.
(마이크로-연속성을 참조하십시요). 다른 말로, 독립 변수의 무한소 증분은 종속 변수의 극한소 변화를 항상 생성하며, 연속성의 오귀스탱-루이 코시(Augustin-Louis Cauchy)의 정의에 대한 현대적인 표현을 제공합니다.
Construction of continuous functions
주어진 함수의 연속성을 검사하는 것은 주어진 함수의 빌딩 블록에 대해 위의 정의하는 속성 중 하나를 검사함으로써 단순화될 수 있습니다. 어떤 도메인 위에 연속인, 두 함수의 합은, 이 도메인 위에 역시 연속임을 보여주는 것은 간단합니다. 다음이 주어지면
\(\quad\)\(f, g\colon D \rightarrow \mathbf R\),
그런-다음 (모든 \(x\in D\)에 대해 \(s(x) = f(x) + g(x)\)에 의해 정의된) 연속 함수의 합
\(\quad\)\(s = f + g\)
은 \(D\)에서 연속입니다.
같은 것이 연속 함수의 곱에 대해 유지됩니다. (모든 \(x \in D\)에 대해 \(p(x) = f(x) \cdot g(x)\)에 의해 정의된)
\(\quad\)\(p = f \cdot g\)
는 \(D\)에서 연속입니다.
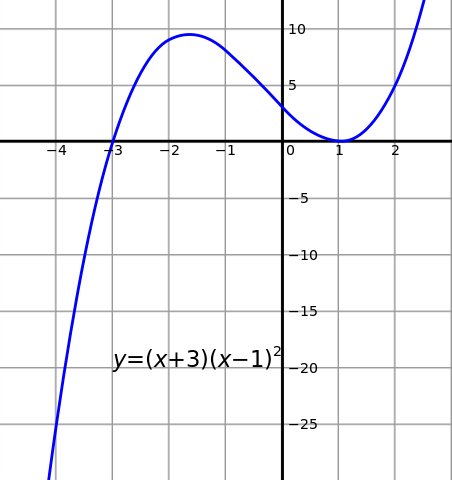
연속성의 위의 보존 및 상수 함수(constant function)의 연속성 및 \(\mathbf R\) 위의 항등 함수(identity function) \(I(x) = x\)의 연속성을 결합하여, 우리는 다음과 같은 \(\mathbf R\) 위의 모든 다항 함수(polynomial function)의 연속성에 도달합니다:
\(\quad\)\(f(x)=x^3+x^2-5x+3\)
(오른쪽 그림을 참조하십시요).
같은 방법에서, 그것은 다음 연속 함수의 역을 보여질 수 있습니다: (\(f(x) \ne 0\)를 만족하는 모든 \(x \in D\)에 대해 \(r(x) = 1/f(x)\)에 대해 정의된)
\(\quad\)\(r = 1/f\)
은 \(D\smallsetminus \{x:f(x) = 0\}\)에서 연속입니다.
이것은 \(g\)의 근을 제외하는 것을 의미하며, (\(g(x) \ne 0\)를 만족하는, 모든 \(x \in D\)에 대해 \(g(x) = f(x)/g(x)\)에 의해 정의된,) 다음 연속 함수의 몫
\(\quad\)\(q = f/g\)
은 D \(D\smallsetminus \{x:g(x) = 0\}\) 위에 연속입니다.
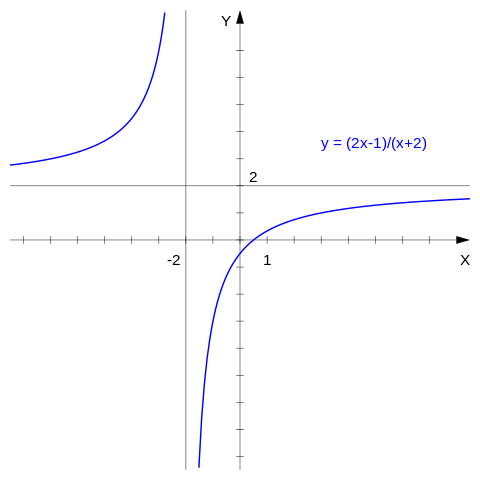
예를 들어, (오른쪽 그림의) 함수
\(\quad\)\(\displaystyle y(x) = \frac {2x-1} {x+2}\)
는 모든 실수 x ≠ −2에 대해 정의되고 모든 각 그런 점에서 연속입니다. 따라서 그것은 하나의 연속 함수입니다. x = −2에서 연속성의 질문은 발생하지 않는데, 왜냐하면 x = −2는 y의 도메인 안에 없습니다. 모든 x ≠ −2에 대해 y(x)에 일치하는 연속 함수 F: R → R는 없습니다.
함수 사인(sine)은 모든 실수 위에 연속이므로, 싱크 함수(sinc function) \(G(x)=\sin x / x\)는 정의되고 모든 실수 x ≠ 0에 대해 연속입니다. 어쨌든, 이전 예제와 달리, G는, 값 G(0)를, x가 0에 접근할 때, G(x)의 극한으로, 1이 되는 것, 즉, 다음과 같이 정의함으로써, 모든 실수 위에 연속 함수로 확장될 수 있습니다:
\(\quad\)\(\displaystyle G(0) = \lim_{x\rightarrow 0}\frac{\sin x}{x} = 1\)
따라서, 다음을 설정함으로써
\(\quad\)\(G(x) =
\begin{cases}
\frac {\sin (x)}x & \text{ if }x \ne 0\\
1 & \text{ if }x = 0,
\end{cases}\)
싱크-함수는 모든 실수 위에 연속 함수가 됩니다. 용어 제거-가능한 특이점(removable singularity)은, 적절한 극한과 일치하는 함수의 값을 (재)정의하는 것이 특정 점에서 함수를 연속으로 만들 때, 그러한 경우에서 사용됩니다.
연속 함수의 보다 포함된 구성은 함수 합성(function composition)입니다. 두 연속 함수가 주어지면
\(\quad\)\(f\colon D_f \;(\subseteq \mathbf R) \rightarrow R_f\; (\subseteq \mathbf R)\quad\) 및 \(\quad g\colon D_g\; (R_f \subseteq D_g) \rightarrow R_g \;(\subseteq \mathbf R),\)
그들의 합성은, \(c = g \circ f \colon D_f \rightarrow \mathbf R\)으로 나타내고, \(c(x) = g(f(x))\)에 의해 정의되면, 연속입니다.
이 구성은, 예를 들어, 다음과 같은 것을 말하는 것을 허용합니다:
\(\quad\)\(e^{\sin(\ln x)}\)는, 모든 \(x > 0\)에 대해, 연속입니다.
Examples of discontinuous functions
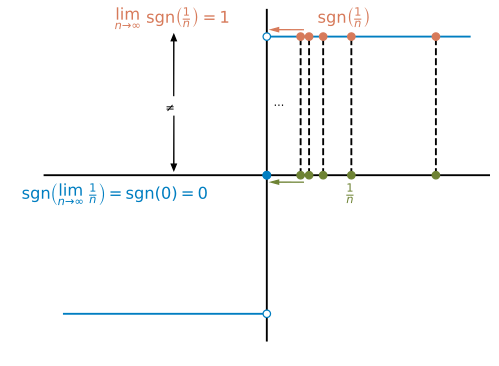
불연속 함수의 예제는 헤비사이드 계단 함수(Heaviside step function) \(H\)이며, 다음에 의해 정의됩니다:
\(\quad\)\(H(x) = \begin{cases}
1 & \text{ if } x \ge 0\\
0 & \text{ if } x < 0
\end{cases}
\)
예를 들어 \(\varepsilon = 1/2\)를 선택하십시오. 그러면 \(x = 0\) 주위에 \(\delta\)-이웃이 없습니다, 즉, \(\delta > 0\)을 가진 열린 구간 \((-\delta,\;\delta)\)이 없으며, 그것은 모든 \(H(x)\) 값을 \(H(0)\)의 \(\varepsilon\)-이웃 안에, 즉, \((1/2,\;3/2)\) 안에 강제할 것입니다. 직관적으로 우리는 함수 값에서 갑작스러운 점프(jump)와 같이 불연속성의 이 유형을 생각할 수 있습니다.
비슷하게, 부호 함수(signum 또는 sign function)
\(\quad\)\(\rm{sgn}(x) = \begin{cases}
\;\;\ 1 & \text{ if }x > 0\\
\;\;\ 0 & \text{ if }x = 0\\
-1 & \text{ if }x < 0
\end{cases}\)
은 \(x = 0\)에서 불연속이지만 다른 모든 곳에서 연속입니다. 또 다른 예제: 함수
\(\quad\)\(f(x)=\begin{cases}
\sin\left(x^{-2}\right)&\text{ if }x \ne 0\\
0&\text{ if }x = 0
\end{cases}\)
는 \(x = 0\)를 제외한 모든 곳에서 연속입니다.
위와 같은 그럴듯한 연속성과 불연속성 외에도, 종종 병리학적(pathological)으로 만들어 낸, 행동을 가진 함수가 역시 있으며, 예를 들어, 토메의 함수(Thomae's function),
\(\quad\)\(f(x)=\begin{cases}
1 &\text{ if }x=0\\
\frac{1}{q}&\text{ if }x=\frac{p}{q}\text{(in lowest terms) is a rational number}\\
0&\text{ if }x\text{ is irrational}.
\end{cases}\)
는 모든 무리수에서 연속이고 모든 유리수에서 불연속입니다. 비슷한 맥락에서, 디리클레의 함수(Dirichlet's function), 유리수의 집합에 대해 지시 함수(indicator function),
\(\quad\)\(D(x)=\begin{cases}
0&\text{ if }x\text{ is irrational } (\in \mathbb{R} \smallsetminus \mathbb{Q})\\
1&\text{ if }x\text{ is rational } (\in \mathbb{Q})
\end{cases}\)
는 연속인 곳이 없습니다.
Properties
Intermediate value theorem
사잇값 정리(intermediate value theorem)는, 완전성(completeness)의 실수 속성에 기초한, 존재 정리(existence theorem)이고, 다음을 말합니다:
- 만약 실수-값 함수 f가 닫힌 구간(closed interval) [a, b] 위에 연속이고 k가 f(a)와 f(b) 사이의 어떤 숫자이면, f(c) = k를 만족하는 [a, b] 안에 어떤 숫자 c가 있습니다.
예를 들어, 만약 한 어린이가 두 살과 여섯 살 사이에 1 m에서 1.5 m까지 자란다면, 두 살과 여섯 살 사이의 어느 시점에서, 그 어린이의 키는 반드시 1.25 m를 가졌을 것입니다.
결과적으로, 만약 f가 [a, b] 위에 연속이고 f(a)와 f(b)가 부호(sign)가 다르면, [a, b] 안의 어떤 점 c에서, f(c)는 반드시 영(zero)과 같습니다.
Extreme value theorem
극단 값 정리(extreme value theorem)는, 만약 하나의 함수 f가 닫힌 구간 [a,b] (또는 임의의 닫힌 그리고 경계진 집합) 위에 정의되고 그곳에서 연속이면, 그 함수는 그의 최댓값을 가집니다, 즉, 모든 x ∈ [a,b]에 대해 f(c) ≥ f(x)를 가진 c ∈ [a,b]가 존재합니다. 같은 것이 f의 최솟값에 대해 참입니다. 이 명제는, 만약 그 함수가 열린 구간 (a,b) (또는 닫힌 및 경계진 둘 다는 아닌 임의의 집합) 위에 정의되면, 일반적으로, 참이 아닙니다, 예를 들어, 열린 구간 (0,1) 위에 정의된, 연속 함수 f(x) = 1/x는, 위쪽 경계가 없으므로, 최댓값을 가지지 않습니다.
Relation to differentiability and integrability
모든 각 미분 가능한 함수(differentiable function)
\(\quad\)\(f\colon (a, b) \rightarrow \mathbf R\)
은, 보여왔던 것처럼, 연속입니다. 그 전환(converse)은 유지되지 않습니다: 예를 들어, 절댓값(absolute value) 함수
\(\quad\)\(f(x)=|x| = \begin{cases}
\;\;\ x & \text{ if }x \geq 0\\
-x & \text{ if }x < 0
\end{cases}\)
은 모든 곳에서 연속입니다. 어쨌든, 그것은 x = 0에서 미분 가능하지 않습니다 (그러나 이 곳을 제외하면 미분-가능입니다). 바이어슈트라스의 함수(Weierstrass's function)는 모든 곳에서 역시 연속이지만 미분-가능한 곳은 없습니다.
미분-가능한 함수 f(x)의 도함수(derivative) f′(x)는 연속일 필요는 없습니다. 만약 f′(x)가 연속이면, f(x)는 연속적으로 미분-가능하다고 말합니다. 그러한 함수의 집합은 \(C^1((ab))\)로 표시됩니다. 보다 일반적으로, 함수 f는 n 번 미분 가능하고 f의 n-번째 도함수는 연속을 만족하는, (열린 구간 (또는 R의 열린 부분 집합) Ω에서 실수로의) 다음 함수의 집합
\(\quad\)\(f\colon \Omega \rightarrow \mathbf R\)
은 \(C^n (\Omega)\)로 표시됩니다. 미분-가능성 클래스(differentiability class)를 참조하십시요. 컴퓨터 그래픽의 분야에서, \(C^0, C^1, C^2\)에 관련된 (그러나 일치하는 것은 아닌) 속성은 때때로 \(G^0\) (위치의 연속성), \(G^1\) (접선의 연속성), 및 \(G^2\) (곡률의 연속성)으로 불립니다; 곡선과 표면의 매끄러움(Smoothness of curves and surfaces)을 참조하십시오.
모든 각 연속 함수
\(\quad\)\(f\colon [a, b] \rightarrow \mathbf R\)
는 (예를 들어 리만 적분(Riemann integral)의 의미에서) 적분-가능(integrable)입니다. 그 역은 유지되지 않는데, 예를 들어, (적분-가능이지만, 불연속인) 부호 함수(sign function)가 보여줍니다.
Pointwise and uniform limits
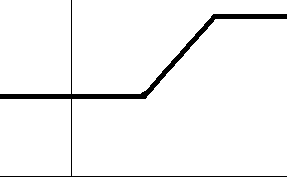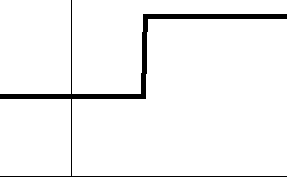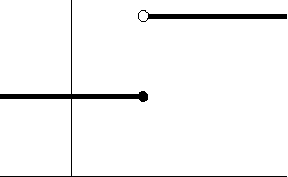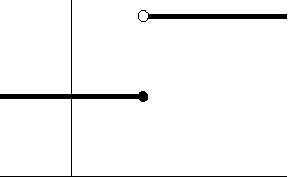
D의 모든 x에 대해 극한
\(\quad\)\(\displaystyle f(x) := \lim_{n \rightarrow \infty} f_n(x)\)
이 존재하는 것을 만족하는 함수의 수열(sequence)
\(\quad\)\(f_1, f_2, \dotsc \colon I \rightarrow \mathbf R\)
이 주어지면, 결과 함수 f(x)는 함수의 수열 \(f_n)_{n\in \mathbf{N}}\)의 점마다 극한(pointwise limit)으로 참조됩니다. 점마다 극한 함수는, 오른쪽에 보여지는 애미메이션처럼, 심지어 모든 함수 \(f_n\)이 연속일지라도, 연속일 필요는 없습니다. 어쨌든, f는, 만약 모든 함수 \(f_n\)이 연속이고 수열이, 균등 수렴 정리(uniform convergence theorem)에 의해, 균등하게 수렴(converges uniformly)하면, 연속입니다. 이 정리는 지수 함수(exponential function), 로그(logarithm), 제곱 근(square root) 함수, 및 삼각 함수(trigonometric function)가 연속임을 보여주기 위해 사용될 수 있습니다.
Directional and semi-continuity
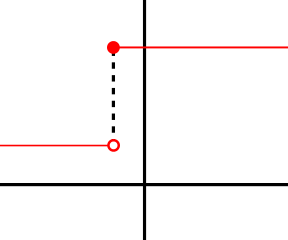
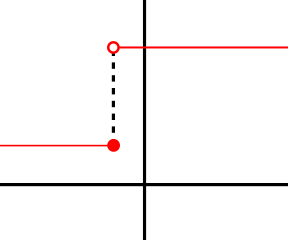
불연속 함수는 제한된 방식으로 불연속일 수 있으며, 방향성 연속성 (또는 왼쪽과 오른쪽 연속 함수) 및 반-연속성(semi-continuity)의 개념을 발생시킵니다. 대략 말하면, 함수는, 만약 극한 점이 오른쪽에서 접근될 때 점프가 발생하지 않으면, 오른쪽-연속입니다. 공식적으로, f는, 만약 다음이 유지되면, 점 c에서 오른쪽-연속이라고 말합니다: 임의의 숫자 ε > 0, 어쨌든 작은 것에 대해, c < x < c + δ을 가진 도메인 안의 모든 x에 대해, f(x)의 값이 다음을 만족시킬 수 있는, 어떤 숫자 δ > 0가 존재합니다:
\(\quad\)\( |f(x) - f(c)| < \varepsilon.\)
이것은 연속 함수에 대한 것처럼 같은 조건이지만, 그것은 x가 오직 c보다 엄격하게 큰 것에 대해 유지하기 위해 요구되는 것을 제외입니다. 대신 c − δ < x < c를 가진 모든 x에 대해 그것을 요구함으로써 왼쪽-연속 함수의 개념을 산출됩니다. 함수가 연속인 것과 그것이 오른쪽-연속 및 왼쪽-연속 둘 다인 것은 필요충분 조건입니다.
함수 f는, 만약, 대략, 임의의 점프가 오직 아래로 떨어지지만, 위로 올라가지 않으면, 아래로 반-연속(lower semi-continuous)입니다. 즉, 임의의 ε > 0에 대해, |x − c| < δ를 가진 도메인 안의 모든 x에 대해, f(x)의 값이 다음을 만족시키는, 어떤 숫자 δ > 0가 존재합니다:
\(\quad\)\(f(x) \geq f(c) - \epsilon.\)
역 조건은 위로 반-연속(upper semi-continuity)입니다.
Continuous functions between metric spaces
연속 실수-값 함수의 개념은 메트릭 공간(metric space) 사이의 함수로 일반화될 수 있습니다. 메트릭 공간은, X에 있는 임의의 두 원소의 거리의 측정으로 생각될 수 있는, 함수 (메트릭(metric)으로 불리우는) \(d_X\)를 갖춘 집합 X입니다. 공식적으로, 메트릭은, 많은 요구-사항, 특히 삼각형 부등식(triangle inequality)을 충족시키는 다음 함수입니다:
\(\quad\)\(d_X \colon X \times X \rightarrow \mathbf R\).
두 메트릭 공간 \((X,d_X)\)와 \((Y,d_Y)\) 및 다음 함수가 주어지면:
\(\quad\)\(f\colon X \rightarrow Y\),
f는 만약 임의의 양의 실수 ε에 대해, \(d_X(x,c) < \delta\)를 만족시키는 X 안의 모든 x가 \(d_Y(f(x),f(c)) < \varepsilon\)를 역시 만족시킬수 있는 양의 실수 δ가 존재한다면, (주어진 메트릭에 관해) X 안의 점 c에서 연속입니다. 위의 실수 함수의 경우에서 처럼, 이것은, 극한 \(\lim x_n = c\)을 가진 X 안의 모든 각 수열 \((x_n)\)에 대해, 우리는 \(\lim f(x_n)=f(c)\)를 가지는 조건과 동등합니다 후자의 조건은 다음으로 약화될 수 있습니다: f가 점 c에서 연속인 것과 극한 c를 가진 X 안의 모든 수렴하는 수열 \(\{x_n\}\)에 대해, 수열 \((f(x_n))\)이 코시 수열(Cauchy sequence)이고, c는 f의 도메인 안에 있는 것은 필요충분 조건입니다.
메트릭 공간 사이의 함수가 연속인 것에서 점의 집합은 \(G_{\delta}\) 집합입니다 – 이것은 연속성의 ε-δ 정의를 따릅니다.
연속성의 이 개념은, 예를 들어, 함수형 해석학(functional analysis)에서 적용됩니다. 이 분야에서 핵심 명제는 (||x||로 표시되는, 호환-가능한 노름(norm)을 갖춘 벡터 공간(vector spaces)인) 노름 벡터 공간(Normed vector spaces) V와 W 사이의 선형 연산자
\(\quad\)\(T\colon V \rightarrow W\)
가 연속인 것과 그것이 경계진(bounded), 즉, V 안의 모든 x에 대해 다음
\(\quad\)\(\|T(x)\| \leq K \|x\|\)
를 만족하는 상수 K가 있는 것은 필요충분 조건이라고 말합니다.
Uniform, Hölder and Lipschitz continuity
메트릭 공간 사이의 함수에 대한 연속성의 개념은 위의 정의에서 δ가 ε 및 c에 의존하는 그 방법을 제한함으로써 다양한 방법으로 강화될 수 있습니다. 직관적으로, 위에서 처럼 함수 f는, 만약 δ가 점 c에 의존하지 않으면, 균등 연속(uniformly continuous)입니다. 보다 정확하게, 그것이 모든 각 실수(real number) ε > 0에 대해, \(d_X(b,c) < \delta\)를 가진 모든 각 c, b ∈ X에 대해 만족하는 δ > 0가 존재하는 것이 요구되며, 우리는 \(d_Y(f(b),f(c)) < \varepsilon\)임을 가집니다. 따라서, 임의의 균등 연속 함수는 연속입니다. 역은 일반적으로 유지되지 않지만, 도메인 공간 X가 컴팩트(compact)일 때 유지됩니다. 균등 연속 맵핑은 균등 공간(uniform space)의 보다 일반적인 상황에서 정의될 수 있습니다.
함수는, 만약 X 안의 모든 b와 c에 대해, 부등식
\(\quad\)\(d_Y (f(b), f(c)) \leq K \cdot (d_X (b, c))^\alpha\)
을 유지하는 상수 K가 있으면, 지수 (하나의 실수) α와 함께 횔더 연속(Hölder continuous)입니다. 임의의 횔더 연속 함수는 균등적으로 연속입니다. 특별한 경우 α = 1은 립시츠 연속성(Lipschitz continuity)을 참조합니다. 즉, 함수는, 만약 X 안의 임의의 b, c에 대해, 부등식
\(\quad\)\(d_Y (f(b), f(c)) \leq K \cdot d_X (b, c)\)
이 유지되는 상수 K가 있으면, 립시츠 연속입니다. 립시츠 조건은, 예를 들어, 보통의 미분 방정식(ordinary differential equation)의 해에 관련하는 피카르-린델뢰프 정리(Picard–Lindelöf theorem)에서 발생합니다.
Continuous functions between topological spaces
또 다른, 보다 추상적인, 연속성의 개념은, 메트릭 공간(metric space)의 경우에서 있는 것처럼, 거리의 공식적인 개념이 일반적으로 없는 것에서, 토폴로지적 공간(topological space) 사이의 함수의 연속성입니다. 토폴로지적 공간은 X 위의 토폴로지와 함께 집합 X이며, 이것은 주어진 점의 이웃(neighbourhoods)에 대해서 얘기하는 것을 여전히 허용하는 동안 메트릭 공간에서 열린 공(open ball)의 속성을 일반화하는 그들의 합집합과 교집합에 관한 몇 가지 요구-사항을 만족시키는 X의 부분-집합(subset)의 집합입니다. 토폴로지의 원소는 X의 (포톨로지에 관한) 열린 부분-집합(open subset)으로 불립니다.
두 토폴로지적 공간 X와 Y 사이의 함수
\(\quad\)\(f\colon X \rightarrow Y\)
는, 만약 모든 각 열린 집합 V ⊆ Y에 대해, 역 이미지(inverse image)
\(\quad\)\(f^{-1}(V) = \{x \in X \; | \; f(x) \in V \}\)
가 X의 열린-부분 집합이면, 연속입니다. 즉, f는 (토폴로지 \(T_X\)의 원소가 아닌) 집합 X와 Y 사이의 함수이지만, f의 연속성은 X와 Y에서 사용되는 토포로지에 따라 달라집니다.
이것은 Y에서 (열린 부분-집합의 여집합인) 닫힌 집합(closed set)의 이전-이미지(preimages)가 X에서 닫혀진 것인 조건과 동등합니다.
극단적인 예제: 만약 집합 X가 (모든 각 부분-집합이 열려 있는) 이산 토폴로지(discrete topology)로 주어지면, 임의의 토폴로지적 공간 T에 대한 다음 모든 함수
\(\quad\)\(f\colon X \rightarrow T\)
는 연속입니다. 다른 한편으로, 만약 X가 (오직 열린 부분-집합이 빈 집합과 X인) 비-이산 토폴로지(indiscrete topology)를 갖추고 공간 T 집합이 적어도 \(T_0\)이면, 유일한 연속 함수는 상수 함수입니다. 반대로, 그의 치역이 비-이산인 임의의 함수는 연속입니다.
Continuity at a point
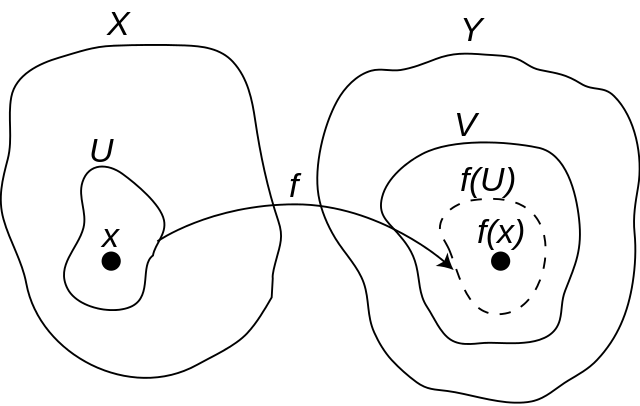
연속성의 (ε, δ)-정의((ε, δ)-definition of continuity)의 이웃의 언어에서 평행이동은 한 점에서 연속성의 다음 정의로 이어집니다:
- 함수 \(f:X\rightarrow Y\)가 점 \(x\in X\)에서 연속인 것과 Y 안의 \(f(x)\)의 임의의 이웃 V에 대해, f(U) ⊆ V를 만족하는 x의 이웃 U가 있는 것은 필요충분 조건입니다.
이 정의는 열린 이웃에 대한 제한된 이웃과 함께 같은 명제와 동등하고 이미지라기 보다는 이전-이미지(preimage)를 사용함으로써 여러 방법으로 다시-말할 수 있습니다.
또한, 이웃을 포함하는 모든 각 집합이 역시 이웃이고, \(f^{-1}(V)\)는 f(U) ⊆ V를 만족하는 X의 가장 큰 부분-집합 U일 때, 이 정의는 다음으로 단순화될 수 있습니다:
- 함수 \(f:X\rightarrow Y\)는 점 \(x\in X\)에서 연속인 것과 \(f^{-1}(V)\)가 Y 안의 \(f(x)\)의 모든 각 이웃 V에 대해 x의 이웃인 것은 필요충분 조건입니다.
열린 집합이 모든 그의 점의 이웃인 집합일 때, 함수 \(f:X\rightarrow Y\)가 X의 모든 각 점에서 연속인 것과 그것이 연속 함수인 것은 필요충분 조건입니다.
만약 X와 Y가 메트릭 공간이면, 그것이, 모든 이웃 대신에 f(x) 및 x를 중심으로 열린 공(open ball)의 이웃 시스템(neighborhood system)을 고려하는 것과 동등합니다. 이것은 메트릭 공간의 문맥에서 연속성의 위의 δ-ε 정의를 되돌려 줍니다. 일반적인 토폴로지적 공간에서, 근처 또는 거리에 대한 개념이 없습니다. 만약 어쨌든 목표 공간이 하우스도르프 공간(Hausdorff space)이면, f가 a에서 연속인 것과 x가 a로 접근할 때 f의 극한은 f(a)인 것은 필요충분 조건이라는 것은 여전히 참입니다. 고립된 점에서, 모든 각 함수는 연속입니다.
Alternative definitions
토폴로지 구조에 대한 여러 동등한 정의가 존재하고 따라서 연속 함수를 정의하기 위한 여러 동등한 방법이 있습니다.
Sequences and nets
여러 문맥에서, 공간의 토폴로지는 극한 점(limit points)의 관점에서 편리하게 지정됩니다. 많은 예제에서, 이것은, 점이 수열의 극한(limit of a sequence)일 때, 지정함으로써 달성되어지만, 어떤 의미에서 너무 큰 일부 공간에 대해, 우리는, 하나의 점이, 네트(nets)로 알려진, 방향화 집합(directed set)에 의해 인덱스된 점의 보다 일반적인 집합의 극한일 때, 역시 지정합니다. 함수가 오직 그것이 수열의 극한에서 수열의 극한을 취하면 (하이네-)연속입니다. 전자의 경우에서, 극한의 보존은 역시 충분입니다; 후자에서, 함수는 모든 수열의 극한을 보존할 수 있지만 그럼에도 불구하고 여전히 연속인 것은 실패하고, 네트의 보존하는 것이 필요 및 충분입니다.
구체적으로, 함수 f: X → Y는, 만약 X 안의 수열 \((x_n)\)이 극한 x에 수렴할 때마다, 수열 \((f(x_n))\)은 f(x)로 수렴하면, 수열적으로 연속(sequentially continuous:점렬 연속)입니다. 따라서 수열적으로 연속 함수는 "수열적 극한을 보존합니다". 모든 각 연속 함수는 수열적으로 연속입니다. 만약 X가 첫번째-셀 -수-있는 공간(first-countable space)이고 셀-수-있는 선택(countable choice)이 유지되면, 역도 역시 유지됩니다: 수열적 극한을 보존하는 임의의 함수는 연속입니다. 특히, 만약 X가 메트릭 공간이면, 수열적 연속성과 연속성은 동등합니다. 비-첫번째-셀-수-있는 공간에 대해, 수열적 연속성은 연속성보다 엄격하게 더 약할 수 있습니다. (두 속성이 동등한 것에 대해 공간은 수열적 공간(sequential space)이라고 불립니다.) 이것은 일반적인 토폴로지적 공간에서 수열 대신에 네트의 고려에 동기를 부여합니다. 연속 함수는 네트의 극한을 보존하고, 사실 이 속성은 연속 함수를 특징 짓습니다.
Closure operator definition
토폴로지적 공간의 열린 부분-집합을 지정하는 대신에, 토폴로지는 임의의 부분-집합 A ⊆ X에 그의 클로저(closure)를 할당하는, (cl로 표시되는) 클로저 연산자(closure operator), 또는 X의 임의의 부분-집합 A에 그의 내부(interior)를 할당하는, (int로 표시되는) 내부 연산자(interior operator)에 의해 역시 결정될 수 있습니다. 이들 용어에서, 토폴로지적 공간 사이의 함수
\(\quad\)\(f\colon (X,\mathrm{cl}) \to (X' ,\mathrm{cl}')\)
는 위의 의미에서 연속인 것과 X의 모든 부분-집합 A에 대해 다음인 것은 필요충분 조건입니다:
\(\quad\)\(f(\mathrm{cl}(A)) \subseteq \mathrm{cl}'(f(A)).\)
즉 말하자면, 임의의 부분-집합 A의 클로저 안에 있는 X의 임의의 원소 x가 주어지면, f(x)는 f(A)의 클로저에 속합니다. 이것은, X'의 모든 부분-집합 A'에 대해, 다음을 요구하는 것과 동등합니다:
\(\quad\)\(f^{-1}(\mathrm{cl}'(A')) \supseteq \mathrm{cl}(f^{-1}(A')).\)
게다가,
\(\quad\)\(f\colon (X,\mathrm{int}) \to (X' ,\mathrm{int}') \)
은 연속인 것과 Y의 임의의 부분 집합 A'에 대해 다음인 것은 필요충분 조건입니다:
Properties
만약 f: X → Y와 g: Y → Z가 연속이면, 그래서 합성 g ∘ f: X → Z도 마찬가지입니다. 만약 f: X → Y가 연속이고
- X가 컴팩트(compact)이면, f(X)는 컴팩트입니다.
- X가 연결된(connected) 것이면, f(X)는 연결된 것입니다.
- X가 경로-연결된 것이면, f(X)는 경로-연결된 것입니다.
- X가 린델뢰프(Lindelöf)이면, f(X)는 린델뢰프입니다.
- X가 분해-가능(separable)이면, f(X)는 분해-가능입니다.
고정된 집합 X 위의 가능한 토폴로지는 부분 순서화(partially ordered)입니다: 토폴로지 \(\tau_1\)은, 만약 \(\tau_1\)에 관한 모든 각 열린 부분-집합이 \(\tau_2\)에 관해 역시 열려 있으면, 또 다른 토폴로지 \(\tau_2\)보다 엉성하다(coarser)고 말합니다 (표기법: \(\tau_1\) ⊆ \(\tau_2\)). 그런-다음, 항등 맵(identity map)
\(\quad\)\(id_x: (X, \tau_2) \to (X, \tau_1)\)
이 연속인 것과 \(\tau_1\) ⊆ \(\tau_2\)인 것은 필요충분 조건입니다 (토폴로지의 비교(comparison of topologies)를 역시 참조하십시오). 보다 일반적으로, 연속 함수
\(\quad\)\((X, \tau_X) \rightarrow (Y, \tau_Y)\)
는, 만약 토폴로지 \(\tau_Y\)가 엉성한 토폴로지(coarser topology)에 의해 대체되고/대체되거나 \(\tau_X\)가 미세한 토폴로지(finer topology)에 의해 대체되면, 연속에 머무릅니다.
Homeomorphisms
연속 맵의 개념과 대칭은 열린 맵(open map)으로, 이것은 열린 집합의 이미지가 열려 있는 것입니다. 사실, 만약 열린 맵 f가 역 함수(inverse function)를 가지면, 그 역함수는 연속이고, 만약 연속 맵 g가 역함수를 가지면, 그 역함수는 열려 있습니다. 두 토폴로지적 공간 사이의 전단사(bijective) 함수 f가 주어지면, 역함수 \(f^{-1}\)은 연속일 필요는 없습니다. 연속 역함수를 갖는 전단사 연속 함수는 위상-동형(homomorphism)으로 불립니다.
만약 연속 전단사는 그의 도메인(domain)으로 컴팩트 공간(compact space)을 갖고 그의 코도메인(codomain)이 하우스도르프(Hausdorff)이면, 그것은 하나의 위상-동형입니다.
Defining topologies via continuous functions
X가 토폴로지적 공간이고 (지정된 토폴로지없이) S가 집합인, 다음 함수가 주어지면:
\(\quad\)\(f\colon X \rightarrow S, \)
S 위의 마지막 토폴로지(final topology)은 S의 열린 집합을, \(f^{-1}(A)\)가 X에서 열린 것에 대해 S의 그들의 부분-집합 A로 설정함으로써 정의됩니다. 만약 S가 존재하는 토폴로지을 가지면, f는 이 토폴로지에 관해 연속인 것과 존재하는 토폴로지가 S 위의 마지막 토폴로지보다 엉성한(coarser) 것은 필요충분 조건입니다. 따라서 마지막 포톨로지는 f를 연속으로 만드는 S 위의 가장-섬세한 토폴로지로 특징지을 수 있습니다. 만약 f가 전사(surjective)이면, 이 토폴로지는 f에 의해 정의된 동치 관계(equivalence relation) 아래에서 몫 토폴로지(quotient topology)로 정식적으로 식별됩니다.
이중으로, 집합 S에서 토폴로지적 공간 X으로 함수 f에 대해, S 위의 초기 토폴로지는 X의 어떤 열린 부분-집합 U에 대해 \(A = f^{-1}(U)\)를 만족하는 S의 모든 각 부분-집합 A를 지정하는 것에 의해 정의됩니다. 만약 S가 존재하는 토폴로지이면, f가 이 토폴로지에 관해 연속인 것과 존재하는 토폴로지가 S 위의 초기 토폴로지보다 더 미세한 것은 필요충분 조건입니다. 따라서 초기 토폴로지는 f를 연속으로 만드는 S 위의 가장-엉성한 토폴로지로 특징 지어질 수 있습니다. 만약 f가 단사이면, 이 토폴로지가, X의 부분-집합으로 보여지는, S의 부분공간 토폴로지(subspace topology)로 공식적으로 식별됩니다.
집합 S 위의 토폴로지는 모든 토폴로지적 공간 X으로 모든 연속 함수 \(S \rightarrow X\)의 클래스에 의해 고유하게 결정됩니다. 이중으로(Dually), 비슷한 아이디어는 맵 \(X \rightarrow S\)에 적용될 수 있습니다.
Related notions
다양한 다른 수학 영역은 연속성의 개념을 다르지만, 관련된 의미로 사용합니다. 예를 들어, 순서 이론(order theory)에서, 부분적으로 순서화 집합(partially ordered set) X와 Y의 특정 유형 사이의 순서-보존 함수 f: X → Y는, 만약 X의 각 방향화된 부분-집합 A에 대해, 우리가 sup(f(A)) = f(sup(A))를 가지면, 연속(continuious)입니다. 여기서 sup는, 각각, X와 Y 안의 순서화에 관해 상한(supremum)입니다. 연속성의 이 개념은 부분적으로 순서화 집합이 스콧 토폴로지(Scott topology)로 주어질 때 토폴로지적 연속성과 같습니다.
카테고리 이론(category theory)에서, 두 카테고리(category) 사이의 함수자(functor:함자)
\(\quad\)\(F\colon \mathcal C \rightarrow \mathcal D\)
는, 만약 그것이 작은 극한(limits)과 함께 교환되면, 연속(continuous)으로 불립니다. 즉 말하자면, \(\mathcal C\) 안의 대상의 임의의 작은 다이어그램에 대해 (즉, 클래스(class)와 반대인 것처럼, 집합 I에 의해 인덱스된) 다음입니다:
\(\quad\)\(\displaystyle \varprojlim_{i \in I} F(C_i) \cong F \left(\varprojlim_{i \in I} C_i \right)\).
연속성 공간(continuity space)은 메트릭 공간(metric space)과 포셋(posets:부분적으로 순서화 집합:partially ordered set)의 일반화이며, 이것은 콘태일(quantale)의 개념을 사용하고, 메트릭 공간 및 도메인(domain)의 개념을 통합하기 위해 사용될 수 있습니다.



