(고등학교) 두 원의 공통 외접선 예제와 해설

두 원 \(x^2+y^2=1\), \((x-2)^2+y^2=4\)에 동시에 접하는 접선의 방정식은 \(y=mx+n\)입니다. 두 상수 \(m,n\)에 대하여 \(30\left(m^2+n^2\right)\)의 값은?

해설: 이 문제에서, 특별한 것은 없지만, 몇 가지를 살펴볼 수 있습니다.
먼저, 두 원의 중심, (0,0), (2,0), 사이의 거리는 2이고, 반지름의 합, 1+2=3이고, 반지름의 차, 2–1=1이므로, 두 원은 두 점에서 만납니다. 그러므로, 공통외접선 2개를 그릴 수 있습니다.
첫 번째 방법은 원과 직선의 연립방정식이 중근을 갖는 경우로 접근합니다.
\(\quad\displaystyle x^2+(mx+n)^2-1=0,\;(x-2)^2+(mx+n)^2-4=0\)
이 두 식을 전개한 후, 동류항으로 정리하고, 판별식이 영이 되는 두 식을 다시 연립해서, \(m,n\)을 결정할 수 있습니다. 아마도 다른 방법과 비교해서 가장 시간이 많이 걸릴 것으로 추정됩니다.
두 번째 방법은 두 원의 중심에서 직선까지의 거리가 반지름과 각각 같아지는 식을 이용합니다.
\(\quad\displaystyle mx-y+n=0\;(0,0)\)
\(\quad\displaystyle mx-y+n=0\;(2,0)\)
직접 식을 적어보면,
\(\quad\displaystyle \frac{|n|}{\sqrt{m^2+1}}=1\)
\(\quad\displaystyle \frac{|2m+n|}{\sqrt{m^2+1}}=2\)
분모를 양쪽 변에 곱해서,
\(\quad\displaystyle |n|=\sqrt{m^2+1},\;|2m+n|=2\sqrt{m^2+1}\)
양쪽 변을 제곱해서 연립해야 하지만, 크게 계산이 줄 것으로 기대되지는 않습니다.

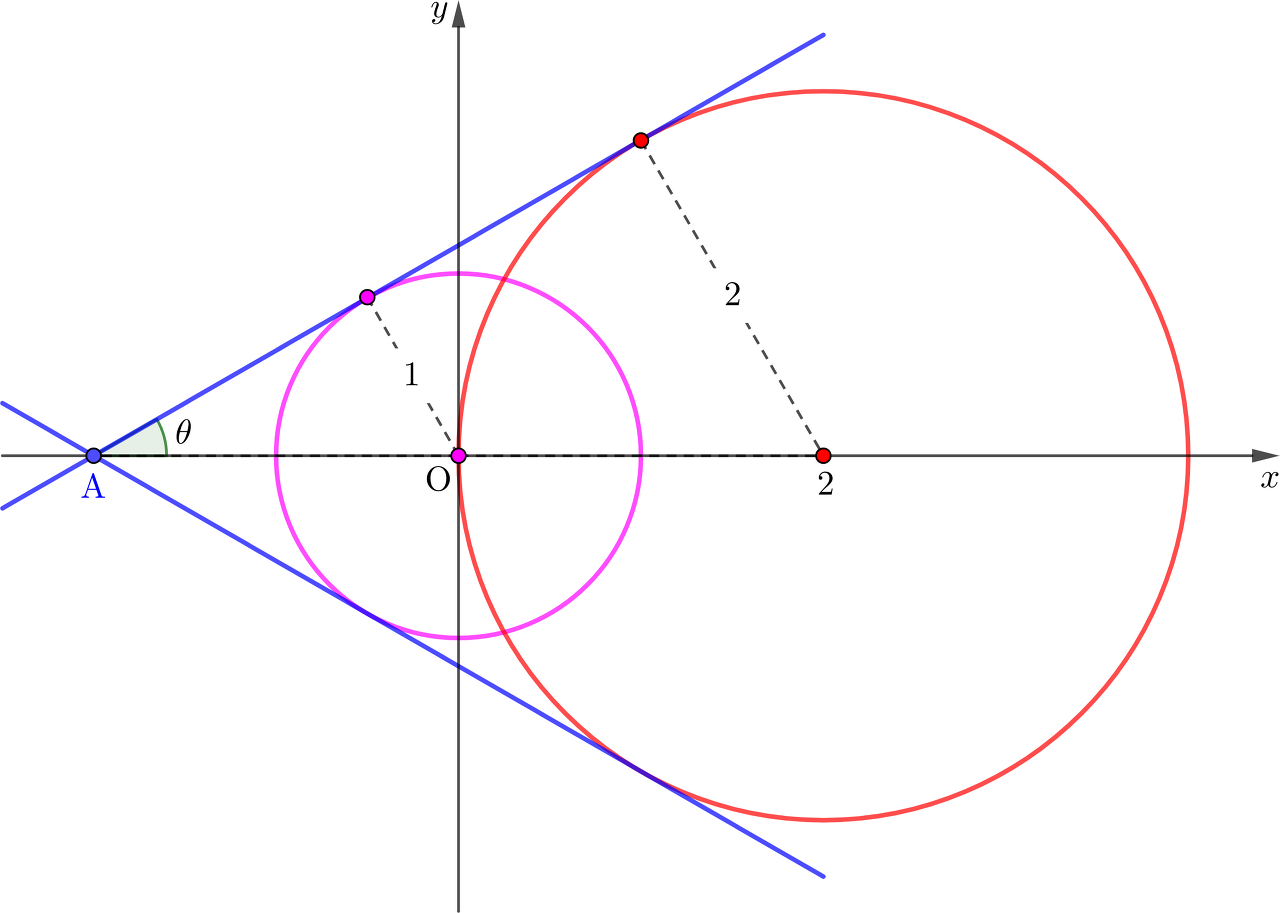
마지막으로, 그래프의 개형을 그려서, 기하학적으로 접근할 수 있습니다. 
그림과 같은 개형에서, 두 공통외접선의 교점, \(\mathrm A\)는, 그 점과 두 반지름으로 이루어지는 두 삼각형의 비가 반지름에 의해 1:2이므로, \(\mathrm{A}(-2,0)\)임을 알 수 있습니다.
더구나, 작은 삼각형에서 나머지 변의 길이는 피타고라스 정리에 의해 \(\sqrt{3}\)이고, 그러므로, 1의 대각은 \(30^\mathrm{o}\)임을 알 수 있습니다. 
따라서, 위쪽의 공통외접선은, \(x\)-축의 양의 방향과 이루는 각도가 \(30^\mathrm{o}\)이고, 지나는 점이 \(\mathrm{A}(-2,0)\)이므로,
\(\quad\displaystyle y=\frac{1}{\sqrt{3}}(x+2)\)
한편, 아래쪽으로 접하는 공통외접선은 \(x\)-축의 양의 방향과 이루는 각도가 \(-30^\mathrm{o}\), 지나는 점이 \(\mathrm{A}(-2,0)\)이므로,
\(\quad\displaystyle y=-\frac{1}{\sqrt{3}}(x+2)\)
또는, 위쪽의 직선과 \(x\)-축 대칭이므로, 어쨌든, 결과는 같습니다. 
\(\quad\displaystyle -y=\frac{1}{\sqrt{3}}(x+2)\)
일반적인 경우) 두 원의 중심이 좌표축 위에 있을 때, 공통외접선을 기하학적으로 구하는 방법은 다음과 같습니다. 예를 들어,
\(\quad\displaystyle (x-a)^2+y^2=r_1^2, (x-b)^2+y^2=r_2^2\)

여기서 \(a<b\)이고, \(r_1 < r_2\)이라고 두면, 그래프의 개형으로부터 다음과 같은 비례식을 얻을 수 있습니다.
\(\quad\displaystyle a-k:b-k=r_1:r_2\)
여기서 기하학적으로 \(k<a\)이고, \(k\)는 공통외접선이 \(x\)-축과 만나는 점입니다.
그런 다음 기울기는 다음의 과정으로 구해집니다.
먼저 티라고라스의 정리로부터
\(\quad\displaystyle q=\sqrt{(a-k)^2-r_1^2}\)
이 식은 위의 그림에서처럼, 작은 직각삼각형의 나머지 변입니다. 이것으로부터, 기울기의 정의와 두 닮음 삼각형의 비값에 따라,
\(\quad\displaystyle \frac{p}{a-k}=\frac{r_1}{q}\)
결국, 두 공통외접선은 다음과 같이 구해집니다:
\(\quad\displaystyle y=\pm\frac{r_1}{q}(x-k)\)
아마도 같은 상황에서 공통내접선이 발생한다면, 이와 같은 방법을 이용해서 구할 수 있을 것으로 여겨집니다. 물론, 축의 위치가 \(y\)-축으로 바뀌면, 이것도 비슷한 과정으로 구해질 것으로 기대됩니다.
공통내접선이 발생하면, 위와 같은 조건에서, \(x\)-축과 만나는 점과 다음과 같이 구해집니다:
\(\quad\displaystyle b-k:k-a=r_2:r_1\)
이고, 기울기를 구하는 과정은 공통외접선과 동일하고, 어차피 \(x\)-축 대칭으로 2개의 직선이 만들어지므로, 기울기의 크기가 오직 중요합니다.

식은 같지만, \(k\)의 값이 달라지기 때문에, 기울기는 달라집니다. 공통내접선에선는 \(a<k<b\)의 크기 순서로 만들어집니다.

한편, 극선의 방정식(polar-pole relation)을 알고 있다면, 극선의 방정식과 원의 교점, 즉, 접점을 구해서 접근할 수 있습니다. 이때, 역시 반지름의 비로 \(x\)-절편을 면저 구해야 극선의 방정식을 구할 수 있습니다.