삼각법(trigonometry)에서, (역시 코사인 공식(cosine formula) 또는 코사인 규칙(cosine rule), 또는 알-카시(al-Kashi)의 정리로 알려진) 코사인의 법칙(law of cosines)은 삼각형(triangle)의 변의 길이를 그것의 각도(angle) 중 하나의 코사인(cosine)과 관련시킵니다. 그림 1에서와 같이 표기법을 사용하여, 코사인의 법칙은 다음임을 말합니다:
\(\quad c^2 = a^2 + b^2 - 2ab\cos\gamma,\)
여기서 γ는 길이 a와 b인 변 사이의 포함된 각도를 나타내고 길이 c의 변의 반대편입니다.
코사인의 법칙은, 직각 삼각형(right triangles)에 대해 오직 유지되는, 피타고라스 정리(Pythagorean theorem)를 일반화합니다: 만약 각도 γ가 직각 (측정 90도(degree), 또는 \(\tfrac{\pi}{2}\) 라디안(radian))이면, cos γ = 0이고, 따라서 코사인의 법칙은 피타고라스의 정리(Pythagorean theorem)로 줄어듭니다:
\(\quad c^2 = a^2 + b^2.\)
코사인의 법칙은 두 변과 그들로 둘러싸인 각도를 알려져 있을 때 삼각형의 세 번째 변을 계산하는 것에 유용하고, 만약 세 변을 모두 알려져 있으면, 삼각형의 각도를 계산하는 것에서 유용합니다.
History
비록 코사인(cosine)의 개념이 유클리드(Euclid) 시대에 아직 개발되지 않았을지라도, 기원전 3세로 거슬러 올라가는, 그의 원론(Elements)은 코사인의 법칙과 거의 동등한 초기 기하학 정리를 포함합니다. (음 및 양의 코사인의 두 경우에 해당하는) 둔각 삼각형 및 예각 삼각형(obtuse triangles and acute triangles)의 경우는 책 2의 제안 12와 13에서, 별도로 취급됩니다. 삼각 함수와 대수학 (특히 음의 숫자)은 유클리드의 시대에 존재하지 않았으며, 그 명제는 보다 기하학적 운치를 가집니다:
제안 12
둔-각 삼각형에서, 둔각을 끼고-있는 변에 대한 젝보은 둔각을 포함하는 변에 대한 제곱보다 둔각에 대한 각도의 하나에 의해 포함된 직사각형, 즉, 수직으로 떨어지고, 둔각을 향한 수직에 의해 밖에서 직선을 자른 것의 두 배만큼 큽니다.— 유클리드의 원론.
그림 2에서 처럼 표기법을 사용하여, 유클리드의 명제는 다음 공식에 의해 표현될 수 있습니다:
\(\quad AB^2 = CA^2 + CB^2 + 2 (CA)(CH).\)
이 공식은 CH = (CB) cos(π − γ) = −(CB) cos γ임을 주목함으로써 코사인 법칙으로 변환될 수 있습니다. 제안 13은 예각 삼각형에 대해 전체적으로 유사한 명제를 포함합니다.
유클리드의 원론은 코사인의 법칙의 발견에 대해 길을 열었습니다. 15세기에서, 잠쉬드 알-캐시(Jamshīd al-Kāshī), 페르시아 수학자이자 천문학자는 삼각분할(triangulation)에 적합한 형식에서 코사인의 법칙의 최초의 명시적 명제를 제공했습니다. 그는 정확한 삼각법 테이블을 제공했고 현대의 사용에 적합한 형식으로 정리를 표현했습니다. 1990년대, 프랑스(France)에서, 코사인의 법칙은 여전히 Théorème d'Al-Kashi라고 참조됩니다.
그 정리는 16세기에 프랑수아 비에트(François Viète)에 의해 서구 세계(Western world)에서 대중화되었습니다. 19세기 초에서, 현대의 대수 표기법은 코사인 법칙을 현재의 기호적 형식으로 쓰는 것을 허용합니다.
Applications
정리는, 삼각형 또는 원을 푸는 것에 대해, 즉, 다음을 찾기 위해 삼각분할(triangulation)에서 사용됩니다 (그림 3을 참조하십시오):
- 만약 우리가 두 변과 그들 사이의 각도를 알고 있으면 삼각형의 세 번째 변을 구할 수 있습니다:
- \(\,c = \sqrt{a^2+b^2-2ab\cos\gamma}\,;\)
- 만약 우리가 세 변을 알고 있으면, 삼각형의 각도를 구할 수 있습니다:
- \(\,\gamma = \arccos\left(\frac{a^2+b^2-c^2}{2ab}\right)\,;\)
- 만약 우리가 두 변과 그들의 하나에 대한 반대편 각도를 알고 있으면 삼각형의 세 번째 변을 구할 수 있습니다 (우리는 그것이 직각 삼각형(right triangle)이면 이것을 행하기 위해 피타고라스 정리(Pythagorean theorem)를 역시 사용할 수 있습니다):
- \(\, a=b\cos\gamma \pm \sqrt{c^2 -b^2\sin^2\gamma}\,.\)
이들 공식은 만약 삼각형이 매우 예각이면, 즉 만약 c가 a와 b에 상대적으로 작거나 γ가 1에 비해 작으면, 부동-점(floating point) 계산에서 높은 반올림 오차(round-off error)를 생성합니다. 심지어 각도의 코사인에 대해 일보다 약간 더 큰 결과를 얻는 것이 가능합니다.
세 번째 공식은 이차 방정식(quadratic equation) \(a^2-2ab\cos\gamma + b^2-c^2=0\)에서 a에 대해 푸는 것의 결과입니다. 이 방정식은 데이터에 주어진 가능한 삼각형의 숫자에 해당하는 2, 1, 또는 0 양수 해를 가질 수 있습니다. 만약 b sin γ < c < b이면 두 양수 해를 가질 것이고, 만약 c = b sin γ이면, 오직 하나의 양수, 및 만약 c < b sin γ이면 양수 해를 가지지 않을 것입니다. 이들 다른 경우는 변-변-각도 합동 모호성(side-side-angle congruence ambiguity)에 의해 역시 설명됩니다.
Proofs
Using the distance formula
길이 a, b, c의 변을 갖는 삼각형을 생각해 보십시오. 여기서 θ는 길이 c의 변 반대편 각도의 측정입니다. 이 삼각형은, 그림 4에서 보인 것처럼 삼각형의 3 점의 성분을 그림으로써, C에서 원점을 갖는 가장자리 a와 정렬된 데카르트 좌표 시스템(Cartesian coordinate system) 위에 배치될 수 있습니다:
\(\quad A = (b \cos\theta, b \sin\theta), B = (a, 0), \text{ and } C = (0, 0).\)
\(\quad c = \sqrt{(a - b \cos\theta)^2 + (0 - b \sin\theta)^2}.\)
양쪽 변을 제곱하고 간단히 하면,
\(\quad \begin{align}
c^2 & {} = (a - b \cos\theta)^2 + (- b \sin\theta)^2 \\
c^2 & {} = a^2 - 2 a b \cos\theta+ b^2 \cos^2 \theta+ b^2 \sin^2 \theta\\
c^2 & {} = a^2 + b^2 (\sin^2 \theta+ \cos^2 \theta) - 2 a b \cos\theta\\
c^2 & {} = a^2 + b^2 - 2 a b \cos\theta.
\end{align}\)
이 증명의 장점은 삼각형이 예각, 직각, 또는 둔각일 때에 대해 다른 경우의 고려사항을 요구하지 않는다는 것입니다.
Using trigonometry
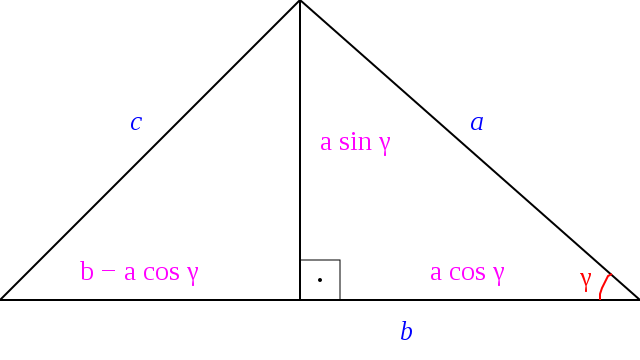
점 C를 통해 변 c 위로 수직(perpendicular)으로 내리면, 삼각형의 고도(altitude)를 형성하며, 변 c는 두 조각으로 나뉩니다. 사인과 코사인의 정으로부터 변 변 c는 다음과 같이 표현됩니다: (그림 5를 참조하십시오)
\(\quad c=a\cos\beta+b\cos\alpha.\)
(이것은 α 또는 β가 둔각일 때 여전히 참이며, 이 경우에서 수직선은 삼각형의 밖에 떨어집니다.) 양쪽 변에 c를 곱하면 다음을 산출합니다:
\(\quad c^2 = ac\cos\beta + bc\cos\alpha.\)
삼각형의 두 다른 고도를 고려하면 다음을 산출합니다:
\(\quad a^2 = ac\cos\beta + ab\cos\gamma,\)
\(\quad b^2 = bc\cos\alpha + ab\cos\gamma.\)
후자 두 방정식을 더하면 다음을 제공합니다:
\(\quad a^2 + b^2 = ac\cos\beta + bc\cos\alpha + 2ab\cos\gamma.\)
마지막 방정식으로부터 첫 번째 방정식을 빼면 우리는 다음의 결과를 가집니다:
\(\quad a^2 + b^2 - c^2 = ac\cos\beta + bc\cos\alpha + 2ab\cos\gamma - ( ac\cos\beta + bc\cos\alpha )\)
이것은 다음으로 단순화됩니다:
\(\quad c^2 = a^2 + b^2 - 2ab\cos\gamma.\)
이 증명은 다양한 각도의 코사인을 자체에서 량으로 처리하는 삼각법(trigonometry)을 사용합니다. 각도의 코사인은 임의의 직각 삼각형에서 해당 각도를 둘러싸는 두 변 사이의 관계를 표현한다는 사실을 사용합니다. 다른 증명 (아래)은 a cos γ와 같은 표현을 단지 특정 선분의 길이에 대한 레이블로 취급한다는 점에서 보다 기하학적입니다.
많은 증명이 둔각과 예각 γ의 경우를 별도로 처리합니다.
Using the Pythagorean theorem
Case of an obtuse angle
유클리드(Euclid)는 보이는 그림에서 두 직각 삼각형 (AHB and CHB)의 각각에 피타고라스 정리(Pythagorean theorem)를 적용함으로써 이 정리를 입증했습니다. d를 선분 CH를 나타내기 위해 및 높이 height BH에 대해 h를 사용하면, 삼각형 AHB는 다음을 제공합니다:
\(\quad ^2 = (b+d)^2 + h^2,\)
그리고 삼각형 CHB는 다음을 제공합니다:
\(\quad d^2 + h^2 = a^2.\)
첫 번째 방정식을 전개(Expanding)하면 다음을 제공합니다:
\(\quad c^2 = b^2 + 2bd + d^2 +h^2.\)
두 번째 방정식에 이것을 대체하면, 다음 것이 획득될 수 있습니다:
\(\quad c^2 = a^2 + b^2 + 2bd.\)
이것이 원론(Elements)의 책 2로부터 유클리드의 제안 12입니다. 이것을 코사인의 법칙의 현대 형식으로 변환하기 위해, 다음임을 주목하십시오:
\(\quad d = a\cos(\pi-\gamma)= -a\cos\gamma.\)
Case of an acute angle
유클리드의 제안 13의 그의 증명은 발의안 제안 12의 그의 증명과 같은 선을 따라 진행됩니다: 그는 각도 γ를 둘러싸는 변 중 하나 위로 수직을 떨어뜨림으로써 형성된 오른쪽 삼각형 둘 다에 피타고라스 정리를 적용하고 단순화하기 위해 이항 정리를 사용합니다.
Another proof in the acute case
더 삼각법을 사용하여, 코사인의 법칙은 오직 한번 피타고라스 정리를 사용함으로써 추론될 수 있습니다. 사실, 그림 6의 왼쪽 변에 대한 직각 삼각형을 사용함으로써, 다음임을 보일 수 있습니다:
\(\quad \begin{align}
c^2 & {} = (b-a\cos\gamma)^2 + (a\sin\gamma)^2 \\
& {} = b^2 - 2ab\cos\gamma + a^2\cos^2\gamma+a^2\sin^2\gamma \\
& {} = b^2 + a^2 - 2ab\cos\gamma,
\end{align}\)
삼각 항등식(trigonometric identity)을 사용하여,
\(\quad \cos^2\gamma + \sin^2\gamma = 1.\)
이 증명은 만약 b < a cos(γ)이면 약간 수정이 필요합니다. 이 경우에서, 피타고라스 정리가 적용되는 직각 삼각형은 삼각형 ABC의 밖으로 이동합니다. 이것이 계산에 미치는 유일한 영향은 양 b − a cos(γ)가 a cos(γ) − b로 대체된다는 것입니다. 이 양은 제곱을 통해 오직 계산에 들어가므로, 증명의 남은 것은 영향을 받지 않습니다. 어쨌든, 이 문제는 β가 둔각일 때 오직 발생하고, γ의 이등분선에 대한 삼각형을 반사함으로써 피해질 수 있습니다.
그림 6을 참조하면, 만약 변 a의 반대쪽 각도가 α이면 다음임을 주목할 가치가 있습니다:
\(\quad\displaystyle \tan\alpha = \frac{a\sin\gamma}{b-a\cos\gamma}.\)
이것은 두 변과 포함된 각도가 주어질 때 두 번째 각도의 직접 계산에 대해 유용합니다.
Using Ptolemy's theorem
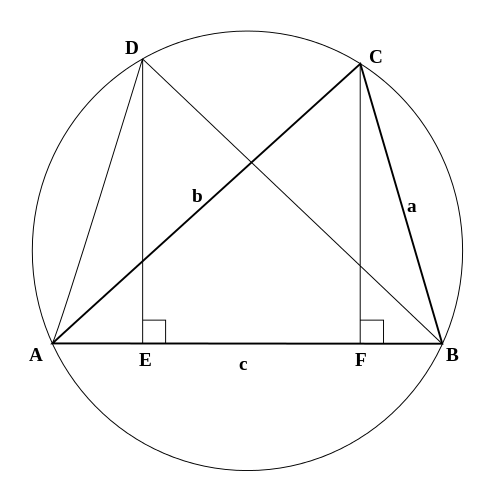
그림을 참조하여, 변 AB = c, BC = a 및 AC = b를 갖는 삼각형 ABC는 보인 것처럼 둘레-원 내부에 그려집니다. 삼각형 ABD는 AD = BC 및 BD = AC를 갖는 삼각형 ABC와 합동으로 구성됩니다. D와 C로부터 수직선은 각각 E와 F에서 밑변 AB와 만납니다. 그런-다음:
\(\quad \begin{align}
& BF=AE=BC\cos\hat{B}=a\cos\hat{B} \\
\Rightarrow \ & DC=EF=AB-2BF=c-2a\cos\hat{B}.
\end{align}\)
이제 코사인의 법칙은 프톨레마이오스의 정리(Ptolemy's theorem)를 순환 사변형(cyclic quadrilateral) ABCD에 간단하게 적용하여 렌더링됩니다:
\(\quad \begin{align}
& AD \times BC + AB \times DC = AC \times BD \\
\Rightarrow \ & a^2 + c(c-2a\cos\hat{B})=b^2 \\
\Rightarrow \ & a^2+c^2-2ac \cos\hat{B}=b^2.
\end{align}\)
명백하게 만약 각도 B가 직각(right)이면, ABCD는 직사각형이고 프톨레마이오스 정리의 적용은 피타고라스 정리(Pythagorean theorem)를 산출합니다.
\(\quad a^2+c^2=b^2.\quad\)
By comparing areas
우리는 넓이(area)를 계산함으로써 코사인의 법칙을 역시 입증할 수 있습니다. 각도 γ가 둔각이 됨에 따라 부호의 변경은 필연적인 경우 구별을 만듭니다.
다음임을 기억해 내십시오:
- \(a^2, b^2\), 및 \(c^2\)는 각각 변 a, b, 및 c를 갖는 정사각형의 넓이입니다;
- 만약 γ가 예각이면, ab cos γ는 \(\gamma' = \tfrac{\pi}{2} -\ gamma\)의 각도를 형성하는 변 a와 b를 갖는 평행-사변형(parallelogram)의 넓이입니다;
- 만약 γ가 둔각이고, 따라서 cos γ가 음수이면, −ab cos γ는 \(\gamma' = \gamma -\tfrac{\pi}{2}\)의 각도를 형성하는 변 a와 b를 갖는 평행-사변형(parallelogram)의 넓이입니다.
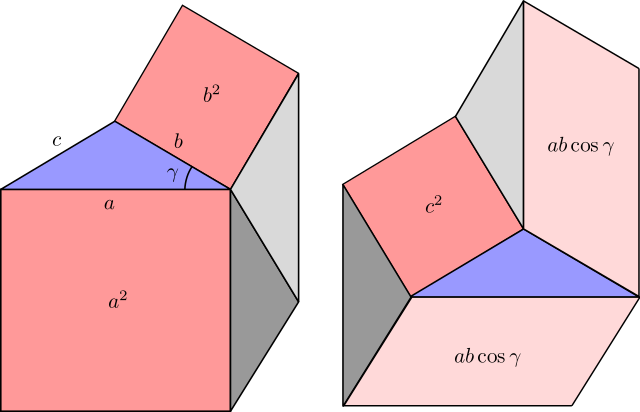
예각 경우. 그림 7a는 코사인의 법칙의 증명을 산출하기 위해 (두 다른 방법으로) 칠각형(heptagon)을 작은 조각으로 잘라낸 것을 보여줍니다. 다양한 조각은 다음입니다:
- 분홍색으로, 왼쪽에 넓이 \(a^2, b^2\), 및 오른쪽에 넓이 \(2ab \cos \gamma\)와 \(c^2\);
- 파란색으로, 왼쪽과 오른쪽에 삼각형 ABC;
- 회색으로, 보조 삼각형, 모두 ABC와 합동(congruent), 왼쪽과 오른쪽 둘 다에서 같은 숫자 (즉, 2)입니다.
왼쪽과 오른쪽에 넓이의 상등은 다음을 제공합니다:
\(\quad a^2 + b^2 = c^2 + 2ab\cos\gamma\,.\)
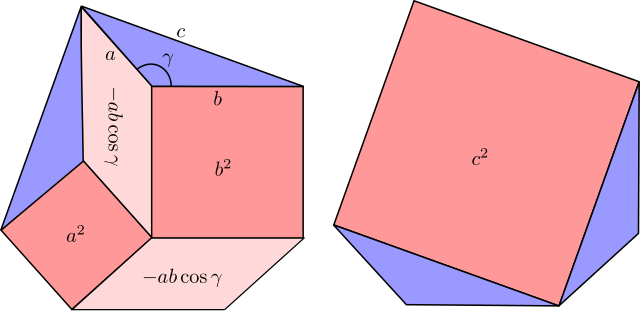
둔각 경우. 그림 7b는 두 다른 방법으로 육각형(hexagon)을 더 작은 조각으로 자르고, 각도 γ가 둔각인 경우에서 코사인의 법칙의 증명을 산출합니다. 우리는 다음을 가집니다:
- 분홍색으로, 왼쪽에 넓이 \(a^2, b^2\), 및 \(-2ab \cos \gamma\) 및 오른쪽에 \(c^2\);
- 파란색으로, 왼쪽, 마찬가지로 오른쪽에 삼각형 ABC 두 번입니다.
왼쪽과 오른쪽에 넓이의 상등은 다음을 제공합니다:
\(\quad a^2 + b^2 - 2ab\cos(\gamma) = c^2.\)
엄격한 증명은 다양한 모양이 합동(congruent)이고 따라서 같은 넓이를 가지는 증명을 포함해야 합니다. 이것은 합동 삼각형(congruent triangles)의 이론을 사용합니다.
Using geometry of the circle
원의 기하학(geometry of the circle)을 사용하면, 단독으로 피타고라스 정리를 사용하는 것보다 보다 기하학적(geometric) 증명을 제공할 수 있습니다. 대수적(Algebraic) 조작 (특히 이항 정리(binomial theorem))을 피합니다.
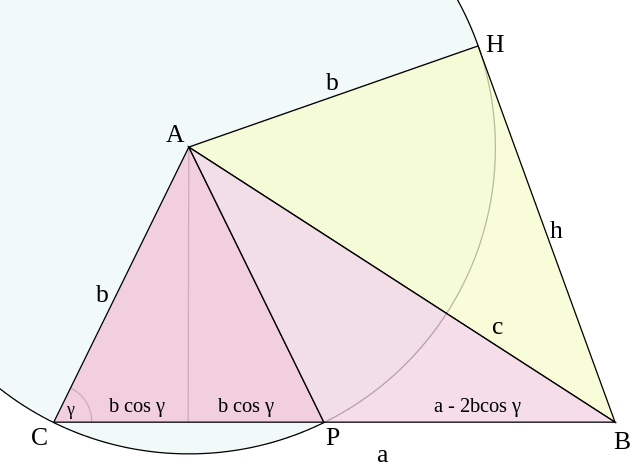
예각 γ의 경우, 여기서 a > 2b cos γ. A로부터 a = BC 위로 수직(perpendicular)으로 떨어뜨려, 길이 b cos γ의 선분을 만드십시오. 직각 삼각형(right triangle)을 이등변 삼각형(isosceles triangle) ACP를 형성하기 위해 복제하십시오. 중심 A와 반지름 b를 가진 원(circle), 및 B를 통과하는 그것의 접선(tangent) h = BH를 구성하십시오. 접선 h는 반지름 b와 직각을 형성하므로 (유클리드의 원론: 책 3, 제안 18; 또는 여기를 참조하십시오), 그림 8에서 노란 삼각형은 직각입니다. 다음을 얻기 위해 피타고라스 정리(Pythagorean theorem)를 적용하십시오:
\(\quad c^2 = b^2 + h^2.\)
그런-다음 접선 가름선 정리(tangent secant theorem) (유클리드 원론: 책 3, 제안 36)를 사용하며, 이것은 원 밖의 점 B를 통한 접선의 제곱은 B를 통과하는 임의의 가름선(secant)에 생성된 (B로부터) 두 선분의 곱과 같습니다. 현재의 경우에서: \(BH^2 = BC \cdot BP\), 또는
\(\quad h^2 = a(a - 2b\cos\gamma).\)
이전 방정식을 대체하면 코사인의 법칙을 제공합니다:
\(\quad c^2 = b^2 + a(a - 2b\cos\gamma).\)
\(h^2\)은 원에 관한 점 B의 거듭제곱(power)임을 주목하십시오. 피타고라스 정리와 접선 가름선 정리의 사용은 점의 거듭제곱 정리(power of a point theorem)를 단일 적용에 바뀔 수 있습니다.
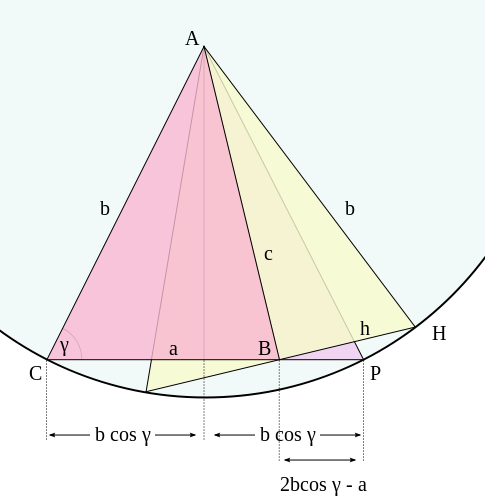
예각 γ의 경우, 여기서 a < 2b cos γ. A로부터 a = BC 위로 수직(perpendicular)으로 떨어뜨려, 길이 b cos γ의 선분을 만드십시오. 직각 삼각형(right triangle)을 이등변 삼각형(isosceles triangle) ACP를 형성하기 위해 복제하십시오. 중심 A와 반지름 b을 갖는 원(circle), 및 그것의 절반이 h = BH인 c = AB에 수직으로 B를 통과하는 현(chord)을 구성하십시오. 피타고라스 정리(Pythagorean theorem)를 다음을 얻기 위해 적용하십시오:
\(\quad b^2 = c^2 + h^2.\)
이제 현 정리(chord theorem) (유클리드의 원론: 책 3, 제안 35)을 사용하며, 이것은 만약 두 현이 교차하면, 한 현에서 얻어진 두 선분의 곱은 나머지 다른 현에서 얻어진 두 선분의 곱과 같음을 말합니다. 현재 경우에서: \(BH^2 = BC \cdot BP\), 또는
\(\quad h^2 = a(2b\cos\gamma - a).\)
이전 방정식에 대체하면 코사인의 정리를 제공합니다:
\(\quad b^2 = c^2 + a(2b\cos\gamma - a)\,.\)
원에 관한 점 B의 거듭제곱은 음의 값 \(-h^2\)을 가짐을 주목하십시오.
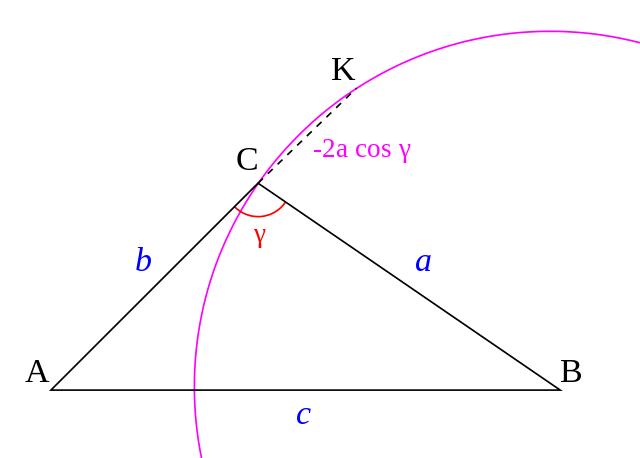
둔각 γ의 경우. 이 증명은 접선 또는 현을 구성함으로써 얻어진 보조 삼각형없이 직접 점의 거듭제곱 정리를 사용합니다. 중심 B와 반지름 a를 갖는 원을 구성하고 (그림 9 참조하십시오), 이것은 C와 K에서 A와 C를 통과하는 가름선(secant)과 교차합니다. 원에 관한 점 A의 거듭제곱(power)은 \(AB^2 -BC^2\)과 \(AC \cdot AK\) 둘 다와 같습니다. 그러므로,
\(\quad \begin{align}
c^2 - a^2 & {} = b(b + 2a\cos(\pi - \gamma)) \\
& {} = b(b - 2a\cos\gamma),
\end{align}\)
이것은 코사인의 법칙입니다.
(음수(negative numbers)를 선분의 길이로 허용하는) 선분에 대해 대수적 측정을 사용하면, 둔각 (CK > 0) 및 예각 (CK < 0)의 경우는 동시에 처리될 수 있습니다.
Using the law of sines
사인의 법칙(law of sines)을 사용하고 삼각형의 각도가 합해서 180도가 되어야 한다는 것을 앎으로써, 우리는 다음 방정식의 시스템을 가집니다 (세 미지수는 각도입니다):
\(\quad\displaystyle \frac{c}{\sin \gamma}=\frac{b}{\sin \beta},\)
\(\quad\displaystyle \frac{c}{\sin \gamma}=\frac{a}{\sin \alpha},\)
\(\quad\displaystyle \alpha + \beta + \gamma = \pi.\)
그런-다음, 세 번째 시스템의 방정식을 사용함으로써, 우리는 두 변수에서 두 방정식의 시스템을 얻습니다:
\(\quad\displaystyle \frac{c}{\sin \gamma}=\frac{b}{\sin (\alpha + \gamma)},\)
\(\quad\displaystyle \frac{c}{\sin \gamma}=\frac{a}{\sin \alpha},\)
여기서 우리는 보충 각도(supplementary angle)의 사인은 각도의 사인과 같다는 삼각법 속성을 사용했습니다.
항등식을 사용하면 (각도 합 및 차이 항등식(Angle sum and difference identities)을 참조하십시오)
\(\quad\displaystyle \sin (\alpha + \gamma)=\sin \alpha \cos \gamma + \sin \gamma \cos \alpha\)
다음으로 이어집니다:
\(\quad\displaystyle c (\sin \alpha \cos \gamma + \sin \gamma \cos \alpha)=b \sin \gamma,\)
\(\quad\displaystyle c \sin \alpha = a \sin \gamma.\)
전체 시스템을 cos γ로 나눔으로써, 우리는 다음을 가집니다:
\(\quad\displaystyle c (\sin \alpha + \tan \gamma \cos \alpha)=b \tan \gamma,\)
\(\quad\displaystyle \frac{c \sin \alpha}{\cos \gamma} = a \tan \gamma,\)
\(\quad\displaystyle \frac{c^2 \sin^2 \alpha}{\cos^2 \gamma}= a^2 \tan^2 \gamma.\)
따라서, 시스템의 첫 번째 방정식으로부터, 우리는 다음을 얻을 수 있습니다:
\(\quad\displaystyle \frac{c \sin \alpha}{b- c \cos \alpha}=\tan \gamma\)
이 표현을 부 번째 방정식에 대체하고 다음을 사용함으로써
\(\quad\displaystyle 1+\tan^2 \gamma=\frac{1}{\cos^2 \gamma}\)
우리는 하나의 변수를 갖는 하나의 방정식을 얻을 수 있습니다:
\(\quad\displaystyle c^2 \sin^2 \alpha \left[1+ \frac{c^2 \sin^2 \alpha}{(b- c \cos \alpha)^2} \right] = a^2 \cdot \frac{c^2 \sin^2 \alpha}{(b- c \cos \alpha)^2}\)
\((b-c \cos \alpha)^2\)을 곱함으로써, 우리는 다음 방정식을 얻을 수 있습니다:
\(\quad\displaystyle (b- c \cos \alpha)^2 + c^2 \sin^2 \alpha=a^2.\)
이것은 다음임을 의미합니다:
\(\quad\displaystyle b^2 - 2bc\cos\alpha +c^2 \cos^2 \alpha +c^2\sin^2\alpha=a^2.\)
피타고라스 항등식(Pythagorean identity)을 다시-회상하면, 우리는 코사인의 법칙을 얻습니다:
\(\quad\displaystyle a^2=b^2+c^2-2bc\cos\alpha.\)
Isosceles case
a = b일 때, 즉, 삼각형이 같은 각도 γ와 동일한 두 변을 갖는 이등변(isosceles)일 때, 코사인의 법칙이 크게 단순화됩니다. 즉, \(a^2+b^2 = 2a^2=2ab\)이기 때문에, 코사인의 법칙은 다음이 됩니다:
\(\quad\displaystyle \cos\gamma = 1 - \frac{c^2}{2a^2}\)
또는
\(\quad\displaystyle c^2 = 2a^2 (1 - \cos\gamma).\)
Analogue for tetrahedra
유사한 명제는 α, β, γ, δ를 사면체(tetrahedron)의 네 면의 넓이로 취함으로써 시작됩니다. 이면각(dihedral angle)을 \(\widehat{\beta\gamma}\) 등으로 나타냅니다. 그런-다음
\(\quad\displaystyle \alpha^2 = \beta^2 + \gamma^2 + \delta^2 - 2\left[\beta\gamma\cos\left(\widehat{\beta\gamma}\right) + \gamma\delta\cos\left(\widehat{\gamma\delta}\right) + \delta\beta\cos\left(\widehat{\delta\beta}\right)\right].\)
Version suited to small angles
각도, γ가 작고 인접한 변 a와 b가 비슷한 길이의 것일 때, 코사인의 법칙의 표준 형식의 오른쪽 변은 수치적 유효자리의 손실(loss of significance)에 대한 많은 정확성을 잃을 수 있습니다. 이것이 중요한 관심사인 상황에서, 헤벌사인 공식(haversine formula)과 유사한, 코사인의 법칙의 수학적으로 동등한 버전이 유용하게 입증될 수 있습니다:
\(\quad\displaystyle \begin{align}
c^2 &= (a - b)^2 + 4ab\sin^2\left(\frac{\gamma}{2}\right) \\
& = (a - b)^2 + 4ab\operatorname{haversin}(\gamma).
\end{align}
\)
무한소 각도의 극한에서, 코사인의 법칙은 원형 호 길이(circular arc length) 공식, c = a γ로 퇴화합니다.
In spherical and hyperbolic geometry
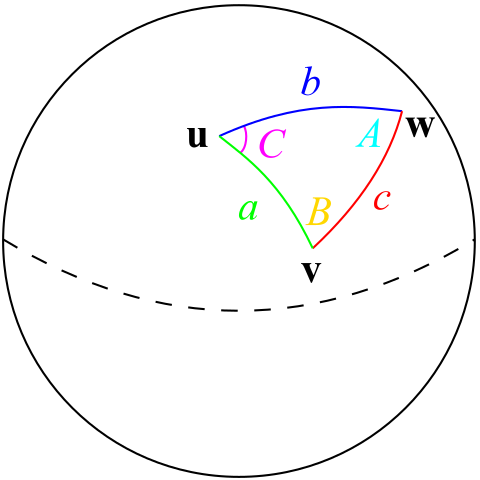
유클리드 평면에 대해 코사인의 법칙과 비슷한 버전은 단위 구 위에 및 쌍곡형 평면에서 역시 유지됩니다. 구형 기하학(spherical geometry)에서, 삼각형은 단위 구 위에 세 점 u, v, 및 w, 그들 점을 연결하는 큰 원(great circle)의 호에 의해 정의됩니다. 만약 이들 큰 원이 반대편 변 a, b, c를 가진 각도 A, B, 및 C를 만들면, 구형 코사인의 법칙(spherical law of cosines)은 다음 두 관계의 둘 다를 유지된다고 주장합니다:
\(\quad\displaystyle \begin{align}
\cos a &= \cos b\cos c + \sin b\sin c\cos A\\
\cos A &= -\cos B\cos C + \sin B\sin C\cos a.
\end{align}\)
쌍곡형 기하학(hyperbolic geometry)에서, 방정식의 쌍은 쌍곡형 코사인의 법칙(hyperbolic law of cosines)으로 집합적으로 알려져 있습니다. 그 첫 번째는 다음입니다:
\(\quad\displaystyle \cosh a = \cosh b\cosh c - \sinh b \sinh c \cos A\)
여기서 sinh와 cosh는 쌍곡 사인과 코사인(hyperbolic sine and cosine)이고, 그 두 번째는 다음입니다:
\(\quad\displaystyle \cos A = -\cos B \cos C + \sin B\sin C\cosh a.\)
유클리드 기하학에서 처럼, 우리는 코사인의 법칙을 변 a, b, c의 지식으로부터 각도 A, B, C를 결정하기 위해 사용될 수 있습니다. 유클리드 기하학과는 반대로, 전환은 비-유클리드 모델 둘 다에서 역시 가능합니다. 각도 A, B, C는 변 a, b, c를 결정합니다.
Unified formula for surfaces of constant curvature
두 함수 \(\cos_R\)와 \(\sin_R\)를 다음으로 정의하면,
\(\quad\displaystyle \cos_R(x) = \cos(x/R)\quad\) and \(\quad\sin_R(x) = R\cdot\sin(x/R)\)
평면(plane), 구(sphere) 및 유사-구(pseudosphere)에 대해 그 공식을 다음으로 통합하는 것을 허용합니다:
\(\quad\displaystyle \cos_R(BC) = \cos_R(AB)\cdot\cos_R(AC) + \frac{1}{R^2}\sin_R(AB)\cdot\sin_R(AC)\cdot\cos(\widehat{BAC}).\)
이 표기법에서, \(R\)은 복소수(complex number)이며, 표면의 곡률의 반지름(radius of curvature)을 나타냅니다.
- \(R \in \mathbb R\)에 대해, 표면은 반지름 \(R\)의 구(sphere)이고, 그것의 상수 곡률은 \(1/R^2\)와 같습니다;
- \(R = iR'\colon R' \in \mathbb R\)에 대해, 표면은 {{nowrap|\(1/R^2 = -1/R'^2\)와 같은}} 상수 곡률을 갖는 (허수) 반지름 \(R\)의 유사-구(pseudosphere)입니다.
- \(R \to \infty\)에 대해: 표면은 상수 영 곡률을 갖는 유클리드 평면(plane)으로 경향입니다.
비-유클리드 기하학에 대해 공식 확인하기
첫 번째 두 경우에서, \(\cos_R\)과 \(\sin_R\)은 모든 \(R \neq 0\)에 대해 전체 복소 평면(complex plane)에 걸쳐 잘-정의되고, 이전 결과를 검색하는 것은 간단합니다.
따라서, 반지름 \(1\)의 구에 대해,
\(\quad\displaystyle \cos(BC) = \cos(AB)\cdot\cos(AC) + \sin(AB)\cdot\sin(AC)\cdot\cos(\widehat{BAC})\).
마찬가지로, 반지름 \(i\)의 유사-구에 대해,
\(\quad\displaystyle \cosh(BC) = \cosh(AB)\cdot\cosh(AC) - \sinh(AB)\cdot\sinh(AC)\cdot\cos(\widehat{BAC}).\)
사실, \(\cosh(x) = \cos(x/i)\)과 \(\sinh(x) = i\cdot\sin(x/i)\)입니다.
유클리드 기하학의 극한에서 공식 확인하기
유클리드 평면에서, 위의 방정식에 대해 적절한 극한은 계산되어야 합니다:
\(\quad\displaystyle \cos_R(x) = \cos(x/R) = 1 - \frac{1}{2}\cdot \frac{x^2}{R^2} + o\left(\frac{1}{R^4}\right)\)
및
\(\quad\displaystyle \sin_R(x) = R\cdot\sin(x/R) = x + o\left(\frac{1}{R^3}\right)\).
유한 \(R\)에 대해 일반적신 공식에 이것을 적용하면 다음을 산출합니다:
\(\quad\displaystyle \begin{align}
1 - \frac{BC^2}{2R^2} + o\left[\frac{1}{R^4}\right] = {} & \left[1 - \frac{AB^2}{2R^2} + o\left(\frac{1}{R^4}\right)\right]\cdot\left[1 - \frac{AC^2}{2R^2} + o\left(\frac{1}{R^4}\right)\right] +\\[5pt]
& {} + \frac{1}{R^2}\left[AB + o\left(\frac{1}{R^3}\right)\right]\cdot\left[AC + o\left(\frac{1}{R^3}\right)\right]\cdot\cos(\widehat{BAC})
\end{align}\)
항을 모우고, \(-2R^2\)을 곱하고, \(R\to\infty\)를 취하면 예상된 공식을 산출합니다:
\(\quad\displaystyle BC^2 = AB^2 + AC^2 - 2\cdot AB \cdot AC \cdot\cos(\widehat{BAC}).\)
See also
- Law of sines
- Law of tangents
- Law of cotangents
- List of trigonometric identities
- Mollweide's formula
- Solution of triangles
External links
