(번역) Inverse trigonometric functions

Original article: w:Inverse trigonometric functions

 

수학(mathematics)에서, 역 삼각 함수 (때때로 역시 arcus functions, antitrigonometric functions 또는 cyclometric functions라고 불림)는 (적절하게 제한된 도메인(domain)을 갖는) 삼각 함수(trigonometric functions)의 역 함수(inverse function)입니다. 구체적으로 특별히, 그것들은 사인(sine), 코사인(cosine), 탄젠트(tangent), 코탄젠트(cotangent), 시컨트(secant), 및 코시컨트(cosecant) 함수의 역함수이고, 각도의 삼각 비율 중 임의의 것에서 각도를 얻기 위해 사용됩니다. 역 삼각 함수는 공학(engineering), 항해(navigation), 물리학(physics), 및 기하학(geometry)에서 널리 사용됩니다.

Notation

역 삼각 함수에 대해 몇 가지 표기법이 존재합니다. 가장 공통적인 관례는 arc- 접두사를 사용하여: arcsin(x), arccos(x), arctan(x), 등의 역 삼각 함수의 이름을 지정하는 것입니다. (이 관례는 이 기사 전체에서 사용됩니다.) 이 표기법은 다음 기하학적 관계에서 발생합니다: 라디안에서 측정할 때, θ 라디안의 각도는 그것의 길이가 rθ인 호에 해당할 것이며, 여기서 r은 원의 반지름입니다. 따라서 단위 원(unit circle)에서, "그것의 코사인이 x인 호"는 "그것의 코사인이 x인 각도"와 같은데, 왜냐하면 반지름에서 원호의 길이가 라디안에서 각도의 측정과 같기 때문입니다. 컴퓨터 프로그래밍 언어에서, 역 삼각 함수는 종종 asin, acos, atan의 축약형으로 호출됩니다.

1813년 존 허셜(John Herschel)에 의해 도입된, 표기법 ${\sin }^{-1}(x),{\cos }^{-1}(x),{\tan }^{-1}(x)$, 등은 영어 출처에서도 자주 사용되며, 훨씬 더 역시 확립된 ${\sin }^{[-1]}(x),{\cos }^{[-1]}(x),{\tan }^{[-1]}(x)$이 사용되었습니다–관례는 역함수(inverse function)의 표기법과 일치하며, 그것은 각 역 삼각 함수: ${\tan }^{-1}(x)=\{\arctan (x)+\pi k\mid k\in \mathbb{Z}\}$의 다중값(multivalued) 버전을 정의하기 위해 유용합니다. 어쨌든, 이것은 함수 합성보다 수치적 거듭제곱을 참조하는 (비록 오직 ${\sin }^2(x)$가, 대괄호없이, 실제로 공통적이지만) ${\sin }^{(}x)$와 같은 표현식에 대해 공통적인 의미론과 논리적으로 충돌하는 것처럼 보일 수 있고, 따라서 곱셈의 역(multiplicative inverse) 또는 역수(reciprocal) 및 합성적 역(compositional inverse) 사이의 혼란을 초래할 수 있습니다. 그 혼란은 각 역 삼각 함수가 자체의 이름–예를 들어, $(\cos (x){)}^{-1}=\sec (x)$를 가진다는 사실에 의해 다소 완화됩니다. 그럼에도 불구하고, 특정 저자들은 그것의 모호성 때문에 사용하지 말라고 조언합니다. 소수의 저자들에 의해 사용되는 또 다른 불안정한 관례는 ${}^{-1}$ 위첨자와 함께 대문자 첫 글자를 사용하는 것입니다: ${\text{Sin}}^{-1}(x),{\text{Cos}}^{-1}(x),{\text{Tan}}^{-1}(x)$, 등. 비록 그 의도는 곱셈 역수와의 혼동을 피하기 위한 것이지만, ${\sin }^{-1}(x),{\cos }^{-1}(x)$, 등, 또는, 더 나은, ${\sin }^{-1}x,{\cos }^{-1}x$, 등으로 표시되어야 하며, 그것은 차례로 또 다른 주요 모호성 원천을 생성합니다: 특히 많은 인기 있는 고급 프로그래밍 언어 (예를 들어, 월프럼 매스메티카와 시드니 대학의 MAGMA)는 표준 삼각 함수에 대해 같은 대문자 표현을 사용하고; 반면 다른 것들 (파이션 (예를 들어, SymPy와 NumPy), Matlab, MAPLE, 등)은 소문자를 사용한다는 사실에 비추어 볼 때 혼란을 초래될 수 있습니다.

따라서, 2009년 이래로, ISO 80000-2 표준은 역함수에 대해 "arc" 접두사만 지정해 왔습니다.

Basic concepts

Principal values

여섯 삼각 함수의 어떤 것도 일-대-일(one-to-one)이 아니기 때문에, 그것들은 역 함수를 가지기 위해 제한되어야 합니다. 그러므로, 역 함수의 결과 치역(range)은 원래 함수의 도메인의 적절한 (즉, 엄격한) 부분집합(subset)입니다.

예를 들어, 제곱근(square root) 함수 $y=\sqrt{x}$가 $y^2=x$에서 정의될 수 있는 것처럼 다중값 함수(multivalued function)의 의미에서 함수를 사용하여, 함수 $y=\arcsin (x)$는 $\sin (y)=x$가 되도록 정의됩니다. $-1\le x\le 1$를 갖는 주어진 실수 $x$에 대해, $\sin (y)=x$를 만족하는 여러 (사실, 셀-수-있는 무한(countably infinite)하게 많은) 숫자 $y$가 있습니다; 예를 들어, $\sin (0)=0$이지만, 역시 $\sin (\pi )=0,$ $\sin (2\pi )=0,$ 등입니다. 오직 하나의 값이 희망될 때, 그 함수는 그것의 주요 가지(principal branch)로 제한될 수 있습니다. 이 제한과 함께, 모메인에서 각 $x$에 대해, 표현 $\arcsin (x)$은 그것의 주요 값(principal value)이라고 불리는 단일 값으로 오직 평가될 것입니다. 이들 속성은 모든 역 삼각 함수에 적용됩니다.

주요 역은 다음 테이블에 나열됩니다.

주목: 일부 저자는 아크시컨트의 치역을 $(0\le y<\frac{\pi }{2}\text{ or }\pi \le y<\frac{3\pi }{2})$으로 정의하는데, 왜냐하면 탄젠트 함수는 이 도메인 위에 비-음수이기 때문입니다. 이것은 일부 계산을 보다 일관되게 만듭니다. 예를 들어, 이 치역을 사용하여, $\tan (\text{arcsec}(x))=\sqrt{x^2-1}$이지만, 치역 $(0\le y<\frac{\pi }{2}\text{ or }\frac{\pi }{2}<y\le \pi )$과 함께, 우리는 $\tan (\text{arcsec}(x))=\pm \sqrt{x^2-1}$를 쓰야할 것인데, 왜냐하면 탄젠트는 $0\le y<\frac{\pi }{2}$에서 비-음수이지만, $\frac{\pi }{2}<y\le \pi$에서 비-양수이기 때문입니다. 유사한 이유로, 같은 저자는 아크코시컨트의 치역을 $(-\pi <y\le -\frac{\pi }{2}$ or $0<y\le \frac{\pi }{2})$으로 정의합니다.

만약 $x$가 복소수(complex number)이도록 허용되면, $y$의 치역은 오직 그것의 실수 부분에 적용됩니다.

아래 테이블은 역삼각 함수의 이름과 도메인을 라디안(radians)에서 보통의 주요 값(principal value)의 치역(range)과 함께 표시합니다.

기호 ${\displaystyle \mathbb{R}=(-\mathrm{\infty },\mathrm{\infty })}$는 모든 실수(real number)의 집합을 나타내고 ${\displaystyle \mathbb{Z}=\{\dots ,-2,-1,0,1,2,\dots \}}$는 모든 정수(integer)의 집합을 나타냅니다. ${\displaystyle \pi }$의 모든 정수 배수의 집합은 다음에 의해 표시됩니다:

${\displaystyle \pi \mathbb{Z}:=\{\pi n:n\in \mathbb{Z}\}=\{\dots ,-3\pi -2\pi ,-\pi ,0,\pi ,2\pi ,3\pi ,4\pi ,\dots \}=\{\theta \in \mathbb{R}:\sin \theta =0\}.}$

기호 ${\displaystyle \setminus }$는, 예를 들어, ${\displaystyle \mathbb{R}\setminus (-1,1)}$은 이 경우에서 두 구간 ${\displaystyle (-\mathrm{\infty },-1]\cup [1,\mathrm{\infty })}$에서 모든 점의 집합과 같은 구간 ${\displaystyle (-1,1)}$에 있지 않은 ${\displaystyle \mathbb{R}}$ (즉, 실수)에서 점의 집합이 되도록 집합 뺄셈(set subtraction)을 나타냅니다. 유사하게, ${\displaystyle [0,\pi ]\setminus \left\{\frac{\pi }{2}\right\}}$는 ${\displaystyle \frac{\pi }{2}}$와 같지 않은 구간  ${\displaystyle [0,\pi ]}$에서 모든 점의 집합이고 반면에 ${\displaystyle [-\frac{\pi }{2},\frac{\pi }{2}]\setminus \{0\}}$는 다음으로 구간의 관점에서 쓰여질 수 있는 ${\displaystyle 0}$와 같지 않은 ${\displaystyle [-\frac{\pi }{2},\frac{\pi }{2}]}$에서 모든 점의 집합입니다. 

${\displaystyle [-\frac{\pi }{2},\frac{\pi }{2}]\setminus \{0\}=[-\frac{\pi }{2},0)\cup (0,\frac{\pi }{2}]\text{ and }[0,\pi ]\setminus \left\{\frac{\pi }{2}\right\}=[0,\frac{\pi }{2})\cup (\frac{\pi }{2},\pi ].}$

${\displaystyle \cot ,\csc ,\tan }$, 및 ${\displaystyle \sec }$의 도메인을 간결하게 쓰기 위해 위에서 사용된 민코프스키 합(Minkowski sum) 표기법 ${\displaystyle \pi \mathbb{Z}+(0,\pi )}$와 ${\displaystyle \pi \mathbb{Z}+(-\frac{\pi }{2},\frac{\pi }{2})}$은 이제 설명됩니다.

코탄젠트 ${\displaystyle \cot }$와 코시컨트 ${\displaystyle \csc }$의 도메인: 
${\displaystyle \cot }$와 ${\displaystyle \csc }$의 도메인은 같습니다. 그것들은 ${\displaystyle \sin \theta \ne 0}$에서 모든 각도 ${\displaystyle \theta }$의 집합이며, 역시 다음으로 쓰여질 수 있습니다:

${\displaystyle \begin{array}{rl}\pi \mathbb{Z}+(0,\pi )& =\cdots \cup (-3\pi ,-2\pi )\cup (-2\pi ,-\pi )\cup (-\pi ,0)\cup (0,\pi )\cup (\pi ,2\pi )\cup (2\pi ,3\pi )\cup (3\pi ,4\pi )\cup \cdots \\ & =\mathbb{R}\setminus \pi \mathbb{Z}.\end{array}}$

다시 말해서, ${\displaystyle \cot }$, 및 ${\displaystyle \csc }$의 도메인은 일부 정수 ${\displaystyle n}$에 대해 형식 ${\displaystyle \pi n}$의 것이 아닌 모든 실수의 집합 ${\displaystyle \mathbb{R}\setminus \pi \mathbb{Z}}$입니다. 
도메인에 있지 않는 이들 점 (정수 ${\displaystyle n}$에 대해 ${\displaystyle \pi n}$를 의미함)은 ${\displaystyle 0=\sin \theta }$에서 정확하게 그들 숫자 ${\displaystyle \theta }$입니다; 이것은 이것들이 역시 ${\displaystyle \cot \theta =\frac{\cos \theta }{\sin \theta }}$와 ${\displaystyle \csc \theta =\frac{1}{\sin \theta }}$가 ${\displaystyle 0}$에 의해 나뉘어질 수 있는 것에서 정확하게 ${\displaystyle \theta }$이기 때문입니다. 

탄젠트 ${\displaystyle \tan }$와 시컨트 ${\displaystyle \sec }$의 도메인: 
${\displaystyle \tan }$와 ${\displaystyle \sec }$의 도메인은 같습니다. 그것들은 ${\displaystyle \cos \theta \ne 0}$에서 모든 각도 ${\displaystyle \theta }$의 집합이며, 역시 다음으로 쓰여질 수 있습니다:

${\displaystyle \begin{array}{rl}\pi \mathbb{Z}+(-\frac{\pi }{2},\frac{\pi }{2})& =\cdots \cup (-\frac{5\pi }{2},-\frac{3\pi }{2})\cup (-\frac{3\pi }{2},-\frac{\pi }{2})\cup (-\frac{\pi }{2},\frac{\pi }{2})\cup (\frac{\pi }{2},\frac{3\pi }{2})\cup (\frac{3\pi }{2},\frac{5\pi }{2})\cup (\frac{5\pi }{2},\frac{7\pi }{2})\cup \cdots \\ & =\mathbb{R}\setminus (\frac{\pi }{2}+\pi \mathbb{Z})\end{array}}$

여기서 ${\displaystyle \mathbb{R}\setminus (\frac{\pi }{2}+\pi \mathbb{Z})}$은 다음 집합에 속하지 않는 모든 실수의 집합입니다:

${\displaystyle \begin{array}{rl}\frac{\pi }{2}+\pi \mathbb{Z}:& =\{\frac{\pi }{2}+\pi n:n\in \mathbb{Z}\}\\ & =\{\dots ,\frac{\pi }{2}-3\pi ,\frac{\pi }{2}-2\pi ,\frac{\pi }{2}-\pi ,\frac{\pi }{2},\frac{\pi }{2}+\pi ,\frac{\pi }{2}+2\pi ,\frac{\pi }{2}+3\pi ,\dots \}\\ & =\{\dots ,-\frac{5\pi }{2},-\frac{3\pi }{2},-\frac{\pi }{2},\frac{\pi }{2},\frac{3\pi }{2},\frac{5\pi }{2},\frac{7\pi }{2},\dots \}\\ & =\{\theta \in \mathbb{R}:\cos \theta =0\}.\end{array}}$

다시 말해서, ${\displaystyle \tan }$와 ${\displaystyle \sec }$의 도메인은 일부 정수 ${\displaystyle n}$에 대해 형식 ${\displaystyle \frac{\pi }{2}+\pi n=\frac{\pi +2\pi n}{2}=\frac{\pi (1+2n)}{2}}$의 것이 아닌 모든 실수의 집합입니다; 이것은 역시 일부 홀수 정수 ${\displaystyle o}$에 대해 형식 ${\displaystyle \frac{o}{2}\pi }$의 것이 아닌 모든 실수의 집합입니다. 도메인에 있지 않은 이들 점 (정수 ${\displaystyle n}$에 대해 ${\displaystyle \frac{\pi }{2}+\pi n}$를 의미함)은 ${\displaystyle 0=\cos \theta }$에서 정확하게 그것들 숫자 ${\displaystyle \theta }$입니다; 이것은 이것들이 역시 ${\displaystyle \tan \theta =\frac{\sin \theta }{\cos \theta }}$와 ${\displaystyle \sec \theta =\frac{1}{\cos \theta }}$가 ${\displaystyle 0}$에 의해 나뉘어질 수 있는 것에서 정확하게 ${\displaystyle \theta }$이기 때문입니다.

Solutions to elementary trigonometric equations

각 삼각 함수는 그것의 인수의 실수 부분에서 주기적이며, $2\pi$의 각 구간에서 모든 그것의 값을 통해 두 번 실행합니다:

• 사인과 코시컨트는 $2\pi k-\frac{\pi }{2}$에서 그것들의 주기를 시작하고 (여기서 $k$는 정수),  $2\pi k+\frac{\pi }{2}$에서 주기를 끝내고, 그런-다음 $2\pi k+\frac{\pi }{2}$에서 $2\pi k+\frac{3\pi }{2}$에 걸쳐 자체를 역전합니다. 
• 코사인과 시컨트는 $2\pi k$에서 그것들의 주기를 시작하고, $2\pi k+\pi .$에서 주기를 끝내고 그런-다음 $2\pi k+\pi$에서 $2\pi k+2\pi$에 걸쳐 자체를 역전합니다. 
• 탄젠트는 $2\pi k-\frac{\pi }{2}$에서 그것의 주기를 시작하고, $2\pi k+\frac{\pi }{2}$에서 주기를 끝내고, 그런-다음 $2\pi k+\frac{\pi }{2}$에서 $2\pi k+\frac{3\pi }{2}$에 걸쳐 (전방으로) 그것을 반복합니다. 
• 코탄젠트는 $2\pi k$에서 그것의 주기를 시작하고, $2\pi k+\pi ,$에서 그것을 끝내고, 그런-다음 $2\pi k+\pi$에서 $2\pi k+2\pi$에 걸쳐 (전방으로) 그것을 반복합니다.

이 주기성은 $k$가 정수인 곳에서 일반저인 역에 반영됩니다.

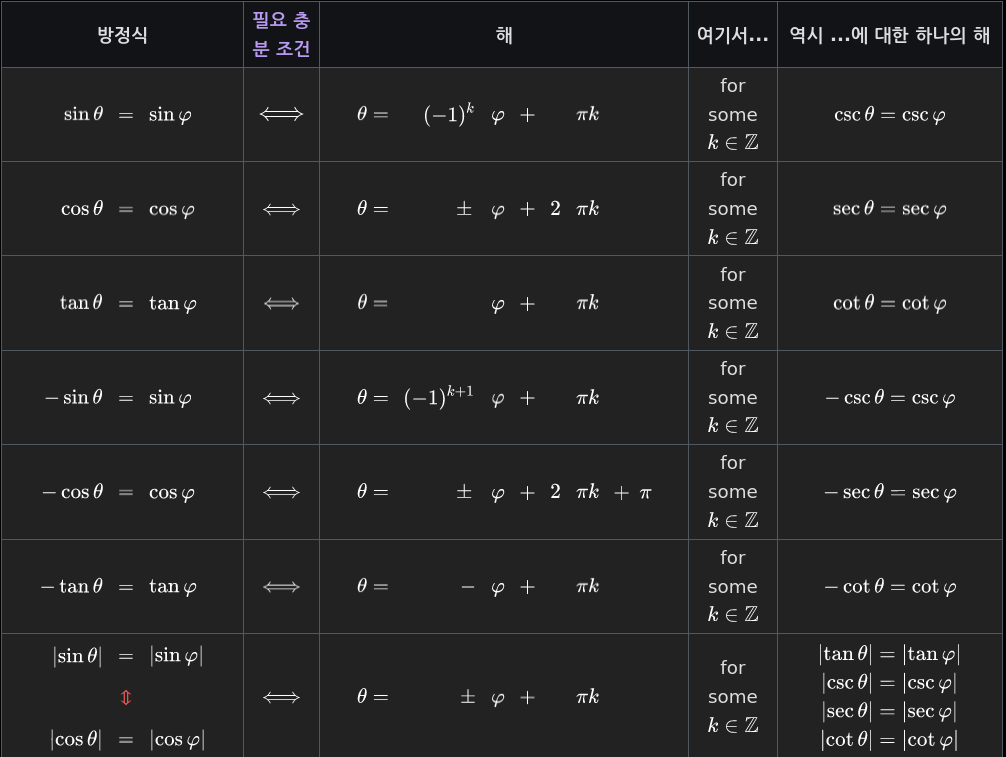
다음 테이블은 역 삼각 함수가 여섯 표준 삼각 함수와 관련된 상등을 풀기 위해 사용될 수 있는 방법을 보여줍니다.
주어진 값 $\theta ,$ $r,$ $s,$ $x,$ 및 $y$ 모두가 아래 관련된 표현이 잘-정의(well-defined)되도록 적절한 치역 내에 놓임을 가정합니다. "일부 $k\in \mathbb{Z}$에 대해"는 단지 "일부 정수 $k$에 대해"를 말하는 또 다른 방법임을 주목하십시오.

기호 $⟺$는 논리적으로 상등(logical equality)입니다.  표현 "왼쪽 변 $⟺$ 오른쪽 변"은 (a) 왼쪽 변과 오른쪽 변이 둘 다 참이거나, 그렇지 않으면 (b) 왼쪽 변과 오른쪽 변이 둘 다 거짓이라는 것 중에 하나임을 나타냅니다; 다른 선택이 없습니다 (c) (에를 들어, 왼쪽 변 명제에 대해 참이 되고 역시 동시에 오른쪽 명제에 대해 거짓이 되는 것은 가능하지 않습니다), 왜냐하면 그렇지 않으면 "왼쪽 변 $⟺$ 오른쪽 변"은 잘못 쓰인 것이기 때문입니다 (이 개념을 묘사하는 예제에 대해 이 각주를 참조하십시오).

예를 들어, 만약 $\cos \theta =-1$이면 일부 $k\in \mathbb{Z}$에 대해 $\theta =\pi +2\pi k=-\pi +2\pi (1+k)$입니다. 반면에 만약 $\sin \theta =\pm 1$이면 일부 $k\in \mathbb{Z}$에 대해 $\theta =\frac{\pi }{2}+\pi k=-\frac{\pi }{2}+\pi (k+1)$이며, 여기서 $k$는 $\sin \theta =1$이면 짝수일 것이고 $\sin \theta =-1$이면 홀수일 것입니다. 방정식 $\sec \theta =-1$와 $\csc \theta =\pm 1$는 각각 $\cos \theta =-1$와 $\sin \theta =\pm 1$와 같은 해를 가집니다. 방금 풀린 것을 제외 (즉, $\sin$/$\csc \theta =\pm 1$와 $\cos$/$\sec \theta =-1$를 제외)하고 위의 모든 방정식에서, 해의 공식에서 정수 $k$는 (고정된 $r,s,x,$ 및 $y$에 대해) $\theta$에 의해 고유하게 결정됩니다.

 

"더하기 또는 빼기" 기호 $\pm$의 자세한 예제와 설명

$\cos \theta =x$와 $\sec \theta =x$에 대한 해는 이제 "더하기 또는 빼기" 기호 $\pm$를 포함하고, 그것의 의미는 이제 명확해집니다. 오직 $\cos \theta =x$에 대한 해가 논의될 것인데 왜냐하면  $\sec \theta =x$에 대한 논의가 같기 때문입니다.
우리는 $-1\le x\le 1$ 사이의 $x$가 주어지고 우리는 $\cos \theta =x$를 만족시키는 일부 주어진 구간에서 각도 $\theta$가 있음을 압니다. 우리는 이 $\theta$를 찾기를 원합니다. 해에 대해 공식은 다음을 포함합니다:
$\pm \arccos x.$ 

만약 $\arccos x=0$ (이것은 오직 $x=1$일 때 발생), $+\arccos x=0$와 $-\arccos x=0$이므로 두 방법, $\pm \arccos x$은 $0$과 오직 같을 수 있습니다. 그러나 만약 $\arccos x\ne 0$이면, 이것이 가정되는 것이며,  $\cos \theta =x$에 대한 해는, 위에서 다음으로 쓰인 것처럼,  
$\theta =\pm \arccos x+2\pi k\text{ for some }k\in \mathbb{Z}$

다음 명제로 축약됩니다:

어느 쪽도

• $\theta =\arccos x+2\pi k$ for some integer $k,$
• 또는 그렇지 않으면 
• $\theta =-\arccos x+2\pi k$ for some integer $k.$

$\arccos x\ne 0$와 $0<\arccos x\le \pi$이기 때문에, 이들 두 방정식 중 정확하게 하나가 유지될 수 있습니다. $\theta$에 대한 추가적인 정보는 어느 하나가 유지되는지 결정하기 위해 필요됩니다. 예를 들어, $x=0$이고 $\theta$에 대한 알려진 모두가 $-\pi \le \theta \le \pi$임을 가정합니다 (그리고 더 이상 알려진 것이 없습니다). 그런-다음

$\arccos x=\arccos 0=\frac{\pi }{2}$ 

그리고 게다가, 이 특정 경우에서 $k=0$ ($+$ 경우와 $-$ 경우 둘 다에 대해)이고 따라서 결론적으로,

${\displaystyle \theta =\pm \arccos x+2\pi k=\pm \left(\frac{\pi }{2}\right)+2\pi (0)=\pm \frac{\pi }{2}.}$

이것은 $\theta$가 $\pi /2$ or $-\pi /2$ 중 하나일 수 있음을 의미합니다. 추가적인 정보없이, $\theta$가 가지는 이들 값의 어떤 것을 결정하는 것은 가능하지 않습니다. $\theta$의 값을 결정할 수 있는 일부 추가적인 정보의 예제는 그 각도가 $x$-축 위에 있음을 알거나 (이 경우에서 $\theta =\pi /2$) 대안적으로, 그것이 $x$-축 아래에 있는 것을 아는 것입니다 (이 경우에서 $\theta =-\pi /2$).

방정식 변환하기

위의 방정식은 반사와 이동 항등식을 사용함으로써 변환될 수 있습니다:

이들 공식은, 특히, 다음이 유지됨을 의미합니다:

$\begin{array}{rlrlrlrlrlrlrlrlrlrlrlrlrlrlrlrlrlrl}\sin \theta & =-& & \sin (-\theta )& & =-& & \sin (\pi +\theta )& & =& & \sin (\pi -\theta )& & =-& & \cos (\frac{\pi }{2}+\theta )& & =& & \cos (\frac{\pi }{2}-\theta )& & =-& & \cos (-\frac{\pi }{2}-\theta )& & =& & \cos (-\frac{\pi }{2}+\theta )& & =-& & \cos (\frac{3\pi }{2}-\theta )& & =-& & \cos (-\frac{3\pi }{2}+\theta )\\ \cos \theta & =& & \cos (-\theta )& & =-& & \cos (\pi +\theta )& & =& & \cos (\pi -\theta )& & =& & \sin (\frac{\pi }{2}+\theta )& & =& & \sin (\frac{\pi }{2}-\theta )& & =-& & \sin (-\frac{\pi }{2}-\theta )& & =-& & \sin (-\frac{\pi }{2}+\theta )& & =-& & \sin (\frac{3\pi }{2}-\theta )& & =& & \sin (-\frac{3\pi }{2}+\theta )\\ \tan \theta & =-& & \tan (-\theta )& & =& & \tan (\pi +\theta )& & =-& & \tan (\pi -\theta )& & =-& & \cot (\frac{\pi }{2}+\theta )& & =& & \cot (\frac{\pi }{2}-\theta )& & =& & \cot (-\frac{\pi }{2}-\theta )& & =-& & \cot (-\frac{\pi }{2}+\theta )& & =& & \cot (\frac{3\pi }{2}-\theta )& & =-& & \cot (-\frac{3\pi }{2}+\theta )\end{array}$
여기서 $\sin \leftrightarrow \csc$를 서로 바꾸고, $\cos \leftrightarrow \sec$를 서로 바꾸고, $\tan \leftrightarrow \cot$를 서로 바꾸면 각각 $\csc ,\sec$, 및 $\cot$에 대해 유사한 방정식을 제고합니다.

따라서 예를 들어, 상등 $\sin (\frac{\pi }{2}-\theta )=\cos \theta$을 사용함으로써, 방정식 $\cos \theta =x$은 $\sin (\frac{\pi }{2}-\theta )=x$로 변환될 수 있으며, 해에 대해 사용되려는 방정식 $\sin \phi =x$ (여기서 $\phi :=\frac{\pi }{2}-\theta$)을 허용합니다; 그 해는 다음입니다: $\phi =(-1{)}^k\arcsin (x)+\pi k\text{ for some }k\in \mathbb{Z},$ 이것은 다음이 됩니다:

${\displaystyle \frac{\pi }{2}-\theta =(-1{)}^k\arcsin (x)+\pi k\text{ for some }k\in \mathbb{Z}}$

여기서 $(-1{)}^k=(-1{)}^{-k}$이라는 사실을 사용하고 $h:=-k$를 치환하면 $\cos \theta =x$에 대한 또 다른 해가 다음임을 입증합니다:

${\displaystyle \theta =(-1{)}^{h+1}\arcsin (x)+\pi h+\frac{\pi }{2}\text{ for some }h\in \mathbb{Z}.}$

치환 $\arcsin x=\frac{\pi }{2}-\arccos x$은 $\arcsin x$ 대신에 $\arccos x$의 관점에서 위의 공식의 오른쪽 변을 표현하기 위해 사용될 수 있습니다.

Equal identical trigonometric functions

Equal identical trigonometric functions

아래 테이블은 두 각도 $\theta$와 $\phi$가 만약 주어진 삼각 함수 아래에서 그것들의 값이 서로 같거나 음수이면 관련되어야 하는 방법을 보여줍니다.

Relationships between trigonometric functions and inverse trigonometric functions

역 삼각 함수의 삼각 함수는 아래 테이블에 정리되어 있습니다. 그것들을 유도하기 위한 빠른 방법은 길이 1의 한 변과 또 다른 변의 길이 $x$를 갖는 직각 삼각형의 기하학을 고려하고, 그런-다음 피타고라스 정리(Pythagorean theorem)와 삼각 비율의 정의를 적용하는 것입니다. 순수하게 대수적 유도는 더 깁니다. 아크코시컨트와 아크코시컨트에 대해, 다이어그램은 $x$가 양수라고 가정하고 따라서 그 결과는 절댓값(absolute value)과 시그넘(signum)(sgn) 연산의 사용을 통해 수정되어야 함을 주목할 가치가 있습니다.

Relationships among the inverse trigonometric functions

보충 각도:

$\begin{array}{rl}\arccos (x)& =\frac{\pi }{2}-\arcsin (x)\\ \text{arccot}(x)& =\frac{\pi }{2}-\arctan (x)\\ \text{arccsc}(x)& =\frac{\pi }{2}-\text{arcsec}(x)\end{array}$

음의 인수:

$\begin{array}{rl}\arcsin (-x)& =-\arcsin (x)\\ \arccos (-x)& =\pi -\arccos (x)\\ \arctan (-x)& =-\arctan (x)\\ \text{arccot}(-x)& =\pi -\text{arccot}(x)\\ \text{arcsec}(-x)& =\pi -\text{arcsec}(x)\\ \text{arccsc}(-x)& =-\text{arccsc}(x)\end{array}$

역수 인수:

$\begin{array}{rl}\arccos \left(\frac{1}{x}\right)& =\text{arcsec}(x)\\ \arcsin \left(\frac{1}{x}\right)& =\text{arccsc}(x)\\ \arctan \left(\frac{1}{x}\right)& =\frac{\pi }{2}-\arctan (x)=\text{arccot}(x),\text{ if }x>0\\ \arctan \left(\frac{1}{x}\right)& =-\frac{\pi }{2}-\arctan (x)=\text{arccot}(x)-\pi ,\text{ if }x<0\\ \text{arccot}\left(\frac{1}{x}\right)& =\frac{\pi }{2}-\text{arccot}(x)=\arctan (x),\text{ if }x>0\\ \text{arccot}\left(\frac{1}{x}\right)& =\frac{3\pi }{2}-\text{arccot}(x)=\pi +\arctan (x),\text{ if }x<0\\ \text{arcsec}\left(\frac{1}{x}\right)& =\arccos (x)\\ \text{arccsc}\left(\frac{1}{x}\right)& =\arcsin (x)\end{array}$

만약 하나가 오직 사인 테이블의 조각을 가지면 유용한 항등식:

$\begin{array}{rl}\arccos (x)& =\arcsin \left(\sqrt{1-x^2}\right),\text{ if }0\le x\le 1\text{ , from which you get }\\ \arccos & \left(\frac{1-x^2}{1+x^2}\right)=\arcsin \left(\frac{2x}{1+x^2}\right),\text{ if }0\le x\le 1\\ \arcsin & \left(\sqrt{1-x^2}\right)=\frac{\pi }{2}-\text{sgn}(x)\arcsin (x)\\ \arccos (x)& =\frac{1}{2}\arccos (2x^2-1),\text{ if }0\le x\le 1\\ \arcsin (x)& =\frac{1}{2}\arccos (1-2x^2),\text{ if }0\le x\le 1\\ \arcsin (x)& =\arctan \left(\frac{x}{\sqrt{1-x^2}}\right)\\ \arccos (x)& =\arctan \left(\frac{\sqrt{1-x^2}}{x}\right)\\ \arctan (x)& =\arcsin \left(\frac{x}{\sqrt{1+x^2}}\right)\\ \text{arccot}(x)& =\arccos \left(\frac{x}{\sqrt{1+x^2}}\right)\end{array}$

복소수의 제곱근이 여기에서 사용될 때마다, 우리는 양의 실수 부분 (또는 만약 제곱이 음의 실수이면 양의 허수 부분)을 갖는 근을 선택합니다.

위의 테이블에서 바로 뒤따르는 유용한 형식은 다음과 같습니다:

$\arctan \left(x\right)=\arccos \left(\sqrt{\frac{1}{1+x^2}}\right),\text{ if }x\ge 0$.

그것은 $\cos (\arctan \left(x\right))=\sqrt{\frac{1}{1+x^2}}=\cos (\arccos \left(\sqrt{\frac{1}{1+x^2}}\right))$을 인식함으로써 얻어집니다.

절반-각도 공식(half-angle formula), $\tan \left(\frac{\theta }{2}\right)=\frac{\sin (\theta )}{1+\cos (\theta )}$에서, 다음을 얻습니다:

$\begin{array}{rl}\arcsin (x)& =2\arctan \left(\frac{x}{1+\sqrt{1-x^2}}\right)\\ \arccos (x)& =2\arctan \left(\frac{\sqrt{1-x^2}}{1+x}\right),\text{ if }-1<x\le 1\\ \arctan (x)& =2\arctan \left(\frac{x}{1+\sqrt{1+x^2}}\right)\end{array}$

Arctangent addition formula

$\arctan (u)\pm \arctan (v)=\arctan \left(\frac{u\pm v}{1\mp uv}\right)(\mathrm{mod}\pi ),uv\ne 1.$

이것은 탄젠트 덧셈 공식(addition formula)에서 다음을 설정함으로써,

$\alpha =\arctan (u),\beta =\arctan (v)$

다음이 유도됩니다:

${\displaystyle \tan (\alpha \pm \beta )=\frac{\tan (\alpha )\pm \tan (\beta )}{1\mp \tan (\alpha )\tan (\beta )}.}$

In calculus

Derivatives of inverse trigonometric functions

z의 복소수 값에 대해 도함수(derivative)는 다음과 같습니다:

$\begin{array}{rlrl}\frac{d}{dz}\arcsin (z)& =\frac{1}{\sqrt{1-z^2}};& z& \ne -1,+1\\ \frac{d}{dz}\arccos (z)& =-\frac{1}{\sqrt{1-z^2}};& z& \ne -1,+1\\ \frac{d}{dz}\arctan (z)& =\frac{1}{1+z^2};& z& \ne -i,+i\\ \frac{d}{dz}\text{arccot}(z)& =-\frac{1}{1+z^2};& z& \ne -i,+i\\ \frac{d}{dz}\text{arcsec}(z)& =\frac{1}{z^2\sqrt{1-\frac{1}{z^2}}};& z& \ne -1,0,+1\\ \frac{d}{dz}\text{arccsc}(z)& =-\frac{1}{z^2\sqrt{1-\frac{1}{z^2}}};& z& \ne -1,0,+1\end{array}$

오직 x의 실수 값에 대해:

$\begin{array}{rlr}\frac{d}{dx}\text{arcsec}(x)& =\frac{1}{|x|\sqrt{x^2-1}};& |x|>1\\ \frac{d}{dx}\text{arccsc}(x)& =-\frac{1}{|x|\sqrt{x^2-1}};& |x|>1\end{array}$

견본 도함수에 대해: 만약 $\theta =\arcsin (x)$이면, 다음을 얻습니다:

${\displaystyle \frac{d\arcsin (x)}{dx}=\frac{d\theta }{d\sin (\theta )}=\frac{d\theta }{\cos (\theta )d\theta }=\frac{1}{\cos (\theta )}=\frac{1}{\sqrt{1-{\sin }^2(\theta )}}=\frac{1}{\sqrt{1-x^2}}}$

Expression as definite integrals

도함수를 적분하고 값을 한 점에 고정하면 역 삼각 함수에 대해 표현을 정적분으로 제공합니다:

$\begin{array}{rlrl}\arcsin (x)& ={\int }_0^x\frac{1}{\sqrt{1-z^2}}dz,& |x|& \le 1\\ \arccos (x)& ={\int }_x^1\frac{1}{\sqrt{1-z^2}}dz,& |x|& \le 1\\ \arctan (x)& ={\int }_0^x\frac{1}{z^2+1}dz,\\ \text{arccot}(x)& ={\int }_x^{\mathrm{\infty }}\frac{1}{z^2+1}dz,\\ \text{arcsec}(x)& ={\int }_1^x\frac{1}{z\sqrt{z^2-1}}dz=\pi +{\int }_{-x}^{-1}\frac{1}{z\sqrt{z^2-1}}dz,& x& \ge 1\\ \text{arccsc}(x)& ={\int }_x^{\mathrm{\infty }}\frac{1}{z\sqrt{z^2-1}}dz={\int }_{-\mathrm{\infty }}^{-x}\frac{1}{z\sqrt{z^2-1}}dz,& x& \ge 1\end{array}$

x가 1과 같을 때, 제한된 도메인을 갖는 적분은 부적절한 적분(improper integral)이지만, 여전히 잘-정의된 것입니다.

Infinite series

사인과 코사인 함수와 유사하게, 역 삼각 함수는 역시 다음처럼 거듭제곱 급수(power series)를 사용하여 계산될 수 있습니다. 아크사인에 대해, 그 급수는 그것의 도함수, $\frac{1}{\sqrt{1-z^2}}$를 이항 급수(binomial series)로 전개하고, (위에서 처럼 적분 정의를 사용하여) 항별로 적분함으로써 유도될 수 있습니다. 아크탄젠트에 대해 급수는 그것의 도함수 $\frac{1}{1+z^2}$를 기하 급수(geometric series)에서 전개하고, 위의 적분 정의를 적용함으로써 유사하게 유도될 수 있습니다 (라이프니츠 급수(Leibniz series)를 참조하십시오).

$\begin{array}{rl}\arcsin (z)& =z+\left(\frac{1}{2}\right)\frac{z^3}{3}+\left(\frac{1\cdot 3}{2\cdot 4}\right)\frac{z^5}{5}+\left(\frac{1\cdot 3\cdot 5}{2\cdot 4\cdot 6}\right)\frac{z^7}{7}+\cdots \\ & =\sum _{n=0}^{\mathrm{\infty }}\frac{(2n-1)!!}{(2n)!!}\frac{z^{2n+1}}{2n+1}\\ & =\sum _{n=0}^{\mathrm{\infty }}\frac{(2n)!}{(2^{n}n!{)}^2}\frac{z^{2n+1}}{2n+1};|z|\le 1\end{array}$

$\arctan (z)=z-\frac{z^3}{3}+\frac{z^5}{5}-\frac{z^7}{7}+\cdots =\sum _{n=0}^{\mathrm{\infty }}\frac{(-1{)}^n{z}^{2n+1}}{2n+1};|z|\le 1z\ne i,-i$

다른 역 삼각 함수에 대해 급수는 위에 주어진 관계에 따라 이들의 관점에서 제공될 수 있습니다. 예를 들어, $\arccos (x)=\pi /2-\arcsin (x)$, $\text{arccsc}(x)=\arcsin (1/x)$, 이런 식으로 계속됩니다. 또 다른 급수는 다음에 의해 제공됩니다:

${\displaystyle 2{(\arcsin \left(\frac{x}{2}\right))}^2=\sum _{n=1}^{\mathrm{\infty }}\frac{x^{2n}}{n^2(\genfrac{}{}{0ex}{}{2n}{n})}.}$

레온하르트 오일러(Leonhard Euler)는 그것의 테일러 급수(Taylor series)보다 더 빠르게 수렴하는 아크탄젠트에 대해 급수를 발견했습니다:

${\displaystyle \arctan (z)=\frac{z}{1+z^2}\sum _{n=0}^{\mathrm{\infty }}\prod _{k=1}^n\frac{2k{z}^2}{(2k+1)(1+z^2)}.}$

((합에서 n = 0에 대해 항은 빈 곱(empty product)이므로, 1입니다.)

대안적으로, 이것은 다음으로 표현될 수 있습니다:

${\displaystyle \arctan (z)=\sum _{n=0}^{\mathrm{\infty }}\frac{2^{2n}(n!{)}^2}{(2n+1)!}\frac{z^{2n+1}}{(1+z^2{)}^{n+1}}.}$

아크탄젠트 함수에 대해 또 다른 급수는 다음에 의해 제공됩니다:

${\displaystyle \arctan (z)=i\sum _{n=1}^{\mathrm{\infty }}\frac{1}{2n-1}(\frac{1}{(1+2i/z{)}^{2n-1}}-\frac{1}{(1-2i/z{)}^{2n-1}}),}$

여기서 $i=\sqrt{-1}$는 허수 단위(imaginary unit)입니다.

Continued fractions for arctangent

아크탄젠트에 대해 거듭제곱 급수에 대한 두 가지 대안은 다음과 같은 이들 일반화된 연속된 분수(generalized continued fraction)입니다:

$\arctan (z)=\frac{z}{1+\frac{(1z{)}^2}{3-1z^2+\frac{(3z{)}^2}{5-3z^2+\frac{(5z{)}^2}{7-5z^2+\frac{(7z{)}^2}{9-7z^2+\ddots }}}}}=\frac{z}{1+\frac{(1z{)}^2}{3+\frac{(2z{)}^2}{5+\frac{(3z{)}^2}{7+\frac{(4z{)}^2}{9+\ddots }}}}}$

이것들 중 두 번째는 절단된 복소 평면에서 유효합니다. −i에서 무한대에서 점까지 허수 축을 따라 내려가는 자름과 i에서 무한대에서 점까지 같은 축을 따라 올라가는 둘의 자름이 있습니다. 그것은 −1에서 1까지 실행하는 실수에 대해 가장 잘 작동합니다. 부분 분모는 홀수 자연수이고, 부분 분자 (첫 번째 뒤)는 단지 $(nz{)}^2$이며, 각 완전 제곱은 한 번 나타납니다. 첫 번째는 레온하르트 오일러(Leonhard Euler)에 의해 개발되었습니다; 두 번째는 가우스 초월기하 급수(Gaussian hypergeometric series)를 활용하는 카를 프리드리히 가우스(Carl Friedrich Gauss)에 의한 것입니다.

Indefinite integrals of inverse trigonometric functions

z의 실수와 복소수 값에 대해:

$\begin{array}{rl}\int \arcsin (z)dz& =z\arcsin (z)+\sqrt{1-z^2}+C\\ \int \arccos (z)dz& =z\arccos (z)-\sqrt{1-z^2}+C\\ \int \arctan (z)dz& =z\arctan (z)-\frac{1}{2}\ln (1+z^2)+C\\ \int \text{arccot}(z)dz& =z\text{arccot}(z)+\frac{1}{2}\ln (1+z^2)+C\\ \int \text{arcsec}(z)dz& =z\text{arcsec}(z)-\ln \left[z(1+\sqrt{\frac{z^2-1}{z^2}})\right]+C\\ \int \text{arccsc}(z)dz& =z\text{arccsc}(z)+\ln \left[z(1+\sqrt{\frac{z^2-1}{z^2}})\right]+C\end{array}$

실수 x ≥ 1에 대해:

$\begin{array}{rl}\int \text{arcsec}(x)dx& =x\text{arcsec}(x)-\ln (x+\sqrt{x^2-1})+C\\ \int \text{arccsc}(x)dx& =x\text{arccsc}(x)+\ln (x+\sqrt{x^2-1})+C\end{array}$

−1과 1 사이가 아닌 모든 실수 x에 대해:

$\begin{array}{rl}\int \text{arcsec}(x)dx& =x\text{arcsec}(x)-\text{sgn}(x)\ln \left(|x+\sqrt{x^2-1}|\right)+C\\ \int \text{arccsc}(x)dx& =x\text{arccsc}(x)+\text{sgn}(x)\ln \left(|x+\sqrt{x^2-1}|\right)+C\end{array}$

절댓값은 아크시컨트와 아크코시컨트 함수의 음수와 양수 값 둘 다에 대해 보상하기 위해 필요됩니다. 시그넘 함수는 역시 x의 양수와 음수 값에 대해 둘의 다른 해를 생성하는 두 함수의 도함수(derivative)에서 절댓값으로 인해 필요됩니다. 이것들은 역 쌍곡선 함수(inverse hyperbolic function)의 로그 정의를 사용하여 더 단순화될 수 있습니다:

$\begin{array}{rl}\int \text{arcsec}(x)dx& =x\text{arcsec}(x)-\mathrm{arcosh}(|x|)+C\\ \int \text{arccsc}(x)dx& =x\text{arccsc}(x)+\mathrm{arcosh}(|x|)+C\end{array}$

arcosh 함수의 인수에 있는 절댓값은 그것의 그래프의 음의 절반을 생성하여, 위에 표시된 시그넘 로그 함수와 동일하게 만듭니다.

모든 이들 역도함수는 위에 표시된 부분에 의한 적분(integration by parts)과 간단한 도함수 형식을 사용하여 유도될 수 있습니다.

Example

$\int udv=uv-\int vdu$ (즉, 부분에 의한 적분)을 사용하여, 다음을 설정합니다:

$\begin{array}{rlrl}u& =\arcsin (x)& dv& =dx\\ du& =\frac{dx}{\sqrt{1-x^2}}& v& =x\end{array}$

그런-다음

${\displaystyle \int \arcsin (x)dx=x\arcsin (x)-\int \frac{x}{\sqrt{1-x^2}}dx,}$

이것은 간단한 치환(substitution) $w=1-x^2,dw=-2xdx$에 의해 마지막 결과를 산출합니다:

${\displaystyle \int \arcsin (x)dx=x\arcsin (x)+\sqrt{1-x^2}+C}$

Extension to complex plane

역 삼각 함수는 해석적 함수(analytic function)이기 때문에, 그것들은 실수 직선에서 복소 평면으로 확장될 수 있습니다. 이것은 여러 판(sheet)과 가지 점(branch point)을 갖는 함수를 초래합니다. 확장을 정의하는 한 가지 가능한 방법은 다음과 같습니다:

${\displaystyle \arctan (z)={\int }_0^z\frac{dx}{1+x^2}z\ne -i,+i}$

여기서 가지 점 (−i와 +i) 사이에 엄격하게 놓이지 않는 허수 축의 부분은 주요 판과 다른 판 사이의 가지 절단(branch cut)입니다. 적분의 경로는 가지 절단을 가로지르지 않아야 합니다. 가지 절단 위가 아닌 z에 대해, 0에서 z까지의 직선 경로가 그러한 하나의 경로입니다. 가지 절단 위에 z에 대해, 그 경로는 위쪽 가지 절단에 대해 Re[x] > 0에서 및 아래쪽 가지 절단에 대해 Re[x] < 0에서 접근해야 합니다.

아크사인 함수는 그런-다음 다음처럼 정의될 수 있습니다:

${\displaystyle \arcsin (z)=\arctan \left(\frac{z}{\sqrt{1-z^2}}\right)z\ne -1,+1}$

여기서 (제곱근 함수는 음의 실수 축을 따라 그것의 절단을 가지고) −1과 +1 사이에 엄격하게 놓이지 않는 실수 축의 부분은 아크사인의 주요 판과 다른 판 사이의 가지 절단입니다;

${\displaystyle \arccos (z)=\frac{\pi }{2}-\arcsin (z)z\ne -1,+1}$

이것은 다음처럼 같은 절단을 가집니다;

${\displaystyle \text{arccot}(z)=\frac{\pi }{2}-\arctan (z)z\ne -i,i}$

이것은 아크탄젠트처럼 같은 절단을 가집니다;

${\displaystyle \text{arcsec}(z)=\arccos \left(\frac{1}{z}\right)z\ne -1,0,+1}$

여기서 –1과 +1 포함한 사이의 실수 축의 부분은 아크시컨트의 주요 판과 다른 판 사이의 절단입니다;

${\displaystyle \text{arccsc}(z)=\arcsin \left(\frac{1}{z}\right)z\ne -1,0,+1}$

이것은 아크시컨트와 같은 절단을 가집니다:

Logarithmic forms

이들 함수는 역시 복소 로그(complex logarithm)를 사용하여 표현될 수 있습니다. 이것은 자연스러운 방식에서 복소 평면(complex plane)으로 그것들 도메인(domains)을 확장합니다. 함수의 주요 값에 대해 다음 항등식은 그것들의 가지 자름에서도 정의된 모든 곳에서 유지됩니다.

$\begin{array}{rlr}\arcsin (z)& =-i\ln (\sqrt{1-z^2}+iz)=i\ln (\sqrt{1-z^2}-iz)& =\text{arccsc}\left(\frac{1}{z}\right)\\ \arccos (z)& =-i\ln (i\sqrt{1-z^2}+z)=\frac{\pi }{2}-\arcsin (z)& =\text{arcsec}\left(\frac{1}{z}\right)\\ \arctan (z)& =-\frac{i}{2}\ln \left(\frac{i-z}{i+z}\right)=-\frac{i}{2}\ln \left(\frac{1+iz}{1-iz}\right)& =\text{arccot}\left(\frac{1}{z}\right)\\ \text{arccot}(z)& =-\frac{i}{2}\ln \left(\frac{z+i}{z-i}\right)=-\frac{i}{2}\ln \left(\frac{iz-1}{iz+1}\right)& =\arctan \left(\frac{1}{z}\right)\\ \text{arcsec}(z)& =-i\ln (i\sqrt{1-\frac{1}{z^2}}+\frac{1}{z})=\frac{\pi }{2}-\text{arccsc}(z)& =\arccos \left(\frac{1}{z}\right)\\ \text{arccsc}(z)& =-i\ln (\sqrt{1-\frac{1}{z^2}}+\frac{i}{z})=i\ln (\sqrt{1-\frac{1}{z^2}}-\frac{i}{z})& =\arcsin \left(\frac{1}{z}\right)\end{array}$

Generalization

역 삼각 함수 모두는 직각삼각형의 각도를 출력하기 때문에, 그것들은 오일러의 공식(Euler's formula)을 사용함으로써 복소평면에서 직각 삼각형을 형성하기 위해 일반화될 수 있습니다. 대수적으로 이것은 우리에게 다음을 제공합니다. 대수적으로, 이것은 다음을 제공합니다:

$c{e}^{\theta i}=c\cos (\theta )+ci\sin (\theta )$

또는

${\displaystyle c{e}^{\theta i}=a+bi}$

여기서 $a$는 인접 변, $b$는 반대 각도이고, $c$는 빗변입니다. 여기에서, 우리는 $\theta$에 대해 풀 수 있습니다.

$\begin{array}{rl}{e}^{\ln (c)+\theta i}& =a+bi\\ \ln c+\theta i& =\ln (a+bi)\\ \theta & =\mathrm{Im}(\ln (a+bi))\end{array}$

또는

$\theta =-i\ln \left(\frac{a+bi}{c}\right)=i\ln \left(\frac{c}{a+bi}\right)$

단순히 허수 부분을 취하면 임의의 실수-값 $a$와 $b$에 대해 작동하지만, 만약 $a$ 또는 $b$가 복소-값이면, 우리는 결과의 실수 부분이 제외되지 않도록 최종 방정식을 사용해야 합니다. 빗변의 길이는 각도를 변경하지 않기 때문에, $\ln (a+bi)$의 실수 부분을 무시하면 역시 방정식에서 $c$를 제거합니다. 마지막 방정식에서, 우리는 복소 평면에서 삼각형의 각도가 각 변의 길이를 입력함으로써 찾아질 수 있음을 알고 있습니다. 세 변 중 하나를 1과 같게 설정하고 남아있는 변 중 하나를 입력 $z$와 같게 설정함으로써, 전체 여섯 방정식에 대해, 역 삼각 함수 중 하나에 대해 공식을 얻습니다. 역 삼각 함수는 오직 하나의 입력을 요구하기 때문에, 피타고라스 정리(Pythagorean Theorem) 관계를 사용하여 삼각형의 마지막 변을 나머지 두 변의 항에 넣어야 합니다:

$a^2+b^2=c^2$

아래 테이블은 각 역 삼각 함수에 대해, a, b, 및 c의 값과 위의 방정식에 값을 대입하고 단순화한 결과인 $\theta$에 대해 등가 표현식을 보여줍니다.

$\begin{array}{rlrlrlrlrlrl}& a& & b& & c& & \theta & & {\theta }_{\text{simplified}}& & {\theta }_{a,b\in \text{R}}\\ \arcsin (z)& \sqrt{1-z^2}& & z& & 1& & -i\ln \left(\frac{\sqrt{1-z^2}+zi}{1}\right)& & =-i\ln (\sqrt{1-z^2}+zi)& & \mathrm{Im}(\ln (\sqrt{1-z^2}+zi))\\ \arccos (z)& z& & \sqrt{1-z^2}& & 1& & -i\ln \left(\frac{z+i\sqrt{1-z^2}}{1}\right)& & =-i\ln (z+\sqrt{z^2-1})& & \mathrm{Im}(\ln (z+\sqrt{z^2-1}))\\ \arctan (z)& 1& & z& & \sqrt{1+z^2}& & i\ln \left(\frac{\sqrt{1+z^2}}{1+zi}\right)& & =\frac{i}{2}\ln \left(\frac{i+z}{i-z}\right)& & \mathrm{Im}(\ln (1+zi))\\ \text{arccot}(z)& z& & 1& & \sqrt{z^2+1}& & i\ln \left(\frac{\sqrt{z^2+1}}{z+i}\right)& & =\frac{i}{2}\ln \left(\frac{z-i}{z+i}\right)& & \mathrm{Im}(\ln (z+i))\\ \text{arcsec}(z)& 1& & \sqrt{z^2-1}& & z& & -i\ln \left(\frac{1+i\sqrt{z^2-1}}{z}\right)& & =-i\ln (\frac{1}{z}+\sqrt{\frac{1}{z^2}-1})& & \mathrm{Im}(\ln (1+\sqrt{1-z^2}))\\ \text{arccsc}(z)& \sqrt{z^2-1}& & 1& & z& & -i\ln \left(\frac{\sqrt{z^2-1}+i}{z}\right)& & =-i\ln (\sqrt{1-\frac{1}{z^2}}+\frac{i}{z})& & \mathrm{Im}(\ln (\sqrt{z^2-1}+i))\end{array}$

이런 의미에서, 모든 역 삼각 함수는 복소-값 로그 함수의 특정한 경우로 생각될 수 있습니다. 이 정의는 임의의 복소-값 $z$에 대해 작동하기 때문에, 이 정의는 쌍곡선 각도(hyperbolic angle)를 출력으로 허용하고 역 쌍곡선 함수(inverse hyperbolic functions)를 나아가서 정의하기 위해 사용될 수 있습니다. 관계의 기본 증명은 역시 삼각 함수의 지수 형식으로 확장을 통해 진행할 수 있습니다.

Example proof

$\begin{array}{rl}\sin (\varphi )& =z\\ \varphi & =\arcsin (z)\end{array}$

사인의 지수 정의(exponential definition of sine)를 사용하여, 다음을 얻습니다:

$\text{quadz}=\frac{e^{\varphi i}-e^{-\varphi i}}{2i}$

다음으로 놓습니다:

${\displaystyle \xi =e^{\varphi i}}$

$\varphi$에 대해 풀면

$\begin{array}{rl}z& =\frac{\xi -\frac{1}{\xi }}{2i}\\ 2iz& =\xi -\frac{1}{\xi }\\ \xi -2iz-\frac{1}{\xi }& =0\\ {\xi }^2-2i\xi z-1& =0\\ \xi & =iz\pm \sqrt{1-z^2}=e^{\varphi i}\\ \varphi i& =\ln (iz\pm \sqrt{1-z^2})\\ \varphi & =-i\ln (iz\pm \sqrt{1-z^2})\end{array}$

(양의 가지가 선택됩니다)

${\displaystyle \varphi =\arcsin (z)=-i\ln (iz+\sqrt{1-z^2})}$

Applications

Finding the angle of a right triangle

역 삼각 함수는 삼각형의 변의 길이가 알려져 있을 때 직각 삼각형(right triangle)의 남아있는 두 각도를 결정하려고 시도할 때 유용합니다. 사인과 코사인의 직각 삼각형 정의를 상기하면, 그것은 다음임을 따릅니다:

${\displaystyle \theta =\arcsin \left(\frac{\text{opposite}}{\text{hypotenuse}}\right)=\arccos \left(\frac{\text{adjacent}}{\text{hypotenuse}}\right).}$

종종, 빗변은 알려져 있지 않고 피타고라스 정리(Pythagorean Theorem): $a^2+b^2=h^2$를 사용하여 아크사인 또는 아크코사인을 사용하기 전에 계산되어야 합니다; 여기서 $h$는 빗변의 길이입니다. 아크탄젠트는 빗변의 길이가 필요하지 않기 때문에 이 상황에서 유용합니다.

${\displaystyle \theta =\arctan \left(\frac{\text{opposite}}{\text{adjacent}}\right).}$

예를 들어, 지붕이 20피트 밖으로 나가면서 8피트가 떨어진다고 가정합니다. 지붕은 수평과 각도 θ를 만들며, 여기서 θ는 다음과 같이 계산될 수 있습니다:

${\displaystyle \theta =\arctan \left(\frac{\text{opposite}}{\text{adjacent}}\right)=\arctan \left(\frac{\text{rise}}{\text{run}}\right)=\arctan \left(\frac{8}{20}\right)\approx {21.8}^{\circ }.}$

In computer science and engineering

Two-argument variant of arctangent

둘의 인수를 갖는 atan2 함수는 y와 x가 주어지지만, (−π, π]의 범위를 갖는 y / x의 아크탄젠트를 계산합니다. 다시 말해서, atan2(y, x)는 평면의 양의 x-축과 그것 위에 점 (x, y) 사이의 각도이며, 반시계방향 각도 (위쪽 반-평면, y > 0)에 대해 양의 부호와 시계방향 각도 (아래쪽 반-평면, y < 0)에 대해 음의 기호를 가집니다. 그것은 많은 컴퓨터 프로그래밍 언어에서 처음 도입되었지만, 그것은 역시 이제 과학과 공학의 다른 분야에서 공통적입니다.

표준 아크탄젠트 함수의 관점에서, 그것은 $-\frac{\pi }{2},\frac{\pi }{2})$ (−π/2, π/2)의 범위를 가지면, 그것은 다음처럼 표현될 수 있습니다:

${\displaystyle \mathrm{atan}2(y,x)=\{\begin{array}{ll}\arctan \left(\frac{y}{x}\right)& x>0\\ \arctan \left(\frac{y}{x}\right)+\pi & y\ge 0,x<0\\ \arctan \left(\frac{y}{x}\right)-\pi & y<0,x<0\\ \frac{\pi }{2}& y>0,x=0\\ -\frac{\pi }{2}& y<0,x=0\\ \text{undefined}& y=0,x=0\end{array}}$

그것은 역시 복소수(complex number) x + iy의 편각(argument)의 주요 값(principal value)과 같습니다.

위 함수의 이 제한된 버전은 역시 다음과 같이 탄젠트 절반-각도 공식(tangent half-angle formula)을 사용하여 정의될 수 있습니다:

${\displaystyle \mathrm{atan}2(y,x)=2\arctan \left(\frac{y}{\sqrt{x^2+y^2}+x}\right)}$

x > 0 또는 y ≠ 0 중 하나라는 조건에서 그렇습니다. 어쨌든, 이것은 x ≤ 0 및 y = 0가 주어지면 실패하므로 표현식이 계산 사용에 적합하지 않습니다.

위의 편각 순서 (y, x)가 가장 공통적으로 보이고, 특히 C 프로그래밍 언어와 같은 ISO 표준에서 사용되지만, 일부 저자는 반대 관례 (x, y)을 사용할 수 있으므로 약간의 주의가 필요합니다. 이들 변형은 atan2에 자세히 설명되어 있습니다.

Arctangent function with location parameter

많은 응용에서, 방정식 $x=\tan (y)$의 해 $y$는 주어진 값 $-\mathrm{\infty }<\eta <\mathrm{\infty }$에 최대한 가깝게 하는 것입니다. 적절한 해는 매개변수 수정된 아크탄젠트 함수에 의해 생성됩니다:

${\displaystyle y={\arctan }_{\eta }(x):=\arctan (x)+\pi \mathrm{rni}\left(\frac{\eta -\arctan (x)}{\pi }\right).}$

함수 $\mathrm{rni}$는 가장 가까운 정수로 반올림합니다.

Numerical accuracy

0과 π에 가까운 각도에 대해, 아크코사인은 나쁜-조건된(ill-conditioned) 것이고 따라서 (제한된 자릿수의 숫자로 인해) 컴퓨터 구현에서 감소된 정확도를 갖는 각도를 계산할 것입니다. 유사하게, 아크사인은 −π/2와 π/2에 가까운 각도에 대해 부정확합니다.

See also

• List of integrals of inverse trigonometric functions
• List of trigonometric identities
• Trigonometric function

External links

 

• Weisstein, Eric W. "Inverse Tangent". MathWorld.