수학(mathematics)에서, 정사각 행렬(square matrix)은 행과 열의 개수가 같은 행렬(matrix)입니다. \(n \times n\) 행렬은 \(n\)차 정사각 행렬로 알려져 있습니다. 같은 차수의 두 정사각 행렬은 더하거나 곱할 수 있습니다.
정사각 행렬은 종종 전단(shearing) 또는 회전(rotation)과 같은 단순 선형 변환(linear transformations)을 나타내기 위해 사용됩니다. 예를 들어, 만약 \(R\)이 회전을 나타내는 정사각 행렬 (회전 행렬)이고 \(\mathbf{v}\)가 공간에서 점(position)의 위치를 설명하는 열 벡터(column vector)이면, 곱 \(R\mathbf{v}\)는 해당 회전 후 해당 점의 위치를 설명하는 또 다른 열 벡터를 산출합니다. 만약 \(\mathbf{v}\)가 행 벡터(row vector)이면, 같은 변환은 \(\mathbf{v}R^{\mathsf T}\)를 사용하여 얻을 수 있으며, 여기서 \(R^{\mathsf T}\)는 \(R\)의 전치(transpose)입니다.
Main diagonal
엔트리 \(a_{ii}\) (i = 1, …, n)는 정사각 행렬의 주요 대각선을 형성합니다. 그것들은 행렬의 꼭대기 왼쪽 모서리에서 바닥 오른쪽 모서리까지 이어지는 허수 직선 위에 놓입니다. 예를 들어, 위의 4×4 행렬의 주요 대각선은 원소 \(a_{11}=9, a_{22}=11, a_{33}=4, a_{44}=10\)를 포함합니다.
꼭대기 오른쪽에서 바닥 왼쪽 모서리까지 정사각 행렬의 대각선은 역-대각선(antidiagonal) 또는 반대-대각선(counterdiagonal)이라고 불립니다.
Special kinds
Diagonal or triangular matrix
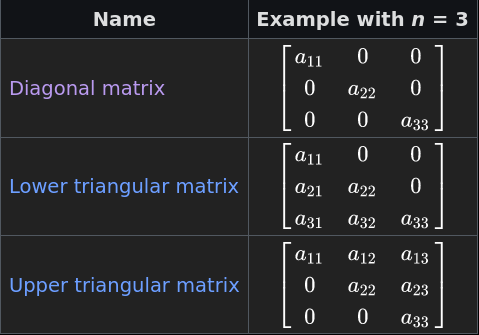
만약 주요 대각선 밖의 모든 엔트리가 영이면, \(A\)는 대각 행렬(diagonal matrix)이라고 불립니다. 만약 주요 대각선 위 (또는 아래)의 모든 엔트리만 영이면, \(A\)는 위쪽 (또는 아래쪽) 삼각 행렬(triangular matrix)이라고 불립니다.
Identity matrix
크기 \(n\)의 항등 행렬(identity matrix) \(I_n\)은 주요 대각선(main diagonal) 위의 모든 원소가 1이고 모든 다른 원소가 0인 \(n \times n\) 행렬입니다. 예를 들어,
\(\quad
I_1 = \begin{bmatrix} 1 \end{bmatrix}
,\
I_2 = \begin{bmatrix}
1 & 0 \\
0 & 1
\end{bmatrix}
,\ \ldots ,\
I_n = \begin{bmatrix}
1 & 0 & \cdots & 0 \\
0 & 1 & \cdots & 0 \\
\vdots & \vdots & \ddots & \vdots \\
0 & 0 & \cdots & 1
\end{bmatrix}.
\)
그것은 차수 \(n\)의 정사각 행렬이고, 특수한 종류의 [[diagonal matrix|대각 행렬(diagonal matrix)]]입니다. 그것은 항등 행렬이라고 불리는데 왜냐하면 그것과의 곱셈은 행렬을 변경하지 않고 남겨두기 때문입니다.
\(\quad AI_n = I_m A = A\mbox{ for any m-by-n matrix }A.\)
Invertible matrix and its inverse
정사각 행렬 \(A\)는 만약 다음임을 만족하는 행렬 \(B\)가 존재하면 역-가능(invertible) 또는 비-특이(non-singular)라고 불립니다:
\(\quad AB = BA = I_n.\)
만약 \(B\)가 존재하면, 그것은 고유하고 \(A\)의 역 행렬(inverse matrix)이라고 불리고, \(A^{-1}\)로 표시됩니다.
Symmetric or skew-symmetric matrix
그것의 전치와 같은 정사각 행렬 \(A\), 즉, \(A^{\mathsf T}=A\)인 행렬은 대칭 행렬(symmetric matrix)이라고 불립니다. 만약 대신 \(A^{\mathsf T}=-A\)이면, \(A\)는 반-대칭 행렬(skew-symmetric matrix)이라고 불립니다.
복소수 정사각 행렬 \(A\)에 대해, 종종 전치의 적절한 아날로그는 \(A\)의 복소 켤레(complex conjugate)의 전치로 정의되는 켤레 전치(conjugate transpose) \(A^*\)입니다. \(A^*=A\)를 만족시키는 복소수 정사각 행렬 \(A\)는 에르미트 행렬(Hermitian matrix)이라고 불립니다. 만약 대신 \(A^*=-A\)이면, \(A\)는 반-에르미트 행렬(skew-Hermitian matrix)이라고 불립니다.
스펙트럼 정리(spectral theorem)에 의해, 실수 대칭 (또는 복소수 에르미트) 행렬은 직교 (또는 유니태리) 고유기저(eigenbasis)를 가집니다; 즉, 모든 각 벡터는 고유벡터의 선형 조합(linear combination)으로 표현할 수 있습니다. 둘 다 경우에서, 모든 고윳값은 실수입니다.
Definite matrix

대칭 \(n \times n\) 행렬은 만약 모든 비-영 벡터 \(x \in \mathbb{R}^n\)에 대해, 다음에 의해 주어진 결합된 이차 형식(quadratic form)이
\(\quad Q(\mathbf{x})=\mathbf{x}^{\text{T}}A\mathbf{x}\)
오직 양수 값 (각각 오직 음수 값; 일부 음수와 일부 양수 둘 다 값)을 취하면 양수-한정 (각각 음수-한정; 부정)이라고 불립니다. 만약 이차 형식이 오직 비-음의 (각각 오직 비-양의 값) 값을 취하면, 대칭 행렬은 양수-반한정 (각각, 음수-반한정)이라고 불립니다; 따라서 그 행렬은 정확히 양수-반한정도 아니고 음수-반한정도 아닐 때 부정입니다.
대칭 행렬이 양수-한정인 것과 모든 그것의 고윳값이 양수인 것은 필요충분 조건입니다. 오른쪽에서 테이블은 2×2 행렬에 대한 두 가능성을 보여줍니다.
두 개의 서로 다른 벡터를 입력으로 허용하면 대신 \(A\)에 결합된 쌍선형 형식(bilinear form)이 생성됩니다:
\(\quad B_A (\mathbf{x}, \mathbf{y}) = \mathbf{x}^{\text{T}}A \mathbf{y}.\)
Orthogonal matrix
직교 행렬(orthogonal matrix)은 열과 행이 직교 단위 벡터(orthogonal unit vectors, 즉, 직교-정규 벡터)인 실수 엔트리를 갖는 정사각 행렬(square matrix)입니다. 동등하게, 행렬 \(A\)는 만약 그것의 전치(transpose)가 그것의 역(inverse)과 같으면 직교입니다:
\(\quad A^\textsf{T}=A^{-1}, \)
이는 다음을 동반합니다:
\(\quad A^\textsf{T} A = A A^\textsf{T} = I, \)
여기서 \(I\)는 항등 행렬(identity matrix)입니다.
직교 행렬 \(A\)는 필연적으로 역가능(invertible) (역 \(A^{-1}=A^\textsf{T} \)), 유니태리(unitary) (\(A^{-1}=A^{\ast} \)), 및 정규(normal) (\(A^{\ast}A=AA^{\ast} \))입니다. 임의의 직교 행렬의 행렬식(determinant)은 +1 또는 −1 중 하나입니다. 특수 직교 그룹(special orthogonal group) \(\operatorname{SO}(n)\)은 행렬식(determinant) +1을 갖는 \(n \times n\) 직교 행렬로 구성됩니다.
직교 행렬의 복소수(complex) 아날로그는 유니태리 행렬(unitary matrix)입니다.
Normal matrix
실수 또는 복소수 정사각 행렬 \(A\)는 만약 \(A^* A = AA^*\)이면 정규(normal)라고 불립니다. 만약 실수 정사각 행렬이 대칭, 반-대칭, 또는 직교이면, 그것은 정규입니다. 만약 복소수 정사각 행렬이 에르미트, 반-에르미트 또는 유니태리이면, 그것은 정규입니다. 정규 행렬은 방금 나열된 행렬 유형을 포함하고 스펙트럼 정리(spectral theorem)가 유지하는 가장 광범위한 행렬 클래스를 형성하기 때문에 주로 관심의 대상입니다.
Operations
Trace
정사각 행렬 \(A\)의 대각합(trace), tr(\(A\))은 대각 엔트리의 합입니다. 행렬 곱셈은 교환적이 아니지만, 두 행렬의 곱의 대각합은 인수의 순서와 무관합니다:
\(\quad \operatorname{tr}(AB) = \operatorname{tr}(BA).\)
이것은 행렬 곱셈의 정의에서 바로 나타납니다:
\(\quad\displaystyle \operatorname{tr}(AB) = \sum_{i=1}^m \sum_{j=1}^n A_{ij} B_{ji} = \operatorname{tr}(BA).\)
역시, 행렬의 대각합은 전치의 대각합과 같습니다. 즉,
\(\quad \operatorname{tr}(A) = \operatorname{tr}(A^{\mathrm T}).\)
Determinant
정사각 행렬 \(A\)의 행렬식 \(\det(A)\) 또는 \(|A|\)는 행렬의 특정 속성을 인코딩하는 숫자입니다. 행렬이 역-가능인 것과 그것의 행렬식이 비-영인 것은 필요충분 조건입니다. 그 절댓값은 단위 정사각형 (또는 정육면체)의 이미지의 넓이 (\(\mathbb{R}^2\)) 또는 부피 (\(\mathbb{R}^3\))와 같고, 그 부호는 해당 선형 맵의 방향에 해당합니다: 행렬식이 양수인 것과 방향이 보존되는 것은 필요충분 조건입니다.
2×2 행렬의 행렬식은 다음에 의해 주어집니다:
\(\quad \det \begin{bmatrix} a&b \\ c&d \end{bmatrix} = ad - bc.\)
3×3 행렬의 행렬식은 6 항 (사뤼스의 규칙(rule of Sarrus))을 포함합니다. 더 긴 라이프니츠 공식(Leibniz formula)은 이들 두 공식을 모든 차원으로 일반화합니다.
정사각 행렬 곱의 행렬식은 행렬식의 곱과 같습니다:
\(\quad \det(AB) = \det(A) \cdot \det(B)\)
임의의 행의 배수를 또 다른 행에 더하거나, 임의의 열의 배수를 또 다른 열에 더해도 행렬식은 변경되지 않습니다. 두 행 또는 두 열을 교환하는 것은 행렬식에 −1을 곱함으로써 행렬식에 영향을 미칩니다. 이들 연산을 사용하여, 임의의 행렬은 아래쪽 (또는 위쪽) 삼각 행렬로 변환할 수 있고, 그러한 행렬에 대해 행렬식은 주요 대각선에 있는 엔트리의 곱과 같습니다; 이것은 임의의 행렬의 행렬식을 계산하는 방법을 제공합니다. 마지막으로, 라플라스 전개(Laplace expansion)는 소행렬식(minors), 즉 더 작은 행렬의 행렬식의 관점에서 행렬식을 표현합니다. 이 전개는 행렬식의 재귀적 정의에 사용될 수 있으며 (시작 사례로 고유한 엔트리인 1×1 행렬의 행렬식, 또는 1인 0×0 행렬의 행렬식을 취함), 라이프니츠 공식과 동등하다고 볼 수 있습니다. 행렬식은 크라메르의 규칙(Cramer's rule)을 사용하여 선형 시스템(linear systems)을 풀기 위해 사용될 수 있으며, 여기서 두 개의 관련된 정사각 행렬의 행렬식의 나눗셈은 각 시스템 변수의 값과 같게 합니다.
Eigenvalues and eigenvectors
다음을 만족시키는 숫자 λ와 비-영 벡터 \(\mathbf{v}\)는
\(\quad A \mathbf{v} = \lambda \mathbf{v}\)
각각, \(A\)의 고윳값(eigenvalue)과 고유벡터(eigenvector)라고 불립니다. 숫자 λ가 n×n-행렬 \(A\)의 고윳값인 것과 \(A-\lambda I_n\)이 역-가능인 것은 필요충분 조건이며, 이는 다음과 동등(equivalent)합니다:
\(\quad \det(A-\lambda I) = 0.\)
행렬식 \(\det (XI_n-A)\)의 평가에 의해 주어진 불확정(indeterminate) X에서 다항식 \(p_A\)는 A의 특성 다항식(characteristic polynomial)이라고 불립니다. 그것은 차수(degree) n의 일계수 다항식(monic polynomial)입니다. 그러므로, 다항 방정식 \(p_A(\lambda)=0\)은 많아야 n개의 서로 다른 해, 즉 행렬의 고윳값을 가집니다. 그것들은 A의 엔트리가 실수이더라도 복소수일 수 있습니다. 케일리-해밀턴 정리(Cayley–Hamilton theorem)에 따르면, \(p_A(A)=0\), 즉, 행렬 자체를 자체의 특성 다항식에 대입한 결과 영 행렬(zero matrix)을 산출합니다.
References
- Brown, William C. (1991), Matrices and vector spaces, New York, NY: Marcel Dekker, ISBN 978-0-8247-8419-5
- Horn, Roger A.; Johnson, Charles R. (1985), Matrix Analysis, Cambridge University Press, ISBN 978-0-521-38632-6
- Mirsky, Leonid (1990), An Introduction to Linear Algebra, Courier Dover Publications, ISBN 978-0-486-66434-7
External links
- Media related to Square matrix at Wikimedia Commons


