수학(mathematics)에서, 부호(sign)의 개념은 모든 각 실수(real number)가 양수, 음수(negative) 또는 영(zero) 중 하나인 속성으로부터 비롯됩니다. 지역 관례에 따라, 영은 양수도 아니고 음수도 아닌 것 (그것 자체의 부호를 가지지 않거나 특정 부호가 없음), 또는 음수와 양수 둘 다에 속하는 것 (두 기호 모두 포함)으로 여겨집니다. 특별히 언급되지 않았을 때, 이 기사는 첫 번째 관례를 준수합니다.
비록 일부 문맥에서, 그것은 (컴퓨터 내에서 실수의 부동-점 표현(floating-point representations)과 같은) 부호화된 영(signed zero)을 고려하는 것이 합리적입니다. 수학 및 물리학에서, 문구 "부호의 변경"은 이 구성을 허용하는 모든 대상의 덧셈의 역(additive inverse) (부정 또는 −1에 의한 곱셈)의 생성과 연관되고, 실수로 제한되지 않습니다. 그것은 양수, 음수 또는 영 중 오직 하나로 규정되지 않은 벡터, 행렬, 및 복소수에 다른 대상 사이에 적용됩니다. 단호 "부호"는 역시 종종 홀수와 짝수 (순열의 부호(sign of a permutation)), 방향(orientation) 또는 회전 (cw/ccw), 한-쪽 극한(one sided limit), 및 아래 § Other meanings에서 묘사된 다른 개념과 같은 양수성과 음수성을 닮은 수학적 대상의 다른 이항 관점을 나타내기 위해 사용됩니다.
Sign of a number
정수(integers), 유리수(rationals), 복소수(complex number), 쿼터니언(quaternion), 옥토니언(octonion), 등과 같은 다양한 숫자 시스템으로부터 숫자(Number)는 숫자의 특정 속성을 마련하는 여러 속성을 가질 수 있습니다. 만약 숫자 시스템이 순서화된 링(ordered ring), 예를 들어, 정수의 구조를 지니면, 그것이 그것에 더해질 때 임의의 숫자를 변경하지 않는 숫자 (덧셈의 항등 원소(identity element))를 포함해야 합니다. 이 숫자는 일반적으로 0으로 표시됩니다. 이 링에서 전체 순서(total order) 때문에, 양의 숫자라고 불리는, 영보다 큰 숫자가 있습니다. 링 내에 요구된 다른 속성에 대해, 각 그러한 양수에 대해 영보다 작은 숫자가 존재하며, 양수에 더해질 때, 결과 0을 산출합니다. 0보다 작은 이들 숫자는 음의 숫자라고 불립니다. 각 그러한 쌍에서 숫자는 각각의 덧셈의 역(additive inverse)입니다. 독점적으로 영 (0), 양수 (+), 또는 음수 (−) 중 하나인, 숫자의 이 속성은 그것의 부호라고 불리고, 종종 각각 실수 0, 1, 및 −1로 인코딩됩니다 (부호 함수(sign function)가 정의되는 방법과 유사합니다). 유리수와 실수는 역시 순서화된 링 (심지어 필드(fields))이므로, 이들 숫자 시스템은 같은 부호 속성을 공유합니다.
산술(arithmetic)에서, 빼기 기호는 보통 뺄셈의 이항 연산을 나타내는 것으로 생각되지만, 대수(algebra)에서, 그것은 보통 피연산자의 덧셈의 역(additive inverse) (때때로 부정이라고 불림)을 산출하는 단항 연산(unary operation)을 나타내는 것으로 생각됩니다. 0은 그 자신의 덧셈의 역 (−0 = 0)이지만, 양수의 덧셈의 역은 음수이고, 음수의 덧셈의 역은 양수입니다. 이 연산의 이중 적용은 −(−3) = 3으로 쓰입니다. 더하기 기호는 대수에서 주로 덧셈의 이항 연산을 표시하기 위해 사용되고, 오직 표현의 양수성을 강조하는 경우는 드뭅니다.
(산술(arithmetic)과 다른 곳에서 사용되는) 공통 숫자-표시 표기법(numeral notation)에서, 숫자의 부호는 종종 숫자 앞에 더하기 또는 빼기 기호(a plus or a minus sign)를 배치함으로써 명시적으로 만들어집니다. 예를 들어, +3은 "양의 삼"를 나타내고, −3은 "음의 삼" (대수적으로 : 3의 덧셈의 역)를 나타냅니다. 특정 문맥없이 (또는 명시적 부호가 주어지지 않았을 때), 숫자는 기본적으로 양수로 해석됩니다. 이 표기법은 음의 기호 "−"와 음수와, 더하기 기호 "+"와 양수와의 강력한 연관성을 설립합니다.
Sign of zero
영(zero)이 양수도 아니고 음수도 아니라는 관례 내에서, 특정 부호-값 0은 숫자 값 0에 할당될 수 있습니다. 이것은 실수에 대해 정의 것처럼 \(\text{sgn}\)-함수에서 악용됩니다. 산술에서, +0과 −0 둘 다는 같은 숫자 0을 나타냅니다. 비록 두 부호 모두를 0에 할당하는 관례가 이 식별에 대해 즉시 허용되지는 않을지라도, 일반적으로 값을 부호와 혼동할 위험은 없습니다.
일부 문맥, 특히 컴퓨팅(computing)에서, 부호화된 영이 다른, 이산 숫자 표현을 참조하는 것과 함께, 부호화된 영(signed zero)의 버전을 고려하는 것이 유용합니다 (자세한 것에 대해 부호화된 숫자 표현(signed number representations)을 참조하십시오).
기호 +0과 −0 은 한-쪽 극한(one-sided limit) (각각, 오른-쪽 극한과 왼-쪽 극한)에 대해 미적분(calculus)과 수학적 해석(mathematical analysis)에서 사용되는 \(0^+\)과 \(0^-\)에 대한 대체로 드물게 나타납니다. 이 표기법은 실수 입력 변수가 양수 (각각, 음수) 값을 따라 0에 접근할 때 함수의 동작을 참조합니다; 두 극한은 존재하거나 같을 필요는 없습니다.
Terminology for signs
0이 양수도 아니고 음수도 아니라고 말할 때, 다음 문구는 숫자의 부호를 참조할 것입니다:
- 숫자는 만약 그것이 영보다 크면 양수입니다.
- 숫자는 만약 그것이 영보다 작으면 음수입니다.
- 숫자는 만약 그것이 영보다 크거나 같으면 비-음수입니다.
- 숫자는 만약 그것이 영보다 작거나 같으면 비-양수입니다.
0이 양수와 음수 둘 다로 말할 때, 수정된 문구가 숫자의 부호를 참조하기 위해 사용됩니다:
- 숫자는 만약 그것이 영보다 크면 엄격하게 양수입니다.
- 숫자는 만약 그것이 영보다 작으면 엄격하게 음수입니다.
- 숫자는 만약 그것이 영보다 크거나 같으면 양수입니다.
- 숫자는 만약 그것이 영보다 작거나 같으면 음수입니다.
예를 들어, 실수의 절댓값(absolute value)은 항상 "비-음수"이지만, 첫 번째 해석에서 반드시 "양수"는 아니지만, 두 번째 해석에서, 그것은 비록 "엄격하게 양수"는 아닐지라도 "양수"라고 불립니다.
같은 용어는 때때로 실수 또는 다른 부호화된 값을 산출하는 함수(functions)에 대해 사용됩니다. 예를 들어, 함수는 만약 그것의 값이 모메인의 모든 인수에 대해 양수이면 양의 함수라고 불리거나, 만약 그것의 값의 모두가 비-음수이면 비-음의 함수라고 불립니다.
Complex numbers
복소수는 순서화가 불가능하므로, 그것들은 순서화된 링의 구조를 수행할 수 없고, 그에 따라서, 양의 및 음의 복소수로 분할될 수 없습니다. 그것들은, 어쨌든, 절댓값(absolute value) 또는 크기(magnitude)라고 불리는 속성을 실수와 공유합니다. 크기는 항상 비-음의 실수이고, 양의 실수, 그것의 절댓값(absolute value)에 속하는 임의의 비-영 숫자가 있습니다.
예를 들어, −3의 절댓값과 3의 절댓값은 3의 절댓값과 둘 다 같습니다. 이것은 기호에서 |−3| = 3 and |3| = 3로 쓰입니다.
일반적으로, 어떤 임의의 실수 값은 그것의 크기와 그것의 부호에 의해 지정될 수 있습니다. 표준 인코딩을 사용하여, 임의의 실수 값은 표준 인코딩에서 크기와 부호의 곱에 의해 주어집니다. 이 관계는 복소수에 대해 부호(sign)를 정의하기 위해 일반화될 수 있습니다.
실수와 복소수 둘 다는 필드를 형성하고 양의 실수를 포함하므로, 그것들은 역시 비-영 숫자의 크기의 역수를 포함합니다. 이것은 임의의 비-영 숫자가 그것의 크기의 역수와 곱해지게, 즉, 그것의 크기로 나뉠 수 있습니다. 크기에 의한 비-영 실수의 몫은 정확히 그것의 부호를 산출하는 것은 즉각적입니다. 아날로그에 의해, 복소수 z의 부호는 z의 몫과 |z|의 크기로 정의될 수 있습니다. 복소수의 크기는 분리되기 때문에, 복소수의 결과 부호는 어떤 의미에서 그것의 복소 편각을 나타냅니다. 이것은 \(\displaystyle e^{i\pi}= -1\)를 제외하고 실수의 부호와 비교되는 것입니다. 복소 부호-함수의 정의에 대해, 아래 § Complex sign function를 참조하십시오.
Sign functions

숫자를 다룰 때, 종종 부호를 숫자로 사용하는 것이 편리합니다. 이것은 임의의 숫자의 부호를 추출하고, 그것을 추가 계산에 사용할 수 있도록 하기 전에 미리-정의된 값에 그것을 매핑하는 함수에 의해 수행됩니다. 예를 들어, 오직 양수 값에 대해 복잡한 알고리듬을 공식화하고, 나중에 오직 부호를 처리하는 것이 유리할 수 있습니다.
Real sign function
부호 함수(sign function 또는 signum function)는 실수의 집합을 세 실수의 집합 \(\displaystyle \{-1,\; 0,\; 1\}\)으로 매핑함으로써 실수의 부호를 추출합니다. 그것은 다음처럼 정의될 수 있습니다:
\(\quad\displaystyle \text{sgn}: \mathbb R \to \{x\in \mathbb R : |x|= 1\}\cup \{0\}\)
\(\quad\displaystyle x \mapsto \text{sgn}(x) = \begin{cases}
-1 & \text{if } x < 0, \\
~~\, 0 & \text{if } x = 0, \\
~~\, 1 & \text{if } x > 0. \end{cases}\)
따라서, sgn(x)는 x가 양수일 때 1이고, sgn(x)는 x가 음수일 때 −1입니다. x의 비-영 값에 대해, 이 함수는 역시 다음 공식에 의해 정의될 수 있습니다:
\(\quad\displaystyle \text{sgn}(x) = \frac{x}{|x|} = \frac{|x|}{x}\),
여기서 |x|는 x의 절댓값(absolute value)입니다.
Complex sign function
실수는 1-차원 방향을 가지지만, 복소수는 2-차원 방향을 가집니다. 복소수 부호 함수는 그것의 인수 z = x + iy의 크기(magnitude)를 욕구하며, 다음과 같이 계산될 수 있습니다:
\(\quad\displaystyle |z| = \sqrt{z\bar z} = \sqrt{x^2 + y^2}.\)
위에 것과 유사하게, 복소수 부호 함수는 비-영 복소수를 단일-모듈러 복소수의 집합과 0을 0: \(\displaystyle \{z\in \mathbb C : |z|= 1\}\cup \{0\}\)으로 매핑함으로써 복소수의 복소수 부호를 추출합니다. 그것은 다음처럼 정의될 수 있습니다:
z를 역시 그것의 크기와 편각 φ 중 하나에 의해 표현된 \(z=|z| e^{\i\varphi}\)로 놓습니다. 그런-다음
\(\quad\displaystyle \text{sgn}(z) = \begin{cases} 0 &&\text{for } z=0\\
\displaystyle\frac{z}{|z|} = e^{i\varphi} &&\text{otherwise}.\end{cases}\)
이 정의는 역시 정규화된 벡터, 즉, 그것의 방향이 변하지 않고, 그것의 길이가 단위(unity)로 고정된 벡터로 인식될 수 있습니다. 만약 원래 값이 극 형식에서 R,θ이면, sign(R, θ)는 1 θ입니다. sign() 또는 signum()을 차원의 임의의 숫자로의 확장은 분명하지만, 이것은 이미 벡터를 정규화하는 것으로 정의되어 왔습니다.
Signs per convention
속성에 대해 같은 기초 위에 정확히 두 가지 가능성이 있는 상황에서, 이것들은 종종, 각각, 관례에 의해 더하기 및 빼기로 레이블됩니다. 어떤 상황에서, 이 할당 (즉, 그것의 값의 범위가 양수로 고려되는 것과 음수로 고려되는 것)의 선택이 자연스럽지만, 다른 문맥에서, 그 선택이 임의적이며, 필요한 명시적인 부호 규칙을 만들며, 유일한 요구 사항은 관례의 일관된 사용입니다.
Sign of an angle

많은 상황에서, 부호를 각도, 특히 방향화된 각도 또는 회전(rotation)의 각도의 측정과 연관시키는 것이 공통적입니다. 그러한 상황에서, 부호는 각도가 시계-방향(clockwise)인지 반-시계-방향인지 여부를 가리킵니다. 비록 다른 관례가 사용될 수 있을지라도, 수학(mathematics)에서 반-시계-방향 각도는 양수로 세고, 시계-방향 각도는 음수로 세는 것이 공통적입니다.
역시 회전의 축(axis of rotation)이 방향화되었다고 가정하여, 부호를 삼 차원에서 회전의 각도에 결합하는 것이 가능합니다. 특히, 방향화된 축을 중심으로 오른손(right-handed) 회전은 전형적으로 양수로 세지만, 왼손 회전은 음수로 셉니다.
Sign of a change
양 x가 시간에 걸쳐 변할 때, x의 값에서 변화(change)는 전형적으로 다음 방정식에 의해 정의됩니다:
\(\quad\displaystyle \Delta x = x_\text{final} - x_\text{initial}. \)
이 관례를 사용하여, x에서 증가는 양의 변화를 세지만, x의 감소는 음의 변화를 셉니다. 미적분(calculus)에서, 이 같은 관례는 도함수(derivative)의 정의에서 사용됩니다. 결과로써, 임의의 증가하는 함수(increasing function)는 양의 도함수를 가지지만, 임의의 감소하는 함수는 음의 도함수를 가집니다.
Sign of a direction
해석적 기하학(analytic geometry)과 물리학(physics)에서, 특정 방향을 양수 또는 음수로 이름-짓는 것이 공통적입니다. 기본 예제에 대해, 숫자 직선(number line)은 보통 오른쪽으로 양수를 그리고, 왼쪽으로 음수를 그립니다:

결과로, 선형 운동(linear motion), 변위(displacement) 또는 속도(velocity)를 논의할 때, 오른쪽으로 운동은 보통 양수인 것으로 생각되지만, 왼쪽으로 유사한 운동은 음수인 것으로 생각됩니다.
데카르트 평면(Cartesian plane) 위에서, 오른쪽과 위쪽 방향은 보통 양수인 것으로 생각되며, 오른쪽은 양의 x-방향이고, 위쪽은 양의 y-방향입니다. 만약 변위 또는 속도 벡터(vector)가 벡터 성분(vector component)으로 분리되면, 수평 부분은 오른쪽 운동에 대해 양수일 것이고 왼쪽으로 운동에 대해 음수일 것이지만, 수직 부분은 위쪽 운동에 대해 양수일 것이고 아래쪽 운동에 대해 음수일 것입니다.
Signedness in computing
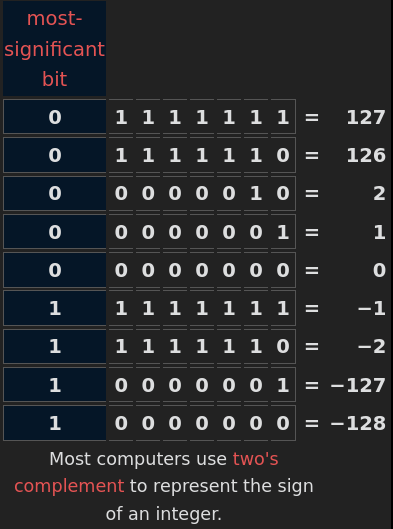
컴퓨팅(computing)에서, 정수 값은 부호화된 것 또는 비-부호화된 것 중 하나일 수 있으며, 컴퓨터가 숫자에 대한 부호를 추적하는지 여부에 따라 다릅니다. 정수 변수(variable)를 오직 비-음의 값으로 제한함으로써, 하나보다 많은 비트(bit)가 숫자의 값을 저장하는 것에 대해 사용될 수 있습니다. 컴퓨터 내에서 정수 산술이 수행되는 방법 때문에, 부호화된 숫자 표현(signed number representation)은 보통 부호를 단일 독립 비트로 저장하지 않고, 대신 예를 들어 이의 보수(two's complement)를 사용합니다.
반대로, 실수는 부동 점(floating point) 값으로 저장되고 조작됩니다. 부동 점 값은 세 가지 분리된 값, 가수, 지수, 및 부호를 사용하여 표시됩니다. 이 분리된 부호 비트가 주어지면, 양의 및 음의 영 둘 다를 나타내는 것이 가능합니다. 대부분의 프로그래밍 언어는 전형적으로 양의 영과 음의 영을 동등한 값으로 처리하지만, 그것들은 구별이 감지될 수 있는 수단을 제공합니다.
Other meanings
실수의 부호 외에도, 단어 부호는 역시 수학과 다른 과학 전반에 걸쳐 다양한 관련된 방법에서 사용됩니다:
- 단어 부호까지는, 양 q에 대해, 특정 Q에 대해 q = Q 또는 q = −Q 중 하나가 알려져 있음을 의미합니다. 그것은 종종 q = ±Q으로 표현됩니다. 실수에 대해, 그것은 오직 양의 절댓값(absolute value) |q|이 알려져 있음을 의미합니다. 복소수(complex numbers)와 벡터(vectors)에 대해, 부호까지 알려진 양은 알려진 크기(magnitude)를 갖는 양보다 더 강한 조건입니다: Q와 −Q를 별도로 하고, |q| = |Q|를 만족하는 q의 많은 다른 가능한 값이 있습니다.
- 순열의 부호(sign of a permutation)는 만약 순열이 짝수이면 양수인 것이고 순열이 홀수이면 음수인 것으로 정의됩니다.
- 그래프 이론(graph theory)에서, 부호화된 그래프(signed graph)는 각 가장자리가 양 또는 음의 부호로 표시된 그래프입니다.
- 수학적 해석학(mathematical analysis)에서, 부호화된 측정(signed measure)은 집합의 측정(measure)이 양 또는 음의 값을 가질 수 있는 측정의 개념의 일반화입니다.
- 부호화된-자릿수 표현(signed-digit representation)에서, 숫자의 각 자릿수는 양 또는 음의 부호를 가질 수 있습니다.
- 부호화된 넓이(signed area)와 부호화된 부피(signed volume)의 아이디어는 때때로 어떤 넓이 또는 부피에 대해 음수로 세는 것이 편리할 때 사용됩니다. 이것은 특히 행렬식(determinant)의 이론에서 참입니다. (추상적인) 방향화된 벡터 공간(oriented vector space)에서, 벡터 공간에 대해 각 순서화된 기저는 양적으로 또는 음적으로 방향화된 것으로 분류될 수 있습니다.
- 물리학(physics)에서, 임의의 전하(electric charge)는 부호, 양수 또는 음수 중 하나로 제공됩니다. 관례에 의해, 양전하는 양성자(proton)와 같은 부호를 가진 전하이고, 음전하는 전자(electron)와 같은 부호를 가진 전하입니다.
References
- "Comprehensive List of Algebra Symbols". Math Vault. 2020-03-25. Retrieved 2020-08-26.
- Weisstein, Eric W. "Sign". mathworld.wolfram.com. Retrieved 2020-08-26.
- "List of Calculus and Analysis Symbols". Math Vault. 2020-05-11. Retrieved 2020-08-26.
- "SignumFunction". www.cs.cas.cz. Retrieved 2020-08-26.
- "Sign of Angles | What is An Angle? | Positive Angle | Negative Angle". Math Only Math. Retrieved 2020-08-26.
