암기 계산(Mental calculation)은 오직 사람의 두뇌(human brain)를 사용하는 산술(arithmetic)적 계산(calculation)으로 구성되며, (연필과 종이 같은) 어떤 용품 또는 계산기(calculator)와 같은 장치의 도움없이 이루어집니다. 사람들은 컴퓨팅 도구가 유용하지 않을 때, 그것이 (전통적인 교육 기관 방법과 같은) 다른 계산의 수단보다 빠를 때, 또는 심지어 경쟁 상황(a competitive context)에서 암기 계산을 사용합니다. 암기 계산은 종종 특정 유형의 문제에 대해 고안된 특정 기법의 사용을 포함합니다. 비정상적으로 높은 암기 계산을 수행하기 위한 능력을 가진 사람들은 암기 계산기(mental calculator) 또는 번개 계산기라고 불립니다.
이러한 기술의 대부분은 십진(decimal) 숫자-표시 시스템의 이점을 취하거나 그것에 의존합니다. 보통, 기수의 선택은 사용할 방법 또는 방법들을 결정하는 것입니다.
Methods and techniques
Casting out nines
두 피연산자(operand)에 산술 연산을 적용하고 결과를 얻은 후, 다음 절차는 결과의 정확성에서 신뢰도를 높이기 위해 사용될 수 있습니다:
- 첫 번째 피연산자의 자릿수를 더합니다; 임의의 9 (또는 9에 더해지는 자릿수의 집합)는 0으로 세어질 수 있습니다.
- 만약 결과 합이 둘 이상의 자릿수를 가지면, 단계 일에서 처럼 그들 자릿수를 더합니다; 결과 합이 오직 한 자리 자릿수가 될 때까지 이 단계를 반복합니다.
- 두 번째 피연산자로 단계 일과 이를 반복합니다. 두 단일-자릿수가 있는데, 하나는 첫 번째 피연산자에서 압축된 것이고 다른 하나는 두 번째 피연산자에서 압축된 것입니다. (이들 단일-자릿수는 역시 우리가 원래 피연산자를 9로 나누면 끝에 남게 되는 나머지 숫자입니다; 수학적으로 말하면, 그것들은 모듈로(modulo) 9의 원래 피연산자입니다.)
- 원래 지정된 연산을 두 압축된 피연산자에 적용하고, 그런-다음 연산 결과에 자릿수-의-합 절차를 적용합니다.
- 원래 계산에 대해 원래 얻어져야 할 결과의 자릿수를 더합니다.
- 만약 단계 4의 결과가 단계 5의 결과와 같지 않으면, 원래 답은 틀린 것입니다. 만약 두 결과가 맞으면, 원래 답은 맞을 수 있지만, 그것이 보장되지는 않습니다.
예제
- 계산 결과 6338 × 79가 500702와 같다고 가정합니다.
- 6338의 자릿수를 더합니다: (6 + 3 = 9이므로, 0으로 셉니다) + 3 + 8 = 11
- 요구에 따라 반복: 1 + 1 = 2
- 79의 자릿수를 더합니다: 7 + (9는 0으로 셉니다) = 7
- 압축된 피연산자에 대해 원래 연산을 수행하고, 자릿수를 더합니다: 2 × 7 = 14; 1 + 4 = 5
- 500702의 자릿수를 더합니다: 5 + 0 + 0 + (7 + 0 + 2 = 9, 이것은 0으로 셉니다) = 5
- 5 = 5이므로, 6338 × 79가 500702와 같다는 예측이 옳을 가능성이 있습니다.
같은 절차는 여러 연산과 함께 사용될 수 있으며, 각 연산에 대해 단계 1과 2를 반복합니다.
Estimation
암기 계산을 확인하는 동안, 스케일링의 관점에서 그것을 생각하는 것이 유용합니다. 예를 들어, 큰 숫자, 말하자면 1531 × 19625를 처리할 때, 추정은 최종 값에 대해 예상되는 자릿수의 숫자를 인식하도록 지시합니다. 확인하는 유용한 방법은 추정하는 것입니다. 1531은 약 1500이고, 19625는 약 20000이므로, 약 20000 × 1500 (30000000)의 결과는 실제 답 (30045875)에 대해 좋은 추정일 것입니다. 따라서 만약 답이 너무 많은 자릿수를 가지면, 실수가 발생한 것입니다.
Factors
곱할 때, 기억해야 할 유용한 점은 피연산자의 인수가 여전히 남는다는 것입니다. 예를 들어, 14 × 15가 211이라고 말하는 것은 비합리적입니다. 15는 5의 배수이므로, 곱도 마찬가지여야 합니다. 마찬가지로, 14는 2의 배수이므로, 곱은 짝수해야 합니다. 게다가, 5와 2 둘 다의 배수인 임의의 숫자는 반드시 10의 배수이고, 십진 시스템에서 0으로 끝납니다. 정답은 210입니다. 그것은 10, 7 (14의 다른 소수 인수) 및 3 (15의 다른 소수 인수)의 배수입니다.
Calculating differences: a − b
Direct calculation
b의 자릿수가 a의 해당 자릿수보다 모두 작을 때, 계산은 자릿수마다 수행될 수 있습니다. 예를 들어, 872 − 41은 단순히 단위 자리에서 2에서 1을 빼고 십 자리에서 7에서 4를 뺌으로써 평가합니다: 831.
Indirect calculation
위의 상황이 적용되지 않을 때, 간접 계산이라고 알려진 또 다른 방법이 있습니다.
Look-ahead borrow method
이 방법은 왼쪽에서 오른쪽으로 숫자를 빼기 위해 사용될 수 있고, 만약 요구되는 모두가 결과를 큰 소리로 읽는 것이면, 임의 크기의 숫자를 빼는데도 사용자의 메모리가 거의 필요하지 않습니다.
한 번에 하나씩 왼쪽에서 오른쪽으로 처리됩니다.
예제:
4075
− 1844
------
천 단위: 4 − 1 = 3, 오른쪽을 보면, 075 < 844이므로, 내림수가 필요합니다.
3 − 1 = 2, "이 천"이라고 말합니다.
우리는 4 − 1이 아닌 3 − 1을 수행하는데 왜냐하면 오른쪽에 열이
천 자리에서 빌릴 것이기 때문입니다.
백 단위: 0 − 8 = 음수는 여기서 허용되지 않습니다.
우리는 왼쪽 열에서 빌려온 숫자 1을 사용함으로써
이 자릿수를 증가할 것입니다. 그러므로:
10 − 8 = 2. 그것은 0이 아닌 10인데, 왜냐하면 천 자리에서 빌려온 일이기 때문입니다.
75 > 44이므로 빌리는 것이 필요하지 않으며,
"이 백"이라고 말합니다
십 단위: 7 − 4 = 3, 5 > 4이므로, 5 - 4 = 1
따라서, 결과는 2231입니다.
Calculating products: a × b
이러한 방법의 대부분은 분배 속성(distributive property) 때문에 작동합니다.
Multiplying any two numbers by attaching, subtracting, and routing
아르티옴 치프라소프(Artem Cheprasov)에 의해 발견된, 사용자에게 셋의 고유한 방법을 통해 임의의 크기의 숫자를 서로 빠르게 곱하기 위한 3 단계를 활용하는 것을 허용하는 곱셈의 방법이 있습니다.
첫째, 그 방법은, 곱셈 속도를 높이기 위해 중간 단계 동안, 숫자를 더하거나 빼는 것과 반대로, 숫자를 서로 붙이는 것을 이용합니다. 예를 들어, 357과 84와 같은 중간 결과를 더하거나 빼는 대신에, 사용자는 곱셈 문제를 단순화하고 신속하게 처리하기 위해 숫자를 함께 덧붙일 수 있습니다 (35784). 숫자를 서로 붙이는 것은 전통적인 곱셈 기법에서 볼 수 있는 불필요한 단계를 우회하는 데 도움이 됩니다.
둘째, 이 방법은 빼기를 통해 곱셈 속도를 높이기 위해, 심지어 두 개의 양의 정수를 곱할 때에도, 필요에 따라 음수를 사용합니다. 이것은 두 개의 양의 정수가 음의 중간 단계를 얻기 위해 곱해질 수 있지만, 결국에는 여전히 올바른 양의 답을 얻을 수 있음을 의미합니다. 이들 음수는 실제로 곱셈 단계 자체에서 자동적으로 유도되고 따라서 특정 문제에 고유합니다. 다시 말하지만, 그러한 음의 중간 단계는 암산 수학을 서두르는 데 도움이 되도록 설계되었습니다.
마지막으로, 이 방법을 사용하는 또 다른 독특한 측면은 사용자가 특정 정수와 함께 주관적 선호도 또는 강점과 약점을 기반으로 당면한 특정 곱셈 문제에 대한 여러 다른 "곱셈의 경로" 중 하나를 선택할 수 있다는 것입니다.
같은 시작하는 정수에도 불구하고, 다른 곱셈 경로는 사용자에 의해 그것들이 곱할 때 자동적으로 유도되는 다른 중간 숫자를 제공합니다. 이들 중개물 중 일부는 다른 것보다 쉬울 수 있습니다 (예를 들어, 일부 사용자는 음수 7을 사용하는 경로를 찾을 수 있지만, 또 다른 경로는 전형적으로 대부분의 사람들에게 암기로 더 쉽게 연산할 수 있지만, 모든 경우에서는 그렇지 않은, 5 또는 0을 사용하는 경로를 찾을 수 있습니다).
만약 한 학생에 대해 다른 경로와 중간 숫자에 비해 하나의 "경로"가 더 어려워 보인다면, 해당 학생은, 심지어 원래 문제가 같은 것일지라도, 단순히 자체에 대해 또 다른 간단한 곱셈의 경로를 선택할 수 있습니다.
The "Ends of Five" Formula
임의의 2 자릿수 x 2 자릿수 곱셈 문제에 대해, 만약 숫자 둘 다가 5로 끝나면, 다음 알고리듬은 그것들을 함께 빠르게 곱하기 위해 사용될 수 있습니다:
\(\quad\displaystyle Ex: 35 \times 75\)
예비 단계는 십의 가장 가까운 배수로 더 작은 숫자를 내림하고 더 큰 숫자를 올립니다. 이 경우에서:
\(\quad\displaystyle 35 - 5 = 30 = X\)
\(\quad\displaystyle 75 + 5 = 80 = Y\)
알고리듬은 다음처럼 읽습니다:
\(\quad\displaystyle (X \times Y) + 50(t_1-t_2) + 25\)
여기서 \(t_1\)은 원래 더 큰 숫자 (75)의 십 단위이고 \(t_2\)는 원대 더 작은 숫자 (35)의 십 단위입니다.
\(\quad\displaystyle = 30 \times 80 + 50(7-3)+25 = 2625\)
저자는 역시 만약 대신에 원래 더 큰 숫자를 내림하고 원래 더 작은 숫자를 올림하기를 원하면 또 다른 유사한 알고리듬을 설명합니다.
The "Borrower's" Formula
만약 두 숫자가 가장 가까운 100의 배수에서 등거리에 있으면, 간단한 알고리듬이 곱을 찾기 위해 사용될 수 있습니다.
간단한 예제로서:
\(\quad\displaystyle 33 \times 67\)
두 숫자는 그들의 가장 가까운 100의 배수 (각각, 0과 100)에서 등거리 (33만큼 멀리)입니다.
예비 단계는 가장 가까운 십의 배수로 더 작은 숫자를 내림하고 더 큰 숫자를 올립니다. 이 경우에서:
\(\quad\displaystyle 33 - 3 = 30 = X\)
\(\quad\displaystyle 67 + 3 = 70 = Y\)
알고리듬은 다음처럼 읽습니다:
\(\quad\displaystyle (X \times Y) + u_1 \times u_2 + u_2(T_1-T_2)\)
여기서 \(u_1\)는 원래 더 큰 숫자 (67)의 단위 자릿수이고 \(u_2\)는 원래 더 작은 숫자 (33)의 단위 자릿수입니다. \(T_1\)은 그들의 각 거듭제곱에 의해 (이 경우에서 십 자릿수에 대해, 10에 의해) 곱해진 원래 더 큰 숫자의 십 자릿수이고 \(T_2\)는 원래 더 큰 숫자의 십 자릿수입니다.
그리고 따라서:
\(\quad\displaystyle (30 \times 70) + 7 \times 3+3(60-30) = 2100+21+90=2211\)
Multiplying any 2-digit numbers
임의의 2-자릿수 숫자를 쉽게 곱하기 위한 간단한 알고리듬은 다음과 같습니다 (여기서 a는 첫 번째 숫자의 십 자리, b는 첫 번째 숫자의 일 자리, c는 두 번째 숫자의 십 자리이고 d는 두 번째 숫자의 일 자리입니다):
\(\quad\displaystyle (10a+b) \cdot (10c+d)\)
\(\quad\displaystyle = 100 (a\cdot c) + 10 (b\cdot c) + 10 (a\cdot d)+ b\cdot d\)
예를 들어,
\(\quad\displaystyle 23\cdot 47 = 100 (2\cdot 4) + 10 (3\cdot 4) + 10 (2\cdot 7)+ 3\cdot 7\)
800
+120
+140
+ 21
-----
1081
이것은 부분 곱의 전통적인 합과 같은 것이며, 단지 간결하게 다시 설명한 것임을 주목하십시오. 일의 메모리에서 유지되는 원소의 숫자를 최소화하기 위해, 먼저 "교차" 곱셈 곱의 합을 수행하고, 그런-다음 다른 두 원소를 더하는 것이 편리할 수 있습니다:
\(\quad\displaystyle (a\cdot d+b\cdot c)\cdot 10 \)
\(\quad\displaystyle {} + b\cdot d\) [그것의 오직 십 자릿수가 첫 번째 항에 간섭할 것입니다]
\(\quad\displaystyle {} + a\cdot c\cdot 100\)
즉, 이 예제에서
(12 + 14) = 26, 26 × 10 = 260,
그것에 21을 더해서: 281이고 그런-다음 800을 더해서: 1081은 쉽게 됩니다.
이것에 대해 기억하기 쉬운 기억법은 FOIL일 것입니다. F는 첫 번째, O는 바깥쪽, I는 안쪽, L은 마지막을 의미합니다. 예를 들어:
\(\quad\displaystyle 75\cdot 23\)
및
\(\quad\displaystyle ab\cdot cd\)
여기서 7은 a, 5는 b, 2는 c 및 3은 d입니다.
다음을 생각해 보십시오:
\(\quad\displaystyle a\cdot c\cdot 100 + (a\cdot d+b\cdot c)\cdot 10 + b\cdot d\)
이 표현은 백, 십, 일 자리를 가진 밑수 10에서 임의의 숫자와 유사합니다. FOIL은 역시 F가 수백, OI가 수십, L이 일을 갖는 숫자로 보일 수 있습니다.
\(\quad\displaystyle a\cdot c\)는 두 수자의 각각의 첫 번째 자릿수의 곱입니다; F.
\(\quad\displaystyle (a\cdot d+b\cdot c)\)는 바깥 자릿수와 안쪽 자릿수의 곱의 합니다; OI.
\(\quad\displaystyle b\cdot d\)는 두 숫자의 각각의 마지막 자릿수의 곱입니다; L.
Multiplying by 2 or other small numbers
곱해지는 하나의 숫자가 임의의 단일 자릿수로 쉽게 곱해질 수 있을 만큼 충분히 작을 때, 곱은 오른쪽에서 왼쪽으로 자릿수마다 쉽게 계산될 수 있습니다. 이것은 2에 의한 곱셈에 대해 특별히 쉬운데 왜냐하면 올림 자숫자가 1을 초과할 수 없기 때문입니다.
예를 들어, 2 × 167을 계산하기 위해: 2×7=14이므로, 첫 번째 자릿수는 4이고, 만들어진 올림수 1과 2×6 = 12와 더해져서 13을 제공하므로, 다음 자릿수는 3이고, 만들어진 올림수 1과 2×1=2과 더해져서 3을 제공합니다. 따라서 곱은 334입니다.
Multiplying by 5
숫자를 5에 곱하기 위해,
1. 먼저 해당 숫자에 10을 곱하고, 그런-다음 그것을 2로 나눕니다. 두 단계는 서로 바꿔 사용할 수 있습니다. 즉, 우리는 숫자를 반으로 줄이고 그런-다음 그것을 곱할 수 있습니다.
다음 알고리듬은 이 결과를 생성하기 위한 빠른 방법입니다:
2. 원했던 숫자의 오른쪽 편에 영을 더합니다. (A.)
3. 다음으로, 가장-왼쪽 수자로부터 시작하여, 2로 나누고 (B.), 각 결과를 새로운 숫자를 형성하기 위해 각각에 덧붙입니다;(분수 답은 가장 가까운 정수로 내림되어야 합니다).
예제: 176에 5를 곱하시오.
A. 176에 영을 더하여 1760을 만듭니다.
B. 왼쪽에서 시작하여 2로 나눕니다.
1. 1을 2로 나누어 .5를 얻고, 영으로 반내림합니다.
2. 7을 2로 나누어 3.5를 얻고, 3으로 반내립합니다.
3. 6을 2로 나누어 3을 얻습니다. 영을 2로 나눈 것은 단순히 영입니다.
결과 숫자는 0330입니다. (이것은 최종 답이 아니지만, 다음 단계에서 조정될 첫 번째 근사입니다:)
C. 2로 나누기 전에 숫자가 홀수였으면, 이 새로운 숫자에서
해당 단일 자릿수 다음에 오는 숫자에 5를 더합니다
예제: 176 (첫 번째, 두 번째 세 번째 자리에서):
1. 첫 번째 자리는 1이며, 이것은 홀수입니다. 새로운 숫자 (0330)에서
첫 번째 자리 다음 자릿수는 3이고, 이것에 5를 더합니다; 3+5=8.
2. 176의 두 번째 자리에서 숫자는 7이고 역시 홀수입니다.
해당하는 숫자 (0 8 3 0)는 마찬가지로 5만큼 증가됩니다;
3+5=8.
3. 176의 세 번째 자리에서 숫자는 6이고, 이것은 짝수입니다.
그러므로, 답에서 마지막 숫자는 0으로 변경되지 않습니다.
마지막 답은 0880입니다.
가장-왼쪽 영은 생략될 수 있으며, 880을 남깁니다.
따라서, 176 곱하기 5는 880과 같습니다.
예제: 288에 5를 곱하시오.
A. 288을 2로 나눕니다. 우리는 각 자릿수를 개별적으로 나눌 수 있고 144를 얻습니다. (더 작은 숫자로 나누는 것은 더 쉽습니다.)
B. 10을 곱합니다. 영을 더하여 결과 1440을 산출합니다.
Multiplying by 9
9 = 10 − 1이므로, 숫자를 9에 곱하기 위해, 그것에 10에 곱하고 그런-다음 결과로부터 원래 숫자를 뺍니다. 예를 들어, 9 × 27 = 270 − 27 = 243.
이 방법은 빼는 숫자를 두 배함으로써 구 대신에 팔에 곱하기 위해 조정될 수 있습니다; 8 × 27 = 270 − (2×27) = 270 − 54 = 216.
비슷하게, 빼는 대신에 더함으로써, 같은 방법은 각각 11과 12를 곱하기 위해 사용될 수 있습니다 (그렇지만 11에 곱하기 위한 더 단순한 방법이 존재합니다).
Using hands: 1–10 multiplied by 9
이 방법을 사용하기 위해, 우리는 손바닥이 그것들을 향하도록 손을 앞에 놓아야 합니다. 왼쪽 엄지 손가락을 1로 할당하고, 왼쪽 두 번째 손가락을 2로 지정하고, 이런 식으로 모든 손가락을 지정하며 오른쪽 엄지 손가락이 십으로 할당됩니다. 각 "|"는 펴진 손가락을 상징하고 "−"는 구부러진 손가락을 나타냅니다.
1 2 3 4 5 6 7 8 9 10
| | | | | | | | | |
왼쪽 손가락 오른쪽 손가락
9에 의해 곱해질 숫자를 나타내는 손가락을 구부립니다.
Ex: 6 × 9는 다음일 것입니다:
| | | | | − | | | |
오른쪽 새끼 손가락이 구부러졌습니다. 구부러진 손가락의 왼쪽에 있는 여전히 펴진 손가락의 개수를 취하고 오른쪽의 손가락 개수 앞에 덧붙입니다.
예를 들어: 오른쪽 새끼 손가락의 왼쪽에 다섯 손가락이 있고 오른쪽 새끼 손락의 오른쪽에 네 손가락이 있습니다. 따라서 6 × 9 = 54.
5 4
| | | | | − | | | |
Multiplying by 10 (and powers of ten)
정수를 10에 곱하기 위해, 간단히 숫자의 끝에 여분의 0을 더하십시오. 비-정수를 10에 곱하기 위해, 십진 점을 오른쪽 한 자리만큼 이동하십시오.
일반적으로 밑수 십에 대해, \(10^n\) (여기서 n은 정수)을 곱하기 위해, 십진 점을 오른쪽으로 n 자리 이동하십시오. 만약 n이 음수이면, 십진 점을 왼쪽으로 |n| 자리 이동하십시오.
Multiplying by 11
단일 자리 숫자에 대해 간단히 숫자를 십 자리까지 복제하십시오, 예를 들어: 1 × 11 = 11, 2 × 11 = 22, ... 9 × 11 = 99.
임의의 더 큰 정수(integer)에 대한 곱은 한 번에 두 개씩 오른쪽에서 왼쪽으로 각 숫자에 일련의 덧셈에 의해 찾아질 수 있습니다.
먼저 일 자리를 가져와서 임시 결과에 그것을 복사하십시오. 다음으로, 승수의 일 자리부터 시작하여, 각 자리를 왼쪽 자리에 더합니다. 각 합은 그런-다음 모든 다른 것들 앞에 결과의 왼쪽에 더해집니다. 만약 숫자의 합이 10 이상이면, 항상 1이 되는 십 자리를 취하고, 그것을 다음 덧셈에 올림하십시오. 마지막으로 가장-왼쪽 (가장 높은 값) 자리 승수를 결과의 앞에 복사하고, 필요하다면 올려진 1을 더하여 최종 곱을 얻습니다.
음수 11, 승수 또는 둘 다의 경우에서, 두 숫자의 보통 곱셈에 따라 최종 곱에 부호를 적용합니다.
759 × 11의 단계별 예제:
- 승수의 일 자리, 9는 임시 결과에 복사됩니다.
- 결과: 9
- 5 + 9 = 14이므로 4는 결과의 왼쪽 편에 위치되고 1을 올립니다.
- 결과: 49
- 비슷하게 7 + 5 = 12를 더하고, 그런-다음 올려진 1을 더해서 13을 얻습니다. 결과의 왼쪽 편에 3을 위치하고 1을 올립니다.
- 결과: 349
- 올려진 1을 승수에서 가장-높은 값 자리에 더하여, 7 + 1 = 8이고, 최종 결과에 복사하십시오.
- 759 × 11의 마지막 곱: 8349
추가적인 예제:
- −54 × −11 = 5 5+4(9) 4 = 594
- 999 × 11 = 9+1(10) 9+9+1(9) 9+9(8) 9 = 10989
- 9+1을 가장-높은 값 자리로 처리함에 주목하십시오.
- −3478 × 11 = 3 3+4+1(8) 4+7+1(2) 7+8(5) 8 = −38258
- 62473 × 11 = 6 6+2(8) 2+4+1(7) 4+7+1(2) 7+3(0) 3 = 687203
또 다른 방법은 단순히 숫자에 10을 곱하고, 결과에 원래 숫자를 더하는 것입니다.
예를 들어:
17 × 11
17 × 10 = 170
170 + 17 = 187
17 × 11 = 187
마지막 쉬운 방법:
만약 우리가 두-자리 숫자를 가지면, 그것을 가져와서 두 숫자를 함께 더하고 해당 합을 원래 두-자리 숫자의 가운데에 넣으면 답을 얻을 수 있습니다.
예를 들어: 24 x 11 = 264인데 왜냐하면 2 + 4 = 6이고 6을 2와 4의 사이에 위치되기 때문입니다.
두 번째 예제: 87 x 11 = 957인데 왜냐하면 8 + 7 = 15이므로 5는 8과 7 사이에 가고 1은 8에 올려지기 때문입니다. 따라서 기본적으로 857 + 100 = 957입니다.
Multiplying two 2 digit numbers between 11 and 19
11과 19 사이의 2 자리 숫자를 쉽게 곱하기 위한 간단한 알고리듬은 다음과 같습니다 (여기서 a는 첫 번째 숫자의 일 자리이고 b는 두 번째 숫자의 일 자리입니다):
(10+a)×(10+b)
100 + 10×(a+b) + a×b
이것은 더해져야 할 세 부분으로 시각화될 수 있습니다:
1
xx
yy
예를 들어:
17×16
1 = 100
13 (7+6) = 10×(a+b)
42 (7×6) = a×b
272 (total)
Using hands: 6–10 multiplied by another number 6–10
이 기법은 6에서 10까지의 숫자를 6에서 10까지의 또 다른 숫자에 곱해지는 것을 허용합니다.
소지에 6, 약지에 7, 중지에 8, 검지에 9, 엄지에 10을 할당합니다. 두 원했던 숫자를 함께 터치합니다. 접촉 지점과 그 아래는 "아래쪽" 섹션으로 고려되고 접촉하는 두 손가락 위의 모든 것은 "위쪽" 섹션의 일부입니다. 답은 왼손 및 오른손 "위쪽" 손가락의 숫자의 곱에 "아래쪽" 손가락 총 숫자의 열 배를 더하여 형성됩니다.
예를 들어, 9 × 6는 오른쪽 소지에 접촉하는 왼쪽 검지와 함께 다음처럼 보일 것입니다:
=10== :오른쪽 엄지 (위쪽)
==9== :오른쪽 검지 (위쪽)
==8== :오른쪽 중지 (위쪽)
왼쪽 엄지: =10== ==7== :오른쪽 약지 (위쪽)
왼쪽 검지: --9---><---6-- :오른쪽 소지 (아래쪽)
왼쪽 중지: --8-- (아래쪽)
왼쪽 약지: --7-- (아래쪽)
왼쪽 소지: --6-- (아래쪽)
이 예제에서, 5 "아래쪽" 손가락 (왼쪽 검지, 중지, 약지, 및 소지, 더하기 오른쪽 소지), 1 왼쪽 "위쪽" 손가락 (왼쪽 엄지), 및 4 오른쪽 "위쪽" 손가락 (오른쪽 엄지, 검지, 중지, 및 소지)가 있습니다. 따라서 계산은 다음처럼 됩니다:
9 × 6 = (10 × 5) + (1 × 4) = 54.
또 다른 예제, 8 × 7를 생각해 보십시오:
=10== :오른쪽 엄지 (위쪽)
왼쪽 엄지: =10== ==9== :오른쪽 검지 (위쪽)
왼쪽 검지: ==9== ==8== :오른쪽 중지 (위쪽)
왼쪽 중지: --8---><---7-- :오른쪽 약지 (아래쪽)
왼쪽 약지: --7-- --6-- :오른쪽 소지 (아래쪽)
왼쪽 소지: --6-- (아래쪽)
다섯 아래쪽 손가락은 5 십, 또는 50을 만듭니다. 두 위쪽 왼쪽 손가락과 셋 위쪽 오른쪽 손가락은 곱 6을 만듭니다. 이들을 합하면 답, 56을 산출합니다.
또 다른 예제, 이번에는 6 × 8:
--8---><---6--
--7--
--6--
넷의 십 (아래쪽), 더하기 이 곱하기 사 (위쪽)은 40 + 2 × 4 = 48을 제공합니다.
여기에 그것이 작동하는 방법입니다: 각 손가락은 6에서 10 사이의 숫자를 나타냅니다. 우리가 x와 y를 나타내는 손가락들을 결합할 때, 왼쪽 손에 10 − x "위쪽" 손가락과 x − 5 "아래쪽" 손가락이 있습니다; 오른쪽 손에 10 − y "위쪽" 손가락과 y − 5 "아래쪽" 손가락이 있습니다.
다음이라고 놓습니다:
\(\quad\displaystyle \, t_L = 10 - x \,\) (왼쪽 손에 "위쪽" 손가락의 숫자)
\(\quad\displaystyle \, t_R = 10 - y \,\) (오른쪽 손에 "위쪽" 손가락의 숫자)
\(\quad\displaystyle \, b_L = x - 5 \,\) (왼쪽 손에 "아래쪽" 손가락의 숫자)
\(\quad\displaystyle \, b_R = y - 5 \,\) (오른쪽 손에 "아래쪽" 손가락의 숫자)
그런-다음 위의 지침을 따르면 다음을 생산합니다:
\(\quad\displaystyle \, 10 (b_L + b_R) + t_L t_R\)
\(\quad\displaystyle \, =10[(x-5)+(y-5)] + (10-x)(10-y)\)
\(\quad\displaystyle \, =10(x+y-10) + (100-10x-10y+xy)\)
\(\quad\displaystyle \, =[10(x+y) - 100] + [100 - 10(x+y) + xy]\)
\(\quad\displaystyle \, =[10(x+y)-10(x+y)] + [100-100] + xy\)
\(\quad\displaystyle \, =xy \)
이것이 원했던 곱입니다.
Multiplying two numbers close and below 100
이 기법은 100에 가깝고 작은 숫자 (90-99)를 쉬운 곱셈을 허용합니다. 변수는 곱하는 두 숫자가 됩니다.
90-99 범위의 두 변수의 곱은 4-자리 숫자를 초래할 것입니다. 첫 번째 단계는 일-자리와 십 자리를 찾기 위한 것입니다.
100에서 변수 둘 다를 빼면 2 일-자리 숫자를 초래할 것입니다. 2 일-자리 숫자의 곱은 최종 곱의 마지막 두 자리일 것입니다.
다음으로, 100에서 두 변수 중 하나를 뺍니다. 그런-다음 다른 변수에서 차이를 뺍니다. 해당 차이는 최종 곱의 처음 두 자리가 될 것이고, 결과 4 자리 숫자가 최종 곱이 될 것입니다.
예제:
95
x 97
----
마지막 두 자리: 100-95=5 (100에서 첫 번째 숫자를 뺍니다)
100-97=3 (100에서 두 번째 숫자를 뺍니다)
5*3=15 (두 차이를 곱합니다)
최종 곱- yx15
처음 두 자리: 100-95=5 (100에서 첫 번째 숫자를 뺍니다)
97-5=92 (방정식의 두 번째 숫자에서 해당 답을 뺍니다)
이제, 차이는 처음 두 자릿수일 것입니다
최종 곱- 9215
처음 두 자릿수에 대해 대안
5+3=8 (이전 단계에서 "마지막 두 자릿수"를 계산할 때 유도된 두 단일 자릿수를 더합니다)
100-8=92 (100에서 해당 답을 뺍니다)
이제, 차이가 처음 두 자릿수일 것입니다
최종 곱- 9215
Using square numbers
작은 숫자의 곱은 정수의 제곱을 사용함으로써 계산될 수 있습니다; 예를 들어 13 × 17을 계산하기 위해, 우리는 15가 두 인수의 평균임을 언급하고, 그것을 (15 − 2) × (15 + 2), 즉 \(15^2-2^2\)로 생각할 수 있습니다. \(15^2\)는 225이고 \(2^2\)임을 알고 있으며, 단순한 뺄셈이 원하는 곱인 225 − 4 = 221임을 보여줍니다.
이 방법은 특정 숫자의 제곱을 암기해서 알고 있어야 함을 요구합니다:
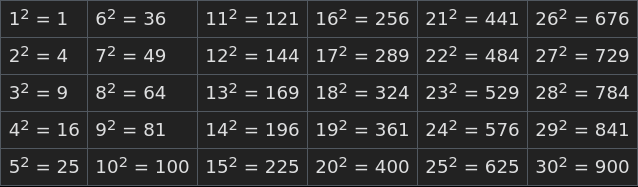
Squaring numbers
두 연속된 제곱 숫자의 차이는 그들 각각의 제곱근의 합이라는 것을 아는 것이 유용할 수 있습니다. 그러므로, 만약 우리가 12 × 12 = 144를 알고 13 × 13을 알고 싶다면, 144 + 12 + 13 = 169를 계산합니다.
이것은 \((x+1)^2-x^2 = x^2+2x+1-x^2= x+(x+1)\) 또는 \(x^2=(x-1)^2+(2x-1)\)이기 때문입니다.
Squaring any number
주어진 숫자를 취하고, 그것에 특정 값을 더하고 빼면 더 쉽게 곱할 수 있습니다. 예를 들어:
\(\quad 492^2\)
492는 500에 가까워, 곱하는 것이 쉽습니다. 다음을 얻기 위해 8 (500과 492 사이의 차이)을 더하고 뺍니다:
\(\quad 492 \rightarrow 484, 500\)
이 숫자를 함께 곱하면 242,000를 얻습니다 (이것은 484를 2로 나누어 242를 얻고 1000을 곱함으로써 효율적으로 행해질 수 있습니다). 마지막으로, 다음 결과를 얻기 위해 차이 (8) 제곱 (\(8^2=64\))를 더합니다:
\(\quad 492^2 = 242,064\)
증명은 다음과 같습니다:
\(\quad\displaystyle n^2 = n^2\)
\(\quad\displaystyle n^2 = (n^2 - a^2) + a^2\)
\(\quad\displaystyle n^2 = (n^2 - an + an - a^2) + a^2\)
\(\quad\displaystyle n^2 = (n-a)(n+a) + a^2\)
Squaring any 2-digit integer
이 방법은 한-자리 숫자 1에서 9까지의 제곱의 암기를 요구합니다.
mn의 제곱은, mn이 두-자리 정수이며, 다음처럼 계산될 수 있습니다:
\(\quad 10 \times m(mn+n)+n^2\)
mn의 제곱은 mn에 n을 더하고, m을 곱하고, 그런-다음 끝에 0을 더하고 마지막으로 n의 제곱을 더하여 구해질 수 있음을 의미합니다.
예를 들어, \(23^2\):
\(\quad 23^2 = 10 \times 2(23+3) + 3^2\)
\(\quad = 10 \times 2(26) + 9\)
\(\quad = 520+9\)
\(\quad =529\)
따라서 \(23^2=529\).
Squaring a number ending in 5
- 5 앞에 오는 숫자를 가져옵니다: abc5, 여기서 a, b, c는 자릿수입니다.
- 이 숫자와 자체에 1을 더한 값에 곱합니다 : abc(abc + 1)
- 위의 결과를 취하고 끝에 25를 부착합니다.
- 예제: 85 × 85
- 8
- 8 × 9 = 72
- 따라서, \(85^2=7,225\)
- 예제: \(125^2\)
- 12
- 12 × 13 = 156
- 따라서, \(125^2=15,625\)
- 수학적 표현
- 예제: 85 × 85
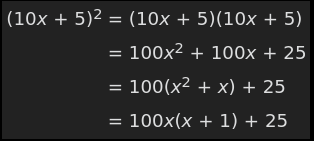
Squaring numbers very close to 50
50에 가까운 숫자 n을 제곱해야 한다고 가정합니다.
숫자는 n = 50 − a로 표현될 수 있으므로 그것의 제곱은 \((50-a)^2=50^2-100a + a^2\)입니다. 우리는 \(50^2\)가 2500이라는 것을 알고 있습니다. 따라서 우리는 2500에서 100a를 빼고, 그런-다음 \(a^2\)을 더합니다.
예제, 말하자면 우리가 48을 제곱하고 싶은데, 이것은 50 − 2입니다. 우리는 2500에서 200을 빼고 4를 더하고, \(n^2=2304\)를 얻습니다. 50 (n = 50 + a)보다 더 큰 숫자에 대해, 빼는 대신에 100×a를 더합니다.
Squaring an integer from 26 to 74
이 방법은 1에서 24까지의 제곱의 암기를 요구합니다.
n의 제곱은 다음입니다 (n이 26에서 74 사이일 때 가장 쉽게 계산됩니다):
\(\quad (50-n)^2+100(n-25)\)
다시 말해서, 숫자의 제곱은 50으로부터 그것의 차이의 제곱에 숫자와 25의 차이를 100배 한 것을 더한 것입니다. 예를 들어, 62를 제곱하기 위해:
\(\quad (-12)^2+[(62-25)] \times 100]\)
\(\quad = 144+3,700\)
\(\quad = 3,844\)
Squaring an integer near 100 (e.g., from 76 to 124)
이 방법은 1에서 a까지의 제곱의 암기를 요구하며, 여기서 a는 n과 100 사이의 절대 차이입니다. 예를 들어, 1에서 24까지의 제곱을 암기한 학생들은 76에서 124까지의 임의의 정수에 이 방법을 적용할 수 있습니다.
n (즉, 100 ± a)의 제곱은 다음입니다:
\(\quad 100(100\pm 2a) + a^2\)
다시 말해서, 숫자의 제곱은 100으로부터 그것의 차이의 제곱에 2와 백과 그 숫자의 차이를 곱하고, 100에서 그 결과의 차이를 100과 곱한 것을 더한 것입니다. 예를 들어, 93을 제곱하기 위해:
\(\quad 100(100-2(7))+7^2\)
\(\quad = 100 \times 86 + 49\)
\(\quad = 8,600+49\)
\(\quad = 8,649\)
그것을 보는 또 다른 방법은 다음과 같습니다:
\(\quad 93^2 = ?\) (100으로부터 −7입니다)
\(\quad 93-7 =86\) (이것은 처음 두 자릿수를 제공합니다)
\(\quad (-7)^2=49\) (이것들은 두 번째 두 자릿수입니다)
\(\quad 93^2=8649\)
또 다른 예제:
822 = ? (100으로부터 −18입니다)
82 − 18 = 64 (빼서, 처음 자릿수.)
(−18)2 = 324 (두 번째 자릿수의 쌍. 우리는 3을 올려야 합니다.)
822 = 6724
Squaring any integer near \(10^n\) (e.g., 976 to 1024, 9976 to 10024, etc.)
이 방법은 100에 가까운 정수를 제곱하기 위해 위에 주어진 설명의 간단한 확장입니다.
Squaring any integer near \(m \times 10^n\) (e.g., 276 to 324, 4976 to 5024, 79976 to 80024)
이 방법은 \(10^n\)에 가까운 정수에 대해 위에 제공된 설명의 간단한 확장입니다.
Finding roots
Approximating square roots
숫자의 제곱근(square root)을 근사하기 위한 쉬운 방법은 다음 방정식을 사용하는 것입니다:
\(\quad\displaystyle \text{root }\simeq\text{ known square root} - \frac{\text{known square} - \text{unknown square}}{2 \times \text{known square root}}\,\)
알려진 제곱(square)이 알려지지 않은 것에 가까울수록, 더 정확한 근사입니다. 예를 들어, 15의 제곱 근을 추정하기 위해, 우리는 가장 가까운 완전 제곱이 16 (\(4^2\))이라는 지식으로 시작할 수 있습니다.
\(\quad\displaystyle \begin{align}
\text{root} & \simeq 4 - \frac{16 - 15}{2 \times 4} \\
& \simeq 4 - 0.125 \\
& \simeq 3.875 \\
\end{align}\,\!
\)
따라서 15의 추정된 제곱 근은 3.875입니다. 15의 실제 제곱 근은 3.872983...입니다. 한 가지 주목할 것은 원래 추측이 무엇이든지, 추정된 답은 산술과 기하 평균의 부등식(inequality of arithmetic and geometric means)으로 인해 항상 실제 답보다 더 커질 것이라는 점입니다. 따라서, 우리는 추정된 답을 반내림해야 합니다.
만약 \(n^2\)이 원했던 제곱 x에 가장 가까운 완전 제곱이고 \(d=x-n^2\)이 그 차이이면, 이 근사를 \(\displaystyle n\tfrac{d}{2n}\)으로 혼합된 분수의 형식으로 표현하는 것이 더 편리함에 주목하십시오. 따라서, 이전 예제에서, 15의 제곱근은 \(\displaystyle 4\tfrac{-1}{8}\)입니다. 또 다른 예제로서, 41의 제곱근은 \(\displaystyle 6\tfrac{5}{12} = 6.416\)이지만 실제 값은 6.4031...입니다.
Derivation
정의에 의해, 만약 r이 x의 제곱 근이면, 다음입니다:
\(\quad\displaystyle \mathrm{r}^2 = x\,\!\)
우리는 그런-다음 다음으로 근을 다시-정의합니다:
\(\quad\displaystyle \mathrm{r} = a - b\,\!\)
여기서 a는 알려진 근 (위의 예제에서 4)이고 b는 알려진 근과 우리가 찾는 답 사이의 차이입니다.
\(\quad\displaystyle (a-b)^2 = x\,\!\)
전개하면 다음을 산출합니다:
\(\quad\displaystyle a^2 - 2ab + b^2 = x\,\!\)
만약 'a'가 대상에 가까우면, b는 방정식의 \(\displaystyle {} + b^2\,\) 요소를 무시할 수 있을 만큼 충분히 작을 것입니다. 따라서 우리는 \(\displaystyle {} + b^2\,\)를 버리고 방정식을 다음과 같이 다시-정리할 수 있습니다:
\(\quad\displaystyle b \simeq \frac{a^2 - x}{2a}\,\!\)
따라서
\(\quad\displaystyle \mathrm{root} \simeq a - \frac{a^2 - x}{2a}\,\!\)
이것은 다음으로 추론될 수 있습니다:
\(\quad\displaystyle \mathrm{root} \simeq \frac{a^2 + x}{2a}\,\!\)
Extracting roots of perfect powers
완전 거듭제곱(perfect powers)의 근을 추출하는 것은 종종 실행됩니다. 과제의 난이도는 완전 거듭제곱의 자릿수에 의존하지 않고 정밀도, 즉 근의 자릿수의 숫자에 의존합니다. 게다가, 그것은 역시 근의 순서에 따라 다릅니다; 다음 섹션에서와 같이, 자릿수가 일관된 방법으로 나오기 때문에 근의 순서가 10과 서로소(coprime)인 완전 근을 찾는 것이 다소 쉽습니다.
Extracting cube roots
초보자를 위한 쉬운 작업은 2 자리 숫자의 세제곱으로부터 세제곱 근을 추출하는 것입니다. 예를 들어, 74088이 주어지면, 자체를 한 번 곱하고 그런-다음 다시 숫자를 곱했을 때, 74088을 산출하는 두 자리 숫자가 무엇인지를 결정합니다. 방법을 아는 사람은 \(42^3=74088\)과 같이 답이 42라는 것을 금방 알 것입니다.
절차를 배우기 전에, 수행자는 숫자 1-10의 세제곱을 암기하는 것을 요구합니다:
맨 오른쪽 숫자에 패턴이 있는지 관찰하십시오: 1 또는 3으로 더하고 빼십시오. 영에서 시작하여:
두 자리 숫자의 세제곱에서 세제곱 근을 추출하는 두 단계가 있습니다. 예를 들어, 29791의 세제곱 근을 추출합니다. 두 자리 숫자의 일의 위치 (단위)를 결정합니다. 위와 보이는 것처럼, 세제곱이 1로 끝나므로, 그것은 1이어야 합니다.
- 만약 완전 세제곱이 0으로 끝나면, 그것의 세제곱 근은 0으로 끝나야 합니다.
- 만약 완전 세제곱이 1으로 끝나면, 그것의 세제곱 근은 1으로 끝나야 합니다.
- 만약 완전 세제곱이 2으로 끝나면, 그것의 세제곱 근은 8으로 끝나야 합니다.
- 만약 완전 세제곱이 3으로 끝나면, 그것의 세제곱 근은 7으로 끝나야 합니다.
- 만약 완전 세제곱이 4으로 끝나면, 그것의 세제곱 근은 4으로 끝나야 합니다.
- 만약 완전 세제곱이 5으로 끝나면, 그것의 세제곱 근은 5으로 끝나야 합니다.
- 만약 완전 세제곱이 6으로 끝나면, 그것의 세제곱 근은 6으로 끝나야 합니다.
- 만약 완전 세제곱이 7으로 끝나면, 그것의 세제곱 근은 3으로 끝나야 합니다.
- 만약 완전 세제곱이 8으로 끝나면, 그것의 세제곱 근은 2으로 끝나야 합니다.
- 만약 완전 세제곱이 9으로 끝나면, 그것의 세제곱 근은 9으로 끝나야 합니다.
모든 각 자릿수는 2, 3, 7과 8을 제외하고 자체 숫자에 해당하며, 이것들은 단지 십에서 해당 자릿수를 얻기 위해 빼는 것에 주목하십시오.
두 번째 단계는 주어진 세제곱의 크기를 봄으로써 두 자리 세제곱 근의 첫 번째 자릿수를 결정하는 것입니다. 이것을 하기 위해, 주어진 세제곱의 마지막 세 자릿수 (29791 → 29)를 제거하고 그것보다 더 큰 가장 큰 세제곱을 찾습니다 (이것은 숫자 1-10의 세제곱을 아는 것이 요구되는 곳입니다). 여기서, 29는 1 세제곱보다 더 크고, 2 세제곱보다 크고, 3 세제곱보다 더 크지만, 4 세제곱보다 더 크지는 않습니다. 가장 큰 세제곱은 3보다 크므로, 두 자리 세제곱의 첫 번째 자릿수는 3이어야 합니다.
그러므로, 29791의 세제곱 근은 31입니다.
또 다른 예제:
- 456533의 세제곱 근을 찾습니다.
- 세제곱 근은 7로 끝납니다.
- 마지막 세 자릿수가 제거되고 난 후, 456이 남습니다.
- 456은 7 세제곱까지 모든 세제곱보다 더 큽니다.
- 세제곱 근의 처음 자릿수는 7입니다.
- 456533의 세제곱 근은 77입니다.
이 과정은 산술 모듈로 11을 사용함으로써 3 자릿수 길이인 세제곱 근을 찾기 위해 확장될 수 있습니다.
이러한 유형의 트릭은 근의 순서가 10과 서로소인 임의의 근에서 사용될 수 있습니다; 따라서 그것은 제곱 근에서 작동에 실패하는데, 왜냐하면 거듭제곱, 2는 10으로 나뉘기 때문입니다. 3은 10을 나누지 않고, 따라서 세제곱 근이 작동합니다.
Approximating common logarithms (log base 10)
상용 로그 (적어도 한 십진 점 정확도에서)를 근사하기 위해, 몇 가지 로그 규칙과 몇 개의 로그를 암기가 요구됩니다. 우리는 다음 사항을 알아야 합니다:
- log(a × b) = log(a) + log(b)
- log(a / b) = log(a) - log(b)
- log(0)는 존재하지 않습니다.
- log(1) = 0
- log(2) ~ .30
- log(3) ~ .48
- log(7) ~ .85
이 정보로부터, 우리는 임의의 숫자 1-9의 로그를 찾을 수 있습니다.
- log(1) = 0
- log(2) ~ .30
- log(3) ~ .48
- log(4) = log(2 × 2) = log(2) + log(2) ~ .60
- log(5) = log(10 / 2) = log(10) − log(2) ~ .70
- log(6) = log(2 × 3) = log(2) + log(3) ~ .78
- log(7) ~ .85
- log(8) = log(2 × 2 × 2) = log(2) + log(2) + log(2) ~ .90
- log(9) = log(3 × 3) = log(3) + log(3) ~ .96
- log(10) = 1 + log(1) = 1
공통 로그를 근사화하는 첫 번째 단계는 과학적 표기법으로 주어진 숫자를 넣는 것입니다. 예를 들어, 과학적 표기법에서 숫자 45는 \(4.5 \times 10^1\)이지만, 우리는 그것을 \(a \times 10^b\)라고 부를 것입니다. 다음으로, 1과 10 사이에 있는 a의 로그를 찾습니다. 먼저 4의 로그, .60를 찾음으로써 시작하고, 5의 로그, .70를 찾는데, 왜냐하면 4.5는 이들 둘 사이에 있기 때문입니다. 다음으로, 그리고 여기에서 기술은 연습과 함께 제공되며, .6과 .7 사이의 로그 스케일로 .653 어딘가에 5를 배치합니다 (참고: 여분의 위치의 실제 값은 항상 만약 그것이 정규 스케일에 배치되면 더 클 것이며, 즉, 우리가 그것이 절반이기 때문에 .650에서 갈 것으로 예상할 수 있으면 대신 그것이 약간 더 클 것이며, 이 경우에서 .653입니다) 한 번 우리가 a의 로그를 얻었으면, 단순히 그것에 b를 다하여 상용 로그의 근사를 얻습니다. 이 경우에서, a + b = .653 + 1 = 1.653입니다. 실제 값은 log(45) ~ 1.65321입니다.
같은 과정은 0과 1 사이의 숫자에 적용합니다. 예를 들어, 0.045는 \(4.5 \times 10^{-2}\)로 표시됩니다. 유일한 차이점은 b는 이제 음수이므로, 일을 더하는 것은 실제로 빼는 것입니다. 이것은 결과 0.653 − 2, 또는 −1.347을 산출합니다.
Mental arithmetic as a psychological skill
적절한 수준의 육체적 노력(physical exertion)은 나중에 수행되는 암기 계산을 행하는 것과 같은 정신 직무(mental task)의 수행에서 증가로 이어질 수 있습니다. 높은 수준의 신체적 활동 동안 정신 직무 수행에 부정적인 영향이 있음이 밝혀져 왔습니다. 이것은 너무 많은 육체 노동이 암기 수학 계산의 정확도와 출력을 떨어뜨릴 수 있음을 의미합니다. 생리학적(Physiological) 측정, 특히 EEG는 정신적 작업량(mental workload)을 나타내는 데 유용한 것으로 나타났습니다. 다양한 수준의 육체적 활동 후 정신적 작업량의 측정으로 EEG를 사용하면 정신적 수행에 가장 유익한 신체 활동 수준을 결정하는 데 도움이 될 수 있습니다. 란자나 메타(Ranjana Mehta)에 의해 미시간 공과 대학(Michigan Technological University)에서 행해진 이전 연구는 동시에 정신적, 육체적 작업에 참여한 참가자들을 포함했었던 최근 연구를 포함합니다. 이 연구는 다양한 수준의 육체적 노력에서 신체적 수행에 요구되는 정신의 영향을 조사했고 궁극적으로 정신적 작업이 동시에 완료될 때, 육체적 작업량의 더 높은 수준에서 보다 중요한 효과(significant effect)를 갖는 신체적 수행에서 감소를 찾았습니다. 브라운–피터슨 절차(Brown–Peterson procedure)는 암기 산술을 사용하는 널리 알려진 작업입니다. 주로 인지(cognitive) 실험에 사용되는, 이 절차는 유지 암송(maintenance rehearsal)이 단기 기억(short-term memory)이 얼마나 오래 지속되는지에 대한 효과를 테스트하는 것에 정신적 뺄셈이 유용함을 제안합니다.
Mental Calculations World Championship
첫 번째 암기 계산 세계 대회(Mental Calculations World Championship)가 1997년에 열렸습니다. 이 이벤트는 매년 반복됩니다. 그것은 열-자리 숫자의 덧셈, 두 여덟-자리 숫자의 곱셈, 제곱근의 계산, 주어진 날짜에 대한 평일의 계산, 세제곱근 계산, 및 일부 놀라운 잡다한 임무와 같은 다양한 임무로 구성됩니다.
Mental Calculation World Cup
첫 번째 세계 암기 계산 대회 (암기 계산 월드컵)는 2004년에 열렸습니다. 그것들은 2년마다 반복됩니다. 그것은 여섯 다른 임무: 열-자리 숫자의 덧셈, 두 여덟-자리 숫자의 곱셈, 제곱근의 계산, 및 주어진 날짜에 대한 평일의 계산, 세제곱근 계산 및 일부 놀라운 잡다한 임무로 구성됩니다.
Memoriad – World Memory, Mental Calculation & Speed Reading Olympics
Memoriad는 "암기 계산", "기억" 및 "사진 읽기" 대회를 결합한 최초의 플랫폼입니다. 게임과 대회는 올림픽이 열리는 해에 매 4년마다 열립니다. 첫 번째 Memoriad는 2008년 터키(Turkey), 이스탄불(Istanbul)에서 열렸습니다. 두 번째 Memoriad는 2012년 11월 24–25일에 터키, 안탈리아(Antalya)에서 열렸습니다. 20개국에서 89명이 참가했습니다. 상과 상금이 전체에서 10 카테고리에 대해 주어졌습니다; 그것의 5 카테고리가 암기 계산(Mental Calculation) (암기 덧셈, 암기 곱셈, 암기 제곱근 (비-정수), 암기 달력 날짜 계산과 Flash Anzan)에 대해 수행되어야 합니다.
External links
- Mental Calculation World Cup
- Memoriad - World Mental Olympics
- Tzourio-Mazoyer, Nathalie; Pesenti, Mauro; Zago, Laure; Crivello, Fabrice; Mellet, Emmanuel; Samson, Dana; Duroux, Bruno; Seron, Xavier; Mazoyer, Bernard (2001). "Mental calculation in a prodigy is sustained by right prefrontal and medial temporal areas". Nature Neuroscience. 4 (1): 103–7. doi:10.1038/82831. PMID 11135652.
- Rivera, S.M.; Reiss, AL; Eckert, MA; Menon, V (2005). "Developmental Changes in Mental Arithmetic: Evidence for Increased Functional Specialization in the Left Inferior Parietal Cortex". Cerebral Cortex. 15 (11): 1779–90. doi:10.1093/cercor/bhi055. PMID 15716474.
- Large EEG waves ellicited by Mental Calculation PDF
- Mathletics - train or compete in Mental Math
- Mathematical Shortcuts from Vedic Maths
