
기하학(geometry)에서, 삼각형(triangle)의 중앙선은 꼭짓점(vertex)을 반대쪽 변의 중간점(midpoint)에 연결하는 선분(line segment)이며, 따라서 해당 변을 이등분합니다. 모든 각 삼각형은 각 꼭짓점에서 하나씩 정확하게 셋의 중앙선이 있고, 그것들 모두는 삼각형의 도형중심(centroid)에서 서로 교차합니다. 이등변(isosceles) 삼각형과 등변(equilateral) 삼각형에 대해, 중앙선은 둘의 인접한 변이 길이에서 같은 꼭짓점에서 임의의 각도를 이등분합니다.
중앙선의 개념은 사면체(tetrahedra)까지 확장됩니다.
Relation to center of mass
삼각형의 각 중앙선은 삼각형의 도형중심(centroid)을 통과하며, 이것은 삼각형과 일치하는 균등 밀도의 무한하게 얇은 물체의 질량의 중심(center of mass)입니다. 따라서 물체는 중앙선의 교차점에서 균형을 이룰 것입니다. 도형중심은 중앙선이 나오는 꼭짓점보다 중앙선이 교차하는 변의 중앙선을 따라 두 배 더 가깝습니다.
Equal-area division
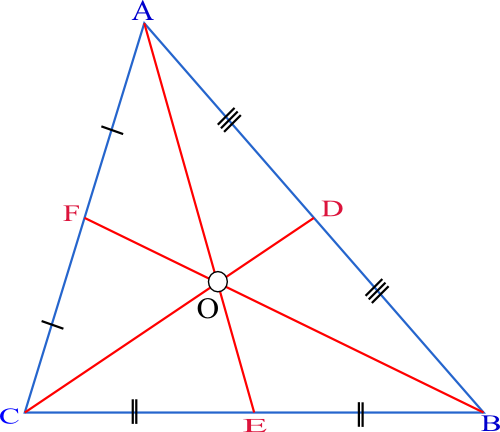
각 중앙선은 삼각형의 넓이를 반으로 나눕니다; 그러므로 그 이름이고 따라서 균등 밀도의 삼각형 물체는 임의의 중앙선에서 균형을 이룰 것입니다. (삼각형의 넓이를 같은 두 부분으로 나누는 임의의 다른 직선은 도형중심을 통과하지 않습니다.) 셋의 중앙선은 삼각형을 같은 넓이(area)의 여섯의 더 작은 삼각형으로 나눕니다.
Proof of equal-area property
삼각형 ABC를 생각해 보십시오. D를 \(\overline{AB}\)의 중간점, E를 \(\overline{BC}\)의 중간점, F를 \(\overline{AC}\)의 중간점으로 놓고, O를 도형중심으로 놓습니다 (대부분 공통적으로 G로 표시됨).
정의에 의해, \(AD=DB, AF=FC, BE=EC \)입니다. 따라서 \([ADO]=[BDO], [AFO]=[CFO], [BEO]=[CEO],\) 및 \([ABE]=[ACE] \)이며, 여기서 \([ABC]\)는 삼각형 \(\triangle ABC\)의 넓이(area)를 나타냅니다; 이것들은 유지되는데 왜냐하면 각 경우에서 두 삼각형은 같은 길이의 밑변을 가지고 (연장된) 밑변으로부터 공통 고도를 공유하고, 삼각형의 넓이는 밑변 곱하기 높이의 절반과 같기 때문입니다.
우리는 다음을 가집니다:
\(\quad\)\([ABO]=[ABE]-[BEO] \)
\(\quad\)\([ACO]=[ACE]-[CEO] \)
따라서, \([ABO]=[ACO] \)이고 \([ADO]=[DBO], [ADO]=\frac{1}{2}[ABO]\)입니다.
\([AFO]=[FCO], [AFO]= \frac{1}{2}[ACO]=\frac{1}{2}[ABO]=[ADO]\)이기 때문에, 따라서, \([AFO]=[FCO]=[DBO]=[ADO]\)입니다. 같은 방법을 사용하여, 우리는 \([AFO]=[FCO]=[DBO]=[ADO]=[BEO]=[CEO] \)임을 보일 수 있습니다.
Three congruent triangles
2014년 리 샐로즈(Lee Sallows)는 다음 정리를 발견했습니다:
임의의 삼각형의 중앙선은 삼각형의 세 개의 인접한 쌍이 중간점 D, E, 및 F에서 만나는 위의 그림과 같이 여섯의 같은 넓이 더 작은 삼각형으로 분할합니다. 만약 그러한 각 쌍에서 두 삼각형이 공통 변을 공유하도록 만날 때까지 공통 중간점을 중심으로 회전하면, 각 쌍의 합집합에 의해 형성된 셋의 새로운 삼각형은 합동입니다.
Formulas involving the medians' lengths
중앙선의 길이는 아폴로니우스의 정리(Apollonius' theorem)에서 다음과 같이 얻어질 수 있습니다:
\(\quad\)\(\displaystyle m_a = \sqrt{\frac{2 b^2 + 2 c^2 - a^2}{4}}\)
\(\quad\)\(\displaystyle m_b = \sqrt{\frac{2 a^2 + 2 c^2 - b^2}{4}}\)
\(\quad\)\(\displaystyle m_c = \sqrt{\frac{2 a^2 + 2 b^2 - c^2}{4}}\)
여기서 \(a, b,\) 및 \(c\)는 그들 중간점에서 각각 중앙선 \(m_a, m_b,\) 및 \(m_c\)를 갖는 삼각형의 변입니다.
이들 공식은 다음 관계를 의미합니다:
\(\quad\)\(\displaystyle a = \frac{2}{3} \sqrt{-m_a^2 + 2m_b^2 + 2m_c^2} = \sqrt{2(b^2+c^2)-4m_a^2} = \sqrt{\frac{b^2}{2} - c^2 + 2m_b^2} = \sqrt{\frac{c^2}{2} - b^2 + 2m_c^2}\)
\(\quad\)\(\displaystyle b = \frac{2}{3} \sqrt{-m_b^2 + 2m_a^2 + 2m_c^2} = \sqrt{2(a^2+c^2)-4m_b^2} = \sqrt{\frac{a^2}{2} - c^2 + 2m_a^2} = \sqrt{\frac{c^2}{2} - a^2 + 2m_c^2}\)
\(\quad\)\(\displaystyle c = \frac{2}{3} \sqrt{-m_c^2 + 2m_b^2 + 2m_a^2} = \sqrt{2(b^2+a^2)-4m_c^2} = \sqrt{\frac{b^2}{2} - a^2 + 2m_b^2} = \sqrt{\frac{a^2}{2} - b^2 + 2m_a^2}.\)
Other properties
ABC를 삼각형으로 놓고, G를 그것의 도형중심으로 놓고, D, E, 및 F를 각각 BC, CA, 및 AB의 중간점으로 놓습니다. ABC의 평면에서 임의의 점 P에 대해, 그런-다음
\(\quad\)\(PA+PB+PC \leq 2(PD+PE+PF) + 3PG.\)
도형중심은 각 중앙선을 2:1 비율에서 부분으로 나누며, 도형중심은 반대쪽 꼭짓점보다 변의 중간점에 두 배 가깝습니다.
변 \(a, b, c\)와 중앙선 \(m_a, m_b, m_c\)를 갖는 임의의 삼각형에 대해,
\(\quad\)\(\tfrac{3}{4}(a+b+c) < m_a + m_b + m_c < a+b+c \quad \text{ and } \quad \tfrac{3}{4}\left(a^2+b^2+c^2\right) = m_a^2 + m_b^2 + m_c^2.\)
길이 \(a\)와 \(b\)의 변으로부터 중앙선이 수직(perpendicular)인 것과 \(a^2 + b^2 = 5c^2\)이 것은 필요충분 조건입니다.
빗변 \(c\)를 갖는 직각 삼각형(right triangle)의 중앙선은 \(m_a^2 + m_b^2 = 5m_c^2\)를 만족시킵니다.
임의의 삼각형의 넓이 T는 다음처럼 그것의 중앙선 \(m_a, m_b\), 및 \(m_c\)의 관점에서 표현될 수 있습니다. 만약 그것들의 반-합 \(\left(m_a + m_b + m_c\right)/2\)이 \(\sigma\)에 의해 표시되면, 다음입니다:
\(\quad\)\(\displaystyle T = \frac{4}{3} \sqrt{\sigma \left(\sigma - m_a\right)\left(\sigma - m_b\right)\left(\sigma - m_c\right)}.\)
Tetrahedron

사면체(tetrahedron)는 넷의 삼각형 면(faces)을 가진 삼-차원(three-dimensional) 물체입니다. 사면체의 꼭짓점과 반대쪽 면의 도형중심(centroid)을 연결하는 선분은 사면체의 중앙선이라고 불립니다. 넷의 중앙선이 있고, 그것들은 모두 사면체의 도형중심에서 공점(concurrent)입니다. 이-차원 경우와 마찬가지로, 사면체의 도형중심이 질량의 중심(center of mass)입니다. 어쨌든, 이-차원의 경우와 달리 도형중심은 중앙선을 2:1 비율이 아니라 3:1 비율로 나눕니다 (코만디노의 정리(Commandino's theorem)).
External links
- The Medians at cut-the-knot
- Area of Median Triangle at cut-the-knot
- Medians of a triangle With interactive animation
- Constructing a median of a triangle with compass and straightedge animated demonstration
- Weisstein, Eric W. "Triangle Median". MathWorld.


