함수에서 함수의 정의에 대해서 알아보았습니다. 여기서는 함수 중에 특별한 경우의 함수에 대해 알아보겠습니다.
일대일함수
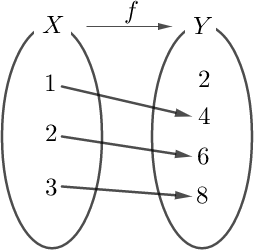
오른쪽 그림처럼 정의역 \(X=\{1,2,3\}\)와 공역 \(Y=\{2,4,6,8\}\)에 대하여 함수 \(f\colon X \to Y\)일 때, 집합 \(X\)의 각 원소에 집합 \(Y\)의 서로 다른 원소가 하나씩 대응됩니다. 이와 같이 정의역의 서로 다른 두 원소에 대응하는 공역의 원소가 서로 다른 원소를 갖는 함수를 일대일함수라고 합니다.
즉, 함수 \(f\colon X \to Y\)에서 정의역 \(X\)의 임의의 두 원소 \(x_1, x_2\)에 대하여
\(\quad\)\(x_1 \neq x_2 \implies f(x_1)\neq f(x_2)\)
일 때, 함수 \(f\)를 일대일함수라고 합니다.
한편 어떤 명제에 대해, 대우는 항상 진리값이 같으므로, 다음과 같이 역시 표현될 수 있습니다:
\(\quad\)\(f(x_1) = f(x_2) \implies x_1 = x_2\)
일대일 대응

오른쪽 그림처럼 정의역 \(X=\{1,2,3,4\}\)와 공역 \(Y=\{2,4,6,8\}\)에 대하여 함수 \(f\colon X \to Y\)일 때, 집합 \(X\)의 각 원소에 집합 \(Y\)의 서로 다른 원소가 하나씩 대응되고, 공역과 치역이 서로 같습니다. 이와 같이 공역과 치역이 같으며, 정의역의 서로 다른 두 원소에 대응하는 공역의 원소가 서로 다른 원소를 갖는 함수를 일대일 대응이라고 합니다.
즉, 함수 \(f\colon X \to Y\)에서 정의역 \(X\)의 임의의 두 원소 \(x_1, x_2\)에 대하여
\(\quad\)(1) 치역과 공역이 같고
\(\quad\)(2) \(x_1 \neq x_2 \implies f(x_1)\neq f(x_2)\) 일 때,
함수 \(f\)를 일대일 대응이라고 합니다.
일대일 대응의 그래프
함수의 그래프에서 \(y\)축과 나란한 직선과 한 곳에서 만날 때 \(f\colon X\to Y\)로의 함수임을 알아보았습니다.
한편, 함수 중에서 일대일의 그래프를 찾을 때에는 \(x\)축과 나란한 직선과 한 곳에서만 만나야 합니다. 즉, 정의역과 공역이 모든 실수일 때, 일대일 대응의 그래프는 다음과 같은 증가함수 또는 감소함수에서 나타납니다.
 |
 |
반면에 아래의 이차함수는 두 곳에서 만나기 때문에 일대일 대응이 아닙니다. 물론 정의역에 제한을 둔 이차함수는, 증가함수나 감소함수를 만들 수 있기 때문에, 일대일 대응이 가능합니다.
 |
 |
항등함수

오른쪽 그림처럼, 정의역의 임의의 원소에 대하여 그 함숫값이 자기 자신인 대응관계를 가질 때, 이와 같은 함수를 항등함수라고 합니다.
즉, 정의역의 임의의 원소에 대하여 함숫값이 자기 자신이 대응되는 함수
\(\quad\)\(f\colon X \to Y,\;f(x)=x\;(x\in X)\)
를 항등함수(identity function)라고 합니다.
상수함수

오른쪽 그림처럼, 정의역의 모든 원소에 대하여 그 함숫값이 항상 같은 값을 가지는 대응관계를 가질 때, 이와 같은 함수를 상수함수라고 합니다.
즉, 정의역 \(X\)의 모든 원소 \(x\)가 공역 \(Y\)의 한 원소에만 대응될 때,
\(\quad\)\(f\colon X \to Y,\;f(x)=c\;(c\in Y,\;c\)는 상수\()\)
를 상수함수라고 합니다.
상수함수의 그래프는 \(x\)축에 평행한 모든 직선이 이에 해당합니다.
응용예제
응용예제1
실수 전체에서 정의된 함수 \(f(x)=3|x-1|+ax+1\)의 역함수가 존재하기 위한 \(a\)의 범위는?
응용예제2
실수 전체의 집합에서 정의된 함수
\(\quad\)\(f(x)=\left\{\begin{align}
&ax+2 & (x \ge 0) \\
&(3-a)x+a & (x < 0)
\end{align}\right.\)
가 일대일함수가 되기 위한 실수 \(a\)의 값의 범위를 구하고, 그 풀이과정을 서술하시오.
응용예제3
실수 전체의 집합에서 정의된 함수
\(\quad\)\(f(x)=\left\{\begin{align}
& x^2-2ax+b & (x \ge 1) \\
& x-1 & (x<1)
\end{align}\right.\)
이 역함수가 존재하도록 하는 음이 아닌 실수 \(a,b\)에 대하여 점 \((a,b)\)의 자취의 길이가 \(\displaystyle \sqrt{\frac{q}{p}}\)일 때, \(p+q\)의 값을 구하시오. (단, \(p,q\)는 서로소인 자연수입니다.)
응용예제4
영이 아닌 임의의 실수 \(x\)에 대하여 \(f(x)\)가 \(\displaystyle f(x)+2f\left(\frac{1}{x}\right)=3x\)를 만족할 때, 방정식 \(f(x)=1\)의 두 근의 합을 구하여라.

