영문 위키피디아 번역

(번역) Quadrilateral

다움위키 2024. 3. 24. 02:40
Original article: w:Quadrilateral

 

유클리드 평면 기하학(Euclidean plane geometry)에서 사변형(quadrilateral)은 네 가장자리(edges) (변)와 네 꼭짓점(vertices) (구석)을 가진 다각형(polygon)입니다. 때때로, 용어 사각형(quadrangle)은 삼각형(triangle)과 아날로그에 의해 사용되고, 때때로 오각형(pentagon) (5-변) 및 육각형(hexagon) (6-변)과의 일관성을 위해 네모꼴(tetragon), 또는 k의 임의의 값에 대해 k-각과의 일관성을 위해 4-각(4-gon)을 사용합니다.

단어 "quadrilateral"은 라틴어 단어 quadri, 사의 변형, 및 "변"을 의미하는 latus로부터 파생됩니다.

사변형은 (자기-교차하지 않는) 단순(simple) 또는, 역시 교차된 것으로 불리는, (자기-교차하는) 복잡(complex)입니다. 단순 사변형은 볼록(convex) 또는 오목(concave)입니다.

단순 (및 평면) 사변형 ABCD의 내부 각도(interior angles)는 합해져서 360 호의 각도(degrees of arc)를 가집니다. 즉,

\(\quad\displaystyle \angle A+\angle B+\angle C+\angle D=360^{\circ}.\)

이것은 n-각 내부 각도 합 공식 (n − 2) × 180°의 특정 경우입니다.

모든 비-자기-교차하는 그들 가장자리의 중간-점을 중심으로 반복된 회전에 의해 평면을 타일링(tile the plane)합니다.

Simple quadrilaterals

자기 교차하지 않는 사변형은 단순한 사변형입니다.

Convex quadrilaterals

볼록 사변형에서, 모든 내부 각도는 180°보다 작고 두 대각선 둘 다는 사변형 안에 있습니다.

  • 불규칙 사변형 (영국 영어) 또는 부등변 사변형 (trapezium) (북미 영어): 변이 평행하지 않습니다. (영국 영어에서, 이것은 trapezoid라고 불립니다.)
  • 사다리꼴(Trapezium) (UK) 또는 (trapezoid) (US): 적어도 한 쌍의 반대쪽 변은 평행(parallel)입니다. Trapezia (영국) 및 trapezoids (US)는 평행-사변형을 포함합니다.
  • 이등변 사다리꼴(Isosceles trapezium) (UK) 또는 (isosceles trapezoid) (US) : 한 쌍의 반대쪽 변이 평행하고 밑변 각도는 측정에서 같습니다. 대안적인 정의는 한 쌍의 반대쪽 변을 이등분하는 대칭의 축을 가진 사변형 또는 같은 같은 길이의 대각선을 가진 사다리꼴입니다.
  • 평행-사변형(Parallelogram): 두 쌍의 평행한 변을 가진 사변형. 동등한 조건은 반대쪽 변의 길이가 같다는 것입니다; 반대 각도는 같다는 것입니다; 또는 대각선이 서로 이등분한다는 것입니다. 평행-사변형은 rhombi (우리가 정사각형이라고 부르는 사변형을 포함)과 rhomboid (직사각형이라고 부르는 사변형을 포함)을 포함합니다. 다시 말해, 평행 사변형은 모든 마름모(rhombi) 및 모든 럼보이드를 포함하고, 따라서 역시 모든 직사각형을 포함합니다.
  • 마름모(rhombus 또는 rhomb): 모든 네 변이 같은 길이를 가집니다. 동등한 조건은 대각선이 서로를 수직 이등분한다는 것입니다. 비공식적으로: "밀어-넣은 정사각형" (그러나 엄격하게 정사각형을 역시 포함합니다).
  • 럼보이드(Rhomboid): 인접한 변의 비-같은 길이이고 일부 각도가 경사진(oblique) (동등하게, 직각을 가지지 않음) 평행-사변형입니다. 비공식적으로 : "밀어-넣은 직사각형". 모든 참조가 동의하지는 않으며, 일부는 마름모가 아닌 평행-사변형으로 럼보이드를 정의합니다.
  • 직사각형(Rectangle): 모든 네 각도가 직각입니다. 동등한 조건은 대각선이 서로 이등분하고 길이에서 같다는 것입니다. 직사각형은 사각형과 오블롱(oblong)을 포함합니다. 비공식적으로 : "상자 또는 오블롱" (정사각형을 포함합니다).
  • 정사각형(Square) (정규 사변형): 모든 네 변이 같은 길이의 것이고 (등변), 모든 네 각도가 직각입니다. 동등한 조건은 반대쪽 변이 평행 (정사각형은 평행사변형입니다), 대각선이 서로 수직적으로 이등분하고, 같은 길이의 것입니다. 사변형이 정사각형인 것과 그것이 마름모와 직사각형 둘 다 (네 같은 변과 네 같은 길이)인 것은 필요충분 조건입니다.
  • 오블롱(Oblong): 이 용어는 때때로 인접한 변이 서로 다른 직사각형 (즉, 정사각형이 아닌 직사각형)을 나타내기 위해 사용됩니다.
  • 연(Kite): 인접한 두 쌍의 변이 같은 길이의 것입니다. 이것은 하나의 대각선이 연을 합동 삼각형(congruent triangles)으로 나누므로, 따라서 두 쌍의 같은 변 사이의 각도가 측정에서 같음을 의미합니다. 역시 대각선이 수직임을 의미합니다. 연은 마름모를 포함합니다.
  • 접하는 사변형(Tangential quadrilateral): 네 변은 내접된 원에 접합니다. 볼록 사변형이 접하는 것과 반대편 변이 같은 합을 가지는 것은 필요충분 조건입니다.
  • 접하는 사다리꼴(Tangential trapezoid): 네 변이 내접된 원(inscribed circle)에 접하는(tangent) 사다리꼴.
  • 순환 사변형(Cyclic quadrilateral): 네 꼭짓점이 둘레-접하는 원(circumscribed circle) 위에 놓입니다. 볼록 사변형이 순환인 것과 반대편 각도는 합해서 180°가 됩니다.
  • 직각 연(Right kite): 두 반대편 직각을 갖는 연. 순환 사변형의 한 종류입니다.
  • 조화 사변형(Harmonic quadrilateral): 서로 반대의 변의 길이의 곱이 같은 것입니다. 순환 사변형의 한 종류입니다.
  • 이-중심 사변형(Bicentric quadrilateral): 접하는 및 순환 둘 다입니다.
  • 직교-대각 사변형(Orthodiagonal quadrilateral): 대각선이 직각(right angle)에서 교차합니다.
  • 같은-대각선 사변형(Equidiagonal quadrilateral): 대각선이 같은 길이의 것입니다.
  • 외-접하는 사변형(Ex-tangential quadrilateral): 변의 네 확장이 외-원(excircle)에 접하는 것입니다.
  • 어퀼릭 사변형(equilic quadrilateral)은, 확장될 때, 60°에서 만나는 두 반대편 같은 변을 가집니다.
  • 와트 사변형(Watt quadrilateral)은 같은 길이의 한 쌍의 반대편 변을 갖는 사변형입니다.
  • 이차-초곡면 사변형(quadric quadrilateral)은 네 꼭짓점 모두가 정사각형의 둘에 위에 놓이는 볼록 사변형입니다.
  • 지름의 사변형(diametric quadrilateral)은 변의 하나를 둘레-원의 지름으로 갖는 순환 사변형입니다.
  • 헬름슬레브(Hjelmslev quadrilateral)는 반대편 꼭짓점에서 두 직각을 갖는 사변형입니다.

Concave quadrilaterals

오목(concave) 사변형에서, 하나의 내부 각도는 180°보다 크고 두 대각선 중 하나는 사변형 외부에 놓입니다.

  • 다트(dart) (또는 화살-머리)는 연처럼 양쪽 대칭을 갖는 오목 사변형이지만, 하나의 내부 각도는 반사됩니다. (오목) 연을 참조하십시오.

Complex quadrilaterals

자기-교차하는(self-intersecting) 사변형은 다양하게 교차-사변형(cross-quadrilateral), 교차된 사변형(crossed quadrilateral), 나비 사변형(butterfly quadrilateral) 또는 활-매듭 사변형(bow-tie quadrilateral)으로 불립니다. 교차된 사변형에서, 교차하는 양쪽 변에 있는 네 "내부" 각도 (그림이 추적될 때 왼쪽에 모두 또는 오른쪽에 모두, 두 예각(acute)과 두 반사각(reflex))는 합해져서 720°가 됩니다.

Special line segments

볼록 사변형의 두 대각선(diagonal)은 반대쪽 꼭짓점을 연결하는 선분(line segment)입니다.

볼록 사변형의 두 쌍-중앙선(bimedians)은 반대쪽 변의 중간-점을 연결하는 선분입니다. 그것들은 사변형의 "꼭짓점 도형-중심"에서 교차합니다 (아래의 주목할 점(Remarkable points)을 참조하십시오).

볼록 사변형의 네 말티튜드(maltitudes)는 반대쪽 변의 중간-점을 통해 한 변에 수직입니다.

Area of a convex quadrilateral

변 a = AB, b = BC, c = CD and d = DA를 갖는 볼록 사변형 ABCD의 넓이(area) K에 대해 다양한 일반적인 공식이 있습니다.

Trigonometric formulas

그 넓이는 다음으로 삼각법 항에서 표현될 수 있습니다:

\(\quad\displaystyle K = \tfrac{1}{2} pq \cdot \sin \theta,\)

여기서 대각선의 길이는 p와 q이고 그들 사이의 각도는 θ입니다. 직교-대각 사변형의 경우 (예를 들어, 마름모, 정사각형, 및 연)에서, 이 공식은 \(\displaystyle K=\tfrac{1}{2}pq\)로 줄어드는데 왜냐하면 θ가 90°이기 때문입니다.

그 넓이는 다음으로 쌍-중앙선의 관점에서 역시 표현될 수 있습니다:

\(\quad\displaystyle K = mn \cdot \sin \varphi,\)

여기서 쌍-중앙선의 길이는 m과 n이고 그들 사이의 각도는 φ입니다.

브레치나이더 공식(Bretschneider's formula)은 변과 두 반대쪽 각도의 관점에서 넓이를 표현합니다:

\(\quad\displaystyle \begin{align}
K &= \sqrt{(s-a)(s-b)(s-c)(s-d) - \tfrac{1}{2} abcd \; [ 1 + \cos (A + C) ]} \\
&= \sqrt{(s-a)(s-b)(s-c)(s-d) - abcd \left[ \cos^2 \left( \tfrac{A + C}{2} \right) \right]}
\end{align}\)

여기서 수열에서 변은 a, b, c, d, s는 반-둘레이고, A와 C가 두 (사실, 임의의 두) 반대쪽 각도입니다. 이것은 A + C = 180°일 때 순환 사변형의 넓이에 대해 브라마굽타의 공식(Brahmagupta's formula)으로 줄어듭니다.

변 b와 c 사이의 각도 C, 및 변 a와 d 사이의 각도 A를 갖는 변과 각도의 관점에서 또 다른 넓이 공식은 다음입니다:

\(\quad\displaystyle K = \tfrac{1}{2}ad \cdot \sin{A} + \tfrac{1}{2}bc \cdot \sin{C}.\)

순환 사변형의 경우에서, 후자 공식은 \(\displaystyle K = \tfrac{1}{2}(ad+bc)\sin{A}\)이 됩니다.

평행-사변형에서, 반대쪽 변과 각도의 두 쌍이 같은 곳에서, 이 공식은 \(\displaystyle K=ab \cdot \sin{A}\)으로 줄어듭니다.

대안적으로, 우리는 변과 대각선의 교차하는 각도 θ의 관점에서, 이 각도가 90°가 아닌 한, 넓이를 쓸 수 있습니다.

\(\quad\displaystyle K = \frac{|\tan \theta|}{4} \cdot \left| a^2 + c^2 - b^2 - d^2 \right|.\)

평행-사변형의 경우에서, 후자 공식은 \(\displaystyle K = \tfrac{1}{2}|\tan \theta|\cdot \left| a^2 - b^2 \right|\)가 됩니다.

변 a, b, c, d를 포함하는 또 다른 넓이 공식은 다음입니다:

\(\quad\displaystyle K=\tfrac{1}{4}\sqrt{(2(a^2+c^2)-4x^2)(2(b^2+d^2)-4x^2)}\sin{\varphi}\)

여기서 x는 대각선의 중간-점 사이의 거리이고 φ는 쌍-중앙선(bimedian) 사이의 각도입니다.

변 a, b, c, d 및 a와 b 사이의 각도 α를 포함하는 마지막 삼각법 넓이 공식은 다음입니다:

\(\quad\displaystyle K=\tfrac{1}{2}ab\cdot\sin{\alpha}+\tfrac{1}{4}\sqrt{4c^2d^2-(c^2+d^2-a^2-b^2+2ab\cdot\cos{\alpha})^2} ,\)

이것은 단지 첫 번째 부호 +를 −로 바꾸어서 (각도 α의 반대편 볼록 부분을 가지는) 볼록 사변형의 넓이에 대해 역시 사용될 수 있습니다.

Non-trigonometric formulas

다음의 두 공식은 변 a, b, c, d, 반-둘레(semiperimeter) s, 및 대각선 p, q의 관점에서 넓이를 표현합니다:

\(\quad\displaystyle K = \sqrt{(s-a)(s-b)(s-c)(s-d) - \tfrac{1}{4}(ac+bd+pq)(ac+bd-pq)},\)

\(\quad\displaystyle K = \tfrac{1}{4} \sqrt{4p^{2}q^{2}- \left( a^{2}+c^{2}-b^{2}-d^{2} \right) ^{2}}.\)

첫 번째는 순환 사변형 경우에서 브라마굽타의 공식으로 줄어드는데, 왜냐하면 그때에는 pq = ac + bd이기 때문입니다.

넓이는 쌍-중앙선 m, n 및 대각선 p, q의 관점에서 역시 표현될 수 있습니다:

\(\quad\displaystyle K=\tfrac{1}{2}\sqrt{(m+n+p)(m+n-p)(m+n+q)(m+n-q)},\)

\(\quad\displaystyle K=\tfrac{1}{2}\sqrt{p^2q^2-(m^2-n^2)^2}.\)

사실, 네 값 m, n, p, 및 q의 임의의 셋은 넓이의 결정에 대해 충분한데, 왜냐하면 임의의 사변형에서 네 값은 \(\displaystyle p^2+q^2=2(m^2+n^2)\)에 의해 관련되기 때문입니다.

만약 두 쌍-중앙선과 한 대각선의 길이가 주어지면,

\(\quad\displaystyle K=\tfrac{1}{2}\sqrt{[(m+n)^2-p^2]\cdot[p^2-(m-n)^2]},\) 

그리고, 만약 두 대각선과 한 쌍-중앙선의 길이가 주어지면,

\(\quad\displaystyle K=\tfrac{1}{4}\sqrt{[(p+q)^2-4m^2]\cdot[4m^2-(p-q)^2]}\) .

Vector formulas

사변형 ABCD의 넓이는 벡터(vectors)를 사용하여 계산될 수 있습니다. 벡터 AC와 BD가 A에서 C까지 및 B에서 D까지 대각선을 형성한다고 놓습니다. 사변형의 면적은 그런-다음 다음입니다:

\(\quad\displaystyle K = \tfrac{1}{2} |\mathbf{AC}\times\mathbf{BD}|,\)

이것은 벡터 AC와 BD의 교차 곱(cross product)의 크기의 절반입니다. 이-차원 유클리드 공간에서, 벡터 AC를 \((\mathbf{x}_1, \mathbf{y}_1)\)와 같은 데카르트 공간에서 자유 벡터(free vector in Cartesian space)로 및 BD를 \((\mathbf{x}_2, \mathbf{y}_2)\)로 표현하면, 이것은 다음으로 다시-쓸 수 있습니다:

\(\quad\displaystyle K = \tfrac{1}{2} |x_1 y_2 - x_2 y_1|.\)

Diagonals

Properties of the diagonals in some quadrilaterals

다음 테이블에서, 만약 대각선이 가장 기본 사변형 중 일부에서 서로 이등분하면, 만약 대각선이 수직이면, 및 만약 그들의 대각선이 같은 길이를 가지면, 목록화됩니다. 목록은 가장 일반적인 경우에 적용되고, 이름-지은 부분-집합을 제외합니다.

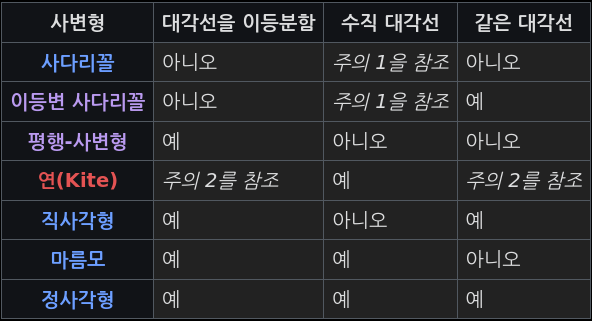
주의 1: 가장 일반적인 사다리꼴 및 이등변 사다리꼴은 수직 대각선을 갖지 않지만, 수직 대각선을 가지고 다른 이름-지정된 사변형이 아닌 (비-유사한) 사다리꼴 및 이등변 사다리꼴의 무한한 숫자가 있습니다.

주의 2: 연에서, 한 대각선이 다른 대각선을 이등분합니다. 가장 일반적인 연은 비-같은 대각선을 가지지만, 대각선이 길이에서 같은 (비-유사한) 연의 무한한 숫자가 있습니다 (그리고 연은 임의의 다른 이름-지은 사변형이 아닙니다).

Lengths of the diagonals

볼록 사변형 ABCD에서 대각선의 길이는 사변형의 하나의 대각선과 두 변에 의해 형성된 각 삼각형에 대한 코사인 법칙(law of cosines)을 사용하여 계산될 수 있습니다. 따라서

\(\quad\displaystyle p=\sqrt{a^2+b^2-2ab\cos{B}}=\sqrt{c^2+d^2-2cd\cos{D}}\)

및

\(\quad\displaystyle q=\sqrt{a^2+d^2-2ad\cos{A}}=\sqrt{b^2+c^2-2bc\cos{C}}.\)

다른, 대각선의 길이에 대해 보다 대칭적 공식은 다음입니다:

\(\quad\displaystyle p=\sqrt{\frac{(ac+bd)(ad+bc)-2abcd(\cos{B}+\cos{D})}{ab+cd}}\)

및

\(\quad\displaystyle q=\sqrt{\frac{(ab+cd)(ac+bd)-2abcd(\cos{A}+\cos{C})}{ad+bc}}.\)

Generalizations of the parallelogram law and Ptolemy's theorem

임의의 볼록한 사변형 ABCD에서, 네 변의 제곱의 합은 두 대각선의 제곱 곱하기 대각선의 중간-점을 연결하는 선분의 제곱의 네 배를 합한 것과 같습니다. 따라서

\(\quad\displaystyle  a^2 + b^2 + c^2 + d^2 = p^2 + q^2 + 4x^2 \)

여기서 x는 대각선의 중간-점 사이의 거리입니다.  이것은 때때로 오일러의 사변형 정리(Euler's quadrilateral theorem)로 알려져 있고 평행-사변형 법칙(parallelogram law)의 일반화입니다.

독일 수학자 카를 안톤 브레치나이더(Carl Anton Bretschneider)는 볼록 사변형에서 대각선의 곱과 관련하여, 프톨레마이오스의 정리(Ptolemy's theorem)의 다음 일반화를 1842년에 유도했습니다:

\(\quad\displaystyle  p^2q^2=a^2c^2+b^2d^2-2abcd\cos{(A+C)}.\)

이 관계는 사변형에 대해 코사인의 법칙(law of cosines)으로 여길 수 있습니다. 순환 사변형(cyclic quadrilateral)에서, 여기서 A + C = 180°이며, 그것은 pq = ac + bd로 줄어듭니다. cos (A + C) ≥ −1이므로, 그것은 역시 프톨레마이오스의 부등식의 증명을 제공합니다.

Other metric relations

만약 X와 Y가 변 a = AB, b = BC, c = CD, d = DA를 갖는 볼록 사변형 ABCD에서 B와 D에서 대각선 AC = p로의 수선의 발이면, 다음입니다:

\(\quad\displaystyle XY=\frac{|a^2+c^2-b^2-d^2|}{2p}.\)

변 a = AB, b = BC, c = CD, d = DA를 갖는 볼록 사변형 ABCD에서, 그리고 여기서 대각선이 E에서 교차하며,

\(\quad\displaystyle  efgh(a+c+b+d)(a+c-b-d) = (agh+cef+beh+dfg)(agh+cef-beh-dfg)\)

여기서 e = AE, f = BE, g = CE, 및 h = DE입니다.

볼록 사변형의 모양과 크기는 수열에서 그것의 변과 두 지정된 꼭짓점 사이의 한 대각선의 길이에 의해 완전히 결정됩니다. 사변형의 두 대각선 p, q 및 네 변 길이 a, b, c, d는 다음과 같이 케일리-멩거(Cayley-Menger) 행렬식(determinant)에 의해, 다음과 같이, 관련됩니다:

\(\quad\displaystyle  \det \begin{bmatrix} 
   0 & a^2 & p^2 & d^2 & 1 \\
 a^2 &   0 & b^2 & q^2 & 1 \\
 p^2 & b^2 &   0 & c^2 & 1 \\
 d^2 & q^2 & c^2 &   0 & 1 \\
   1 &   1 &   1 & 1   & 0
\end{bmatrix} = 0. \)

Angle bisectors

볼록 사변형의 내부 각도 이등분선(angle bisector)은 순환 사변형(cyclic quadrilateral)  (즉, 인접한 각도 이등분선의 네 교차 점은 일치-순환(concyclic)입니다)을 형성하거나 그들은 공점(concurrent)입니다. 후자의 경우에서, 사변형은 접선 사변형(tangential quadrilateral)입니다.

사변형 ABCD에서, 만약 A와 C의 각도 이등분선(angle bisectors)이 대각선 BD 위에서 만나면, B와 D의 각도 이등분선은 대각선 AC 위에서 만납니다.

Bimedians

사변형의 쌍-중앙선(bimedian)은 반대쪽 변의 중간-점(midpoint)을 연결하는 선분입니다. 쌍-중앙선의 교차는 사변형의 꼭짓점의 도형-중심(centroid)입니다.

임의의 사변형 (볼록, 오목 또는 교차된)의 변의 중간-점은 바리논의 평행-사변형(Varignon parallelogram)으로 불리는 평행-사변형(parallelogram)의 꼭짓점입니다. 그것은 다음 속성을 가집니다:

  • 바리논의 평행-사변형의 반대쪽 변의 각 쌍은 원래 사변형에서 대각선에 평행합니다.
  • 바리논의 평행-사변형의 한 변은 그것이 평행한 원래 사변형에서 대각선 길이의 절반입니다.
  • 바리논의 평행-사변형의 넓이는 원래 사변형의 넓이의 절반과 같습니다. 이것은 후자의 넓이가 그것이 구성되는 두 삼각형의 넓이의 차이로 정의되는 것으로 조건으로 하여 볼록, 오목 및 교차된 사변형에서 참입니다.
  • 바리논의 평행-사변형의 둘레(perimeter)는 원래 사변형의 대각선의 합과 같습니다.
  • 바리논의 평행-사변형의 대각선은 원래 사변형의 쌍-중앙선입니다.

사변형에서 두 쌍-중앙선과 해당 사변형에서 대각선의 중간-점을 연결하는 선분은 공점(concurrent)이고 교차의 그들의 점에 의해 모두 이등분됩니다.

변 a, b, c 및 d를 갖는 볼록 사변형에서, 변 a와 c의 중간-점을 연결하는 쌍-중앙선의 길이는 다음입니다:

\(\quad\displaystyle m=\tfrac{1}{2}\sqrt{-a^2+b^2-c^2+d^2+p^2+q^2}\)

여기서 p와 q는 대각선의 길이입니다. 변 b와 d의 중간-점을 연결하는 쌍-중앙선의 길이는 다음입니다:

\(\quad\displaystyle n=\tfrac{1}{2}\sqrt{a^2-b^2+c^2-d^2+p^2+q^2}.\)

따라서

\(\quad\displaystyle \displaystyle p^2+q^2=2(m^2+n^2).\)

이것은 바리논의 평행-사변형에 적용된 평행-사변형 법칙(parallelogram law)에 대한 역시 따름정리(corollary)입니다.

쌍-중앙선의 길이는 두 반대쪽 변과 대각선의 중간-점 사이의 거리 x의 관점에서 역시 표현될 수 있습니다. 이것은 위의 공식에서 오일러의 사변형 정리를 사용할 때 가능합니다. 출처로부터

\(\quad\displaystyle m=\tfrac{1}{2}\sqrt{2(b^2+d^2)-4x^2}\)

및

\(\quad\displaystyle n=\tfrac{1}{2}\sqrt{2(a^2+c^2)-4x^2}.\)

이들 공식에서 두 반대쪽 변은 쌍-중앙선이 연결하는 둘이 아닌 것임에 주목하십시오.

볼록 사변형에서, 쌍-중앙선과 대각선 사이에 다음 이중(dual) 연결이 있습니다:

  • 두 쌍-중앙선이 같은 길이를 갖는 것과 두 대각선이 수직(perpendicular)인 것은 필요충분(iff) 조건입니다.
  • 두 쌍-중앙선이 수직인 것과 두 대각선이 같은 길이를 갖는 것은 필요충분 조건입니다.

Trigonometric identities

단순 사변형 ABCD의 네 각도는 다음 항등식을 만족시킵니다:

\(\quad\displaystyle \sin{A}+\sin{B}+\sin{C}+\sin{D}=4\sin{\frac{A+B}{2}}\sin{\frac{A+C}{2}}\sin{\frac{A+D}{2}}\)

및

\(\quad\displaystyle \frac{\tan{A}\tan{B}-\tan{C}\tan{D}}{\tan{A}\tan{C}-\tan{B}\tan{D}}=\frac{\tan{(A+C)}}{\tan{(A+B)}}.\)

역시,

\(\quad\displaystyle \frac{\tan{A}+\tan{B}+\tan{C}+\tan{D}}{\cot{A}+\cot{B}+\cot{C}+\cot{D}}=\tan{A}\tan{B}\tan{C}\tan{D}.\)

마지막 두 공식에서, 각도는 직각(right angle)이 되는 것이 허용되지 않는데, 왜냐하면 tan 90°가 정의되지 않기 때문입니다.

Inequalities

Area

만약 볼록 사변형이 연속 변 a, b, c, d와 대각선 p, q를 가지면, 그것의 넓이 K는 다음을 만족시킵니다:

  • 직사각형(rectangle)에 대해 오직 상등을 갖는 \(\displaystyle K\le \tfrac{1}{4}(a+c)(b+d)\).
  • 정사각형(square)에 대해 오직 상등을 갖는 \(\displaystyle K\le \tfrac{1}{4}(a^2+b^2+c^2+d^2)\).
  • 만약 대각선이 수직이고 같으면 오직 상등을 갖는 \(\displaystyle K\le \tfrac{1}{4}(p^2+q^2)\).
  • 직사각형에 대해 오직 상등을 갖는 \(\displaystyle K\le \tfrac{1}{2}\sqrt{(a^2+c^2)(b^2+d^2)}\).

브레치나이더 공식(Bretschneider's formula)으로부터, 사변형의 넓이는 다음을 만족시킴을 직접 따릅니다:

\(\quad\displaystyle K \le \sqrt{(s-a)(s-b)(s-c)(s-d)}\)

상등을 갖는 것과 사변형이 순환(cyclic) 또는 한 변이 다른 셋의 합과 같은 것을 만족하는 퇴화 (그것은 선분(line segment)으로 접히므로, 넓이는 영입니다)인 것은 필요충분(iff) 조건입니다.

임의의 사변형의 넓이는 다음 부등식을 만족시킵니다:

\(\quad\displaystyle \displaystyle K\le \tfrac{1}{2}\sqrt[3]{(ab+cd)(ac+bd)(ad+bc)}.\)

둘레를 L로 표시하면, 우리는 다음을 가집니다:

\(\quad\displaystyle K\le \tfrac{1}{16}L^2,\)

상등은 정사각형의 경우에서 오직 가집니다.

볼록 사변형의 넓이는 역시 다음을 만족시킵니다:

\(\quad\displaystyle K \le \tfrac{1}{2}pq\)

대각 길이 p와 q에 대해, 상등을 갖는 것과 대각선이 수직인 것은 필요충분 조건입니다.

a, b, c, d를 넓이 K와 대각선 AC = p, BD = q을 갖는 볼록 사변형 ABCD의 변의 길이로 놓습니다. 그런-다음

\(\quad\displaystyle  K \leq \frac{a^2+b^2+c^2+d^2+p^2+q^2+pq-ac-bd}{8} \) with equality only for a square.

a, b, c, d를 넓이 K를 갖는 볼록 사변형 ABCD의 변의 길이로 놓습니다. 그런-다음 다음 부등식이 만족됩니다:

\(\quad\displaystyle  K \leq \frac{1}{3+\sqrt{3}}(ab+ac+ad+bc+bd+cd)- \frac{1}{2(1+\sqrt{3})^2}(a^2+b^2+c^2+d^2) \) 정사각형에 대해 오직 상등을 가집니다.

Diagonals and bimedians

오일러의 사변형 정리에 대한 따름정리는 다음 부등식입니다:

\(\quad\displaystyle  a^2 + b^2 + c^2 + d^2 \ge p^2 + q^2 \)

여기서 상등이 유지되는 것과 사변형이 평행-사변형(parallelogram)인 것은 필요충분 조건입니다.

오일러(Euler)는 역시 프톨레마이오스의 정리(Ptolemy's theorem)를 볼록 사변형에 대해 부등식으로 일반화했으며, 그 정리는 순환 사변형(cyclic quadrilateral)에서 상등입니다. 그것은 다음임을 말합니다:

\(\quad\displaystyle  pq \le ac + bd \)

여기서 상등인 것과 사변형이 순환인 것은 필요충분(iff) 조건입니다.  이것은 종종 프톨레마이오스의 정리(Ptolemy's theorem)라고 불립니다.

임의의 볼록 사변형에서, 쌍-중앙선 m, n과 대각선 p, q는 다음 부등식에 의해 관련됩니다:

\(\quad\displaystyle pq \leq m^2+n^2,\)

상등이 유지되는 것과 대각선이 같은 것은 필요충분 조건입니다. 이것은 사변형 항등식 \(\displaystyle m^2+n^2=\tfrac{1}{2}(p^2+q^2)\)으로부터 직접 따릅니다.

Sides

임의의 사변형의 변 a, b, c, 및 d는 다음을 만족시킵니다:

\(\quad\displaystyle a^2+b^2+c^2 > \frac{d^2}{3}\)

및

\(\quad\displaystyle a^4+b^4+c^4 \geq \frac{d^4}{27}.\)

Maximum and minimum properties

주어진 둘레(perimeter)를 가진 모든 사변형 중의, 가장 큰 넓이를 가진 것은 정사각형(square)입니다. 이것은 사변형에 대해 같은-둘레 정리(isoperimetric theorem)라고 불립니다. 그것은 넓이 부등식의 직접적인 결과입니다:

\(\quad\displaystyle K\le \tfrac{1}{16}L^2\)

여기서 K는 둘레 L을 가진 볼록 사변형의 넓이입니다. 상등이 유지되는 것과 사변형이 정사각형인 것은 필요충분(iff) 조건입니다. 이중 정리는 주어진 넓이를 갖는 모든 사각형에 대해, 정사각형이 가장-짧은 둘레를 가진다고 말합니다.

최대(maximum) 넓이를 가지는 주어진 변 길이를 갖는 사변형은 순환 사변형(cyclic quadrilateral)입니다.

주어진 대각선을 갖는 모든 볼록 사변형의, 직교-대각 사변형(orthodiagonal quadrilateral)은 가장-큰 넓이를 가집니다.  이것은 볼록 사변형의 넓이가 다음을 만족시킨다는 사실의 직접 결과입니다:

\(\quad\displaystyle K=\tfrac{1}{2}pq\sin{\theta}\le \tfrac{1}{2}pq,\)

여기서 θ는 대각선 p와 q 사이의 각도입니다. 상등이 유지되는 것과 θ = 90°인 것은 필요충분 조건입니다.

만약 P가 볼록 사변형 ABCD에서 내부 점이면, 다음입니다:

\(\quad\displaystyle AP+BP+CP+DP\ge AC+BD.\)

이 부등식으로부터, 꼭짓점(vertices)에 대한 거리의 합을 최소화(minimizes)하는 사변형 내부의 점은 대각선의 교차임을 따릅니다. 따라서 해당 점은 볼록 사변형의 페르마 점(Fermat point)입니다.

Remarkable points and lines in a convex quadrilateral

사변형의 중심은 여러 다른 방식으로 정의될 수 있습니다. "꼭짓점 도형-중심"은 사변형이 비어 있지만 꼭짓점에 같은 질량을 갖는 것으로 여기는 것으로부터 옵니다. "변 도형-중심"은 변을 단위 길이 당 상수 질량을 가지는 것으로 고려함으로부터 나옵니다. 단지 도형-중심(centroid) (넓이의 중심)이라고 불리는 보통의 중심은 상수 밀도를 가지는 사변형의 표면을 고려함으로부터 나옵니다. 이들 세 점이 일반적으로 모두 같은 점은 아닙니다.

"꼭짓점 도형-중심"은 두 쌍-중앙선(bimedians)의 교차입니다. 임의의 다각형과 마찬가지로, 꼭짓점 도형-중심의 x와 y 좌표는 꼭짓점의 x와 y 좌표의 산술 평균(arithmetic mean)입니다.

사변형 ABCD의 "넓이 도형-중심"은 다음 방법으로 구성될 수 있습니다. \(G_a, G_b, G_c, G_d\)를 각각 삼각형 BCD, ACD, ABD, ABC의 도형-중심으로 놓습니다. 그런-다음 "넓이 도형-중심"은 직선 \(G_a G_c\)와 \(G_b G_d\)의 교차입니다.

일반적인 볼록 사변형 ABCD에서, 삼각형(triangle)의 둘레-중심(circumcenter)과 수직-중심(orthocenter)에 대한 자연스러운 유사성은 없습니다. 그러나 두 그러한 점은 다음 방식에서 구성될 수 있습니다. \(O_a, O_b, O_c, O_d\)를 각각 삼각형 BCD, ACD, ABD, ABC의 둘레-중심이라고 놓습니다; 그리고 같은 삼각형에서 수직-중심을 \(H_a, H_b, H_c, H_d\)에 의해 나타냅니다. 그런-다음 직선 \(O_a O_c\)와 \(O_b O_d\)의 교차는 준-둘레-중심(quasicircumcenter)이라고 불리고 직선 \(H_a H_c\)와 \(H_b H_d\)의 교차는 볼록 사변형의 준-수직-중심(quasiorthocenter)이라고 불립니다. 이들 점은 사변형의 오일러 직선(Euler line)을 정의하기 위해 사용될 수 있습니다. 볼록 사변형에서, 준-수직-중심 H, "넓이 도형-중심" G, 및 준-둘레-중심 O는 이 순서대로 같은-직선(collinear)이고, HG = 2GO입니다.

직선 \(E_a E_c\)와 \(E_b E_d\)의 교차로 준-아홉-점 중심 E를 역시 정의할 수 있으며, 여기서 \(E_a, E_b, E_c, E_d\)는 각각 삼각형 BCD, ACD, ABD, ABC의 아홉-점 중심(nine-point centers)입니다. 그런-다음 E는 OH의 중간-점(midpoint)입니다.

볼록한 비-평행사변형 사변형의 또 다른 주목할만한 직선은 대각선의 중간-점을 연결하는 뉴턴 직선(Newton line)이며, 이들 점들을 연결하는 선분은 꼭짓점 도형-중심에 의해 이등분됩니다. 한 가지 더 흥미로운 직선 (어떤 의미에서 뉴턴의 직선과 이중)은 대각선의 교차의 점을 꼭짓점 도형-중심과 연결하는 직선입니다. 그 직선은 (넓이) 도형-중심을 포함한다는 사실에 주목할만합니다. 꼭짓점 도형-중심은 대각선의 교차와 (넓이) 도형-중심을 연결하는 선분을 3:1의 비율로 나눕니다.

각각, AD와 BC 및 AB와 CD의 교차 점 P와 Q를 갖는 임의의 사변형 ABCD에 대해, 원 (PAB), (PCD), (QAD), 및 (QBC)는 미켈 점(Miquel point)으로 불리는 공통 점 M을 통과합니다.

볼록 사변형 ABCD에 대해, E는 대각선의 교차의 점이고 F는 변 BC와 AD의 연장선의 교차의 점이며, ω를 M에서 내부적으로 CB와 만나고 N에서 내부적으로 DA에서 만나는 E와 F를 통과하는 원으로 놓습니다. CA가 L에서 다시 ω와 만나는 것으로 놓고 DB를 K에서 다시 ω에서 만나는 것으로 놓습니다. 그런-다음 다음이 유지됩니다: 직선 NK와 ML은 변 AB 위에 위치되는 점 P에서 교차합니다; 직선 NL과 KM은 변 CD 위에 위치되는 점 Q에서 교차합니다. 점 P와 Q는 변 AB와 CD 위에 원 ω에 의해 형성된 "파스칼 점"이라고 불립니다.

Other properties of convex quadrilaterals

  • 외부 정사각형을 사변형의 모든 변 위에 그려지도록 놓습니다. 반대편 정사각형의 중심(centers)을 연결하는 선분은 (a) 길이에서 같고 (b) 수직(perpendicular)입니다. 따라서, 이들 중심은 직교-대각 사변형(orthodiagonal quadrilateral)의 꼭짓점입니다. 이것은 폰 오우벨의 정리(Van Aubel's theorem)라고 불립니다.
  • 주어진 가장자리 길이를 가진 임의의 단순 사변형에 대해, 같은 가장자리 길이를 가진 순환 사변형이 있습니다.
  • 네 작은 삼각형은 두 반대편 삼각형의 넓이의 곱이 다른 두 삼각형의 곱과 같은 속성을 가지는 볼록 사변형의 대각선과 변에 의해 형성됩니다.

Taxonomy

사변형의 계층적 분류(taxonomy)는 오른쪽 그림에 나와 있습니다. 더 낮은 계층은 그들이 연결되는 더 높은 계층의 특수한 경우입니다. 여기서 "사다리꼴(trapezoid)"은 북미 정의를 참조함에 주목하십시오 (영국식은 trapezium에 동등합니다). 포괄적인 정의가 전체적으로 사용됩니다.

Skew quadrilaterals

비-평면 사변형은 꼬인 사변형(skew quadrilateral)이라고 불립니다. 가장자리 길이로부터 이면각과 두 인접한 가장자리 사이의 각도를 계산하는 공식은 네 원자의 "주름-잡힌" 링을 포함하는 사이클로뷰테인(cyclobutane)과 같은 분자의 특성에 대한 연구를 위해 도출되었습니다. 역사적으로 용어 고쉬 사변형(gauche quadrilateral)은 꼬인 사변형을 의미하기 위해 역시 사용되었습니다. 그것의 대각선과 함께 꼬인 사변형은 (아마도 비-정규) 사면체(tetrahedron)를 형성하고, 반대로 모든 각 꼬인 사변형은 한 쌍의 반대쪽 가장자리(edge)가 제거된 사면체에서 나옵니다.

External links