영문 위키피디아 번역

(번역) Concave function

다움위키 2024. 1. 18. 17:57
Original article: wikipedia:Concave function

 
수학(mathematics)에서 오목 함수(concave function)는 볼록 함수(convex function)의 부정(negative)입니다. 오목 함수는 아래로 오목(concave downwards), 오목한 아래쪽(concave down), 위로 볼록(convex upwards), 볼록한 모자(convex cap) 또는 볼록한 위쪽(upper convex)으로 역시 동의적으로 불립니다.

Definition

구간(interval) (또는, 보다 일반적으로, 벡터 공간(vector space)에서 볼록 집합(convex set)) 위에 실제-값 함수(function) \(f\)는, 만약 구간에서 임의의 \(x\)와 \(y\)에 대해 임의의 \(\alpha \in [0,1]\), 다음이면, 오목이라고 말합니다:

\(\quad f((1-\alpha )x+\alpha y)\geq (1-\alpha ) f(x)+\alpha f(y)\).

함수가, 만약, 임의의 \(\alpha \in (0,1)\) 및 \(x \neq y\)에 대해 다음이면, 엄격하게 오목이라고 불립니다:

\(\quad f((1-\alpha )x + \alpha y) > (1-\alpha) f(x) + \alpha f(y)\,\).

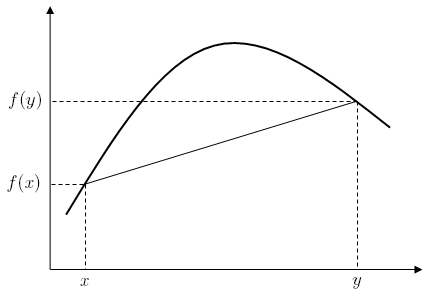
함수 \(f: \mathbb{R} \to \mathbb{R}\)에 대해, 이 두 번째 정의는 단지 \(x\) 및 \(y\) 사이의 엄격하게 모든 각 \(z\)에 대해, \(f\)의 그래프 위의 점 \((z, f(z))\)는 점 \((x, f(x))\)와 \((y, f(y))\)를 연결하는 직선 위쪽에 있음을 말합니다.

함수 \(f\)는, 만약 함수 \(S(a)=\{x: f(x)\geq a\}\)의 위쪽 윤곽 집합이 볼록 집합이면, 유사-오목(quasiconcave)입니다.

Properties

Functions of a single variable

1. 미분-가능한(differentiable) 함수(function) f가 하나의 구간(interval) 위에 (엄격하게) 오목인 것은 그의 도함수(derivative) 함수 f ′이 해당 구간 위에 (엄격하게) 단조롭게 감소하는(monotonically decreasing) 것, 즉, 오목 함수가 비-증가하는 (감소하는) 기울기(slope)를 갖는 것과 필요충분 조건입니다.
2. 오목성이 변하는 (오목과 볼록(convex) 사이의) 점(Points)은 변곡 점(inflection point)입니다.
3. 만약 f가 두번-미분 가능(differentiable)이면, f가 오목인 것과 f ′′가 비-양수(non-positive) (또는, 비공식적으로, 만약 "가속도"가 비-양수)인 것은 필요충분 조건입니다. 만약 그의 이차 도함수가 음수(negative)이면, 그것은 엄격하게 오목이지만, 역은, \(f(x)=-x^4\)에서 보여진 것처럼, 참이 아닙니다.
4. 만약 f가 오목이고 미분-가능이면, 그것은 그의 일-차 테일러 근사(Taylor approximation)에 의해 위로 경계집니다:
\(\quad\displaystyle f\left( \frac{x+y}2 \right) \ge \frac{f(x) + f(y)}2\)

5. 구간 C 위에 르베그 측정-가능 함수(Lebesgue measurable function)가 오목인 것과 그것은 중점 오목, 즉, C에서 임의의 x와 y에 대해 다음인 것은 필요충분(iff) 조건입니다:
\(\quad\displaystyle f\left( \frac{x+y}2 \right) \ge \frac{f(x) + f(y)}2\)
6. 만약 함수 f가 오목이고, f(0) ≥ 0이면, f는 \([0,\infty)\) 위에 부분-덧셈적(subadditive)입니다. 증명:

  • f가 오목이고 1 ≥ t ≥ 0이므로, y = 0를 설정하면, 우리는 \(f(tx) = f(tx+(1-t)\cdot 0) \ge t f(x)+(1-t)f(0) \ge t f(x)\)를 가집니다.
  • \(a,b\in[0,\infty)\)에 대해 다음입니다:

\(\quad\displaystyle f(a) + f(b) = f \left((a+b) \frac{a}{a+b} \right) + f \left((a+b) \frac{b}{a+b} \right) \ge \frac{a}{a+b} f(a+b) + \frac{b}{a+b} f(a+b) = f(a+b)\)

 

Functions of n variables

1. 함수 f가 볼록 집합에 걸쳐 오목인 것과 함수 −f가 그 집합에 걸쳐 볼록 함수(convex function)인 것은 필요충분(iff) 조건입니다.
2. 두 오목 함수의 합은 자체로 오목이고 그래서 두 오목 함수의 점별 최솟값, 즉, 주어진 도메인 위의 오목 함수의 집합은 반-필드(semifield)를 형성합니다.
3. 함수 영역 내부의 지역 최댓값(local maximum) 근처에서, 함수는 반드시 오목해야 합니다; 부분 역으로써, 만약 엄격하게 오목 함수의 도함수가 어떤 점에서 영이면, 해당 점은 지역 최댓값입니다.
4. 오목 함수의 임의의 지역 최댓값(local maximum)은 역시 전역 최댓값(global maximum)입니다. 엄격하게 오목 함수는 많아야 하나의 전역 최댓값을 가질 것입니다.

Examples

  • 함수 \(f(x)=-x^2\) 및 \(g(x)=\sqrt{x}\)는 그들의 도메인 위에 오목인데, 왜냐하면 그들의 이차 도함수 \(f''(x) = -2\) 및 \(\displaystyle g''(x) = -\frac{1}{4 x^{3/2}}\)는 항상 음수이기 때문입니다.
  • 로그(logarithm) 함수 \(f(x) = \log{x}\)는 그의 도메인 \((0,\infty)\) 위에 오목인데, 왜냐하면 그의 도함수 \(\frac{1}{x}\)는 엄격하게 감소하는 함수이기 때문입니다.
  • 임의의 아핀 함수(affine function) \(f(x)=ax+b\)는 오목 및 볼록 둘 다이지만, 엄격하게-오목도 아니고 엄격하게-볼록도 아닙니다.
  • 사인(sine) 함수는 구간 \([0, \pi]\) 위에 오목입니다.
  • 함수 \(f(B) = \log |B|\)는 오목이며, 여기서 \(|B|\)는 비-음의-명확한 행렬(nonnegative-definite matrix) B의 행렬식(determinant)입니다.

Applications

Further References