유클리드 기하학(Euclidean geometry)에서, 직교대각선 사변형은 대각선(diagonal)이 직각(right angle)에서 교차하는 사변형(quadrilateral)입니다. 다시 말해서, 그것은 비-인접한 꼭짓점(vertices) 사이의 선분(line segment)이 서로 직교(orthogonal) (수직)인 넷의-변 도형입니다.
Special cases
연(kite) 하나의 대각선이 대칭의 직선인 직교대각선 사변형입니다. 연은 네 변 모두에 접하는 원(circle)을 포함하는 정확하게 직교대각선 사변형입니다; 즉, 연은 접하는(tangential) 직교대각선 사변형입니다.
마름모(rhombus)는 두 쌍의 평행 변을 갖는 직교대각선 사변형입니다 (즉, 평행사변형(parallelogram)이기도 한 직교대각선 사변형입니다).
정사각형(square)은 연과 마름모 둘 다의 극한하는 경우입니다.
대각선 길이가 적어도 사변형의 모든 변의 길이만큼 긴 직교 같은-대각선(equidiagonal) 사변형은 모든 사변형 중 지름에 대한 최대 넓이를 가지며, 최대 작은 다각형(biggest little polygon) 문제의 n = 4 경우를 해결합니다. 정사각형은 그러한 사변형 중 하나이지만, 무한하게 많은 것들이 있습니다. 역시 등대각선인 직교 사변형은 바리논의 평행-사변형(Varignon parallelogram)이 정사각형이기 때문에 중간-정사각형 사변형(midsquare quadrilateral)입니다. 그 넓이는 순수하게 변의 크기로 표현될 수 있습니다.
Characterizations
임의의 직교대각선 사변형에 대해, 두 반대편 변의 제곱의 합은 다른 두 반대편 변의 제곱의 합과 같습니다: 연속적인 변 a, b, c, 및 d에 대해, 우리는 다음을 가집니다:
\(\quad \displaystyle a^2+c^2=b^2+d^2. \)
이것은 피타고라스 정리(Pythagorean theorem)에서 따른 것인데, 이들 두 제곱의 합 중 하나는 사변형의 꼭짓점에서 대각선이 교차하는 점까지의 넷의 제곱된 거리의 합과 같도록 확장될 수 있습니다. 반대로, \(a^2+c^2=b^2+d^2\)인 임의의 사변형은 직교대각선이어야 합니다. 이것은 코사인 법칙(law of cosines), 벡터(vectors), 간접 증명(indirect proof), 및 복소수(complex number)를 사용하는 것을 포함하여 다양한 방법으로 입증될 수 있습니다.
볼록 사변형의 대각선이 수직인 것과 둘의 쌍-중앙선(bimedians)이 같은 길이를 가지는 것은 필요충분(iff) 조건입니다.
다른 특성화에 따르면, 볼록 사변형 ABCD의 대각선이 수직인 것과 다음인 것은 필요충분 조건입니다:
\(\quad\displaystyle \angle PAB + \angle PBA + \angle PCD + \angle PDC = \pi\)
여기서 P는 대각선의 교차점입니다. 이 방정식으로부터, 거의 즉시 볼록 사변형의 대각선이 수직인 것과 대각 교차점을 사변형의 변 위로의 투영(projections)이 순환 사변형(cyclic quadrilateral)의 꼭짓점인 것이 필요충분 조건이 따릅니다.
볼록 사변형이 직교대각선인 것과 그것의 꼭짓점이 그것의 변의 중간점(midpoint)인 바리논의 평행-사변형(Varignon parallelogram)이 직사각형(rectangle)인 것은 필요충분 조건입니다. 관련된 특성화는 볼록 사변형이 직교대각선인 것과 넷의 적도(maltitudes)의 변과 발의 중간점이 여덟 일치-순환 점(concyclic points): 여덟 점 원(eight point circle)인 것이 필요충분 조건임을 말합니다. 이 원의 중심은 사변형의 도형중심(centroid)입니다. 적도의 발에 의해 형성된 사변형을 주요 직교 사변형(principal orthic quadrilateral)이라고 불립니다.
만약 대각선 교차를 통한 볼록 사변형 ABCD의 변에 대한 법선(normals)이 R, S, T, U에서 반대편 변을 교차하고, K, L, M, N가 이들 법선의 발이면, ABCD가 직교대각선인 것과 여덟 점 K, L, M, N, R, S, T and U이 일치-순환적; 두 번째 여덟 점 원(second eight point circle)인 것은 필요충분 조건입니다. 관련된 특성화는 볼록 사변형이 직교대각선인 것과 RSTU이 그것의 변이 ABCD의 대각선에 평행(parallel)한 직사각형인 것은 필요충분 조건임을 말합니다.
대각선 교차 P와 볼록 사변형 ABCD의 꼭짓점에 의해 형성된 넷의 삼각형(triangle)에 관련하는 몇 가지 메트릭 특성화가 있습니다. \(m_1, m_2, m_3, m_4\)는 삼각형 ABP, BCP, CDP, DAP에서 P에서 변 AB, BC, CD, DA까지의 중앙선(medians)을 각각 나타냅니다. 만약 \(R_1, R_2, R_3, R_4\) 및 \(h_1, h_2, h_3, h_4\)가 이들 삼각형 각각의 둘레원의 반지름과 고도를 나타내면, 사변형 ABCD이 직교대각선인 것과 다음 등식 중 임의의 하나가 유지되는 것은 필요충분 조건입니다:
- \(\displaystyle m_1^2+m_3^2=m_2^2+m_4^2\)
- \(\displaystyle R_1^2+R_3^2=R_2^2+R_4^2\)
- \(\displaystyle \frac{1}{h_1^2}+\frac{1}{h_3^2}=\frac{1}{h_2^2}+\frac{1}{h_4^2}\)
게다가, 대각선의 교차점 P를 갖는 사변형 ABCD가 직교대각선인 것과 삼각형 ABP, BCP, CDP 및 DAP의 둘레중심이 사변형 변의 중간점인 것은 필요충분 조건입니다.
Comparison with a tangential quadrilateral
접하는 사변형(tangential quadrilateral)과 직교대각선 사변형의 몇 가지 메트릭 특성화는 이 테이블에서 볼 수 있듯이, 모양에서 매우 유사합니다. 변 a, b, c, d, 둘레반지름 \(R_1, R_2, R_3, R_4\), 및 고도 \(h_1, h_2, h_3, h_4\)의 표기법은 두 유형의 사변형에서 위와 같습니다.

Area
직교대각선 사변형의 넓이 K는 대각선 p와 q의 길이의 곱의 절반과 같습니다:
\(\quad\displaystyle K=\frac{p\cdot q}{2}.\)
반대로, 넓이가 이 공식으로 계산될 수 있는 임의의 볼록 사변형은 직교대각선이어야 합니다. 직교대각선 사변형은 주어진 대각선을 갖는 모든 볼록 사변형 중 가장 큰 넓이를 가집니다.
Other properties
- 직교대각선 사변형은 대각선에 의해 형성된 변과 각도가 넓이를 고유하게 결정하지 않는 유일한 사변형입니다. 예를 들어, 두 마름모는, 둘 다가 공통 변 a를 갖지만 (및, 모든 마름모에 대한 것처럼, 둘 다는 대각선 사이에 직각을 가짐), 하나는 다른 마름모보다 더 작은 예각(acute angle)을 가지면, 다른 넓이를 가집니다 (전자의 넓이는 예각이 영으로 접근할 때 영으로 접근합니다).
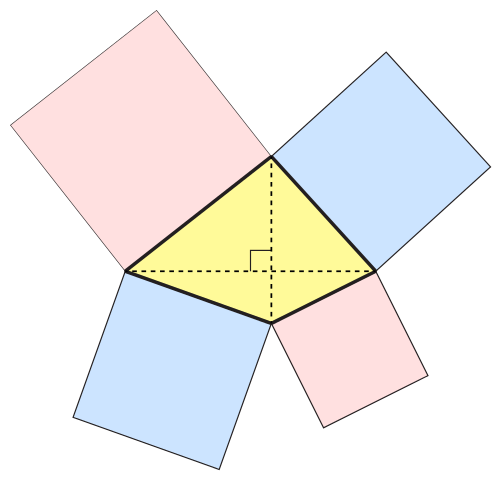
- 만약 정사각형(square)이 임의의 (볼록, 오목, 또는 교차된) 사변형의 변에 바깥쪽으로 세워지면, 그것들의 중심(center) (도형중심(centroid))은 역시 같은-대각선(equidiagonal) (즉, 같은 길이의 대각선을 가짐)인 직교대각선 사변형의 꼭짓점입니다. 이것은 판 오벨의 정리(van Aubel's theorem)라고 불립니다.
- 직교대각선 사변형의 각 변은 파스칼 점 원과 적어도 하나의 공통점을 가집니다.
Properties of orthodiagonal quadrilaterals that are also cyclic
Circumradius and area
순환(cyclic) 직교대각선 사변형 (원(circle)에 내접(inscribed)될 수 있는 것)에 대해, 대각선의 교차점이 한 대각선을 길이 \(p_1\)과 \(p_2\)의 선분으로 나누고 다른 대각선을 길이 \(q_1\)과 \(q_2\)의 선분으로 나눈다고 가정합니다. 그런 다음 (첫 번째 상등은 아르키메데스(Archimedes) 보조정리의 책(Book of Lemmas)의 제안 11입니다)
\(\quad\displaystyle D^2=p_1^2+p_2^2+q_1^2+q_2^2=a^2+c^2=b^2+d^2 \)
여기서 D는 둘레원(circumcircle)의 지름(diameter)입니다. 이것은 대각선이 원의 수직 현이기 때문입니다. 이들 방정식은 다음 둘레반지름(circumradius) 표현을 산출합니다:
\(\quad\displaystyle R=\tfrac{1}{2}\sqrt{p_1^2+p_2^2+q_1^2+q_2^2} \)
또는, 사변형의 변의 관점에서, 다음으로 산출됩니다:
\(\quad\displaystyle R=\tfrac{1}{2}\sqrt{a^2+c^2}=\tfrac{1}{2}\sqrt{b^2+d^2}. \)
역시 다음임을 따릅니다:
\(\quad\displaystyle a^2+b^2+c^2+d^2=8R^2. \)
따라서, 오일러의 사변형 정리(Euler's quadrilateral theorem)에 따르면, 둘레반지름은 대각선 p와 q와 대각선의 중점 사이의 거리 x의 항으로 다음처럼 표현될 수 있습니다:
\(\quad\displaystyle R=\sqrt{\frac{p^2+q^2+4x^2}{8}}. \)
넷의 변의 관점에서 순환 직교대각선 사변형의 넓이(area) K에 대해 공식은 프톨레마이오스의 정리(Ptolemy's theorem)와 직교대각선 사변형의 넓이(area of an orthodiagonal quadrilateral)에 대해 공식을 결합할 때 직접 얻어질 수 있습니다. 그 결과는 다음입니다:
\(\quad\displaystyle K=\tfrac{1}{2}(ac+bd). \)
Other properties
- 순환 직교대각선 사변형에서, 반중심(anticenter)은 대각선이 교차하는 점과 일치합니다.
- 브라마굽타의 정리(Brahmagupta's theorem)는 순환 직교대각선 사변형에 대해, 대각선의 교차점을 통해 임의의 변에서 수직이 반대편 변을 이등분한다고 말합니다.
- 만약 직교대각선 사변형이 역시 순환적이면, 둘레중심(circumcenter) (둘레접된 원의 중심)에서 임의의 변까지의 거리는 반대쪽 변의 길이의 절반과 같습니다.
- 순환 직교대각선 사변형에서, 대각선의 중간점 사이의 거리는 둘레중심과 대각선이 교차하는 점 사이의 거리와 같습니다.
Infinite sets of inscribed rectangles
모든 각 직교대각선 사변형에 대해, 우리는 둘의 무한 직사각형의 집합을 내접할 수 있습니다:
(i) 그것의 한 변이 사변형의 대각선과 평행한 직사각형의 집합
(ii) 파스칼-점 원에 의해 정의된 직사각형의 집합.
References
- Josefsson, Martin (2010), "Calculations concerning the tangent lengths and tangency chords of a tangential quadrilateral" (PDF), Forum Geometricorum, 10: 119–130.
- Altshiller-Court, N. (2007), College Geometry, Dover Publications. Republication of second edition, 1952, Barnes & Noble, pp. 136-138.
- Mitchell, Douglas, W. (2009), "The area of a quadrilateral", The Mathematical Gazette, 93 (July): 306–309.
- Ismailescu, Dan; Vojdany, Adam (2009), "Class preserving dissections of convex quadrilaterals" (PDF), Forum Geometricorum, 9: 195–211.
- Josefsson, Martin (2012), "Characterizations of Orthodiagonal Quadrilaterals" (PDF), Forum Geometricorum, 12: 13–25.
- Mammana, Maria Flavia; Micale, Biagio; Pennisi, Mario (2011), "The Droz-Farny Circles of a Convex Quadrilateral" (PDF), Forum Geometricorum, 11: 109–119.
- Harries, J. (2002), "Area of a quadrilateral", The Mathematical Gazette, 86 (July): 310–311
- David, Fraivert (2017), "Properties of a Pascal points circle in a quadrilateral with perpendicular diagonals" (PDF), Forum Geometricorum, 17: 509–526.
- Posamentier, Alfred S.; Salkind, Charles T. (1996), Challenging Problems in Geometry (second ed.), Dover Publications, pp. 104–105, #4–23.
- Josefsson, Martin (2016), "Properties of Pythagorean quadrilaterals", The Mathematical Gazette, 100 (July): 213–224.
- David, Fraivert (2019), "A Set of Rectangles Inscribed in an Orthodiagonal Quadrilateral and Defined by Pascal-Points Circles", Journal for Geometry and Graphics, 23: 5–27.

