물리학(physics)에서, 일(work)은 변위(displacement)를 따라 힘(force)의 적용을 통해 물체로 또는 물체로부터 전달되는 에너지(energy)입니다. 가장 간단한 형태로, 운동의 방향과 정렬된 일정한 힘에 대해, 일은 힘의 세기와 이동한 거리의 곱과 같습니다. 만약 적용되었을 때 적용의 점의 변위 방향으로 구성 요소를 가지면 힘은 양의 일(positive work)을 한다고 말합니다. 만약 힘의 적용의 점에서 변위의 방향과 반대인 구성 요소를 가지면 힘은 음의 일(negative work)을 합니다.
예를 들어, 공이 지면 위에 있다가 떨어졌을 때, 공이 떨어질 때 중력에 의해 공에 행한 일은 양수이고, 공의 무게 (힘)에 지면까지 거리 (변위)를 곱한 것과 같습니다. 만약 공이 위쪽으로 던져지면, 그것의 무게에 의해 행한 일은 음수이고, 무게에 위쪽 방향으로의 변위를 곱한 것과 같습니다.
힘과 변위 둘 다는 벡터(vectors)입니다. 행한 일은 두 벡터의 점 곱(dot product)에 의해 제공됩니다. 힘 F가 일정하고 힘과 변위 s 사이의 각도 θ도 일정할 때, 행한 일은 다음과 같이 계산됩니다:
일은 스칼라 양(scalar quantity)이므로, 그것은 오직 크기를 가지고 방향은 없습니다. 일은 에너지를 한 장소에서 또 다른 장소로, 또는 한 형태에서 또 다른 형태로 전달합니다. 일의 SI 단위(SI unit)는 에너지에 대한 같은 단위, 줄(joule, J)입니다.
History
물리학에 대한 고대 그리스의 이해는 단순 기계의 정역학 (힘의 균형)에 국한되었고, 동역학(dynamics)이나 일의 개념은 포함하지 않았습니다. 르네상스 동안, 단순 기계(simple machines)라고 불리는 기계적 일(Mechanical Powers)의 동역학은 그것들이 적용할 수 있는 힘 외에도 하중을 얼마나 멀리 들어 올릴 수 있는지의 관점에서 연구되기 시작하여, 결국 기계적 일의 새로운 개념으로 이어졌습니다. 단순 기계의 완전한 동역학 이론은 1600년 이탈리아 과학자 갈릴레오 갈릴레이(Galileo Galilei)에 의해 Le Meccaniche (On Mechanics)에서 연구했으며, 여기에서 그는 힘 증폭기로써 기계의 놓여있는 수학적 유사성을 보여주었습니다. 그는 단순 기계가 에너지를 생성하는 것이 아니라 그것을 변환할 뿐이라고 처음으로 설명했습니다.
Etymology
막스 야마(Max Jammer)에 의한 1957년 물리학 교과서에 따르면, 용어 work는 1826년 프랑스 수학자 가스파르-귀스타브 코리올리(Gaspard-Gustave Coriolis)에 의해 "높이를 통해 들어-올린 무게"로 소개되었으며, 이는 침수된 광석 광산에서 양동이 물을 들어 올리기 위해 초기 증기 엔진을 사용하는 것을 기반으로 합니다. 프랑스 공학자이자 역사가, 르네 뒤가(Rene Dugas)에 따르면, "현재 역학에서 사용되고 있다는 의미에서 work라는 용어를 사용하게 된 것"은 Solomon of Caux 덕분입니다.
비록 work가 1826년까지 공식적으로 사용되지 않았지만, 그 이전에도 유사한 개념이 존재했습니다. 1759년에, John Smeaton은 "power"라고 부르는 양을 "힘, 중력, 충격, 또는 압력의 작용을 나타내어 움직임을 생성하는 것"이라고 설명했습니다. Smeaton은 계속해서 "올려진 무게에 주어진 시간에 들어 올릴 수 있는 높이를 곱하면" 이 양을 계산할 수 있으며, 이 정의는 코리올리의 정의와 매우 유사합니다.
개념의 이름이 "work"로 정하기 전에는, 같은 개념에 대한 다른 이름으로 moment of activity, quantity of action, latent live force, dynamic effect, efficiency, 및 심지어 force까지 포함되었습니다.
Units
일의 SI 단위는 19세기 영국 물리학자 제임스 프레스콧 줄(James Prescott Joule)의 이름을 따서 지은 줄(joule, J)로, 1미터 변위를 통해 1뉴턴(newton)의 힘을 발휘하는 데 필요한 일로 정의됩니다.
차원적으로 동등한 뉴턴-미터(newton-metre, N⋅m)는 때때로 일에 대해 측정 단위로 사용되지만, 이것은 토크(torque)의 측정 단위와 혼동될 수 있습니다. N⋅m의 사용은 뉴턴-미터로 표시된 양이 토크 측정인지, 일의 측정 인지에 대해 혼동을 일으킬 수 있기 때문에 SI 기관에서 권장하지 않습니다.
일의 비-SI 단위에는 뉴턴-미터, 에르그(erg), 풋-파운드(foot-pound), 풋-파운달(foot-poundal), 킬로와트-시(kilowatt hour), 리터-대기압(litre-atmosphere), 및 마력-시(horsepower-hour)가 포함됩니다. 열과 같은 물리적 차원(physical dimension)을 가지는 일로 인해, 열(therm), BTU, 및 칼로리(calorie)와 같이 전형적으로 열 또는 에너지 함량에 대해 예약된 측정 단위가 측정하는 단위로 사용되는 경우가 있습니다.
Work and energy
힘의 방향으로 직선으로 변위 s를 이동시키는 점에서 크기 F의 일정한 힘이 한 일 W는 그것들의 곱입니다:
예를 들어, 10뉴턴 (F = 10 N)의 힘이 2미터 (s = 2 m)를 이동하는 지점을 따라 작용하면, W = Fs = (10 N) (2 m) = 20 J입니다. 이것은 근사적으로 중력에 대항하여 지면에서 사람의 머리 위로 1kg의 물체를 들어 올리는 일입니다.
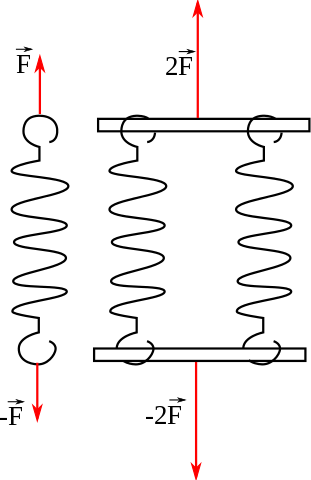
일은 같은 거리를 두 배의 무게를 들어 올리거나 같은 무게를 두 배의 거리를 들어 올리면 두 배가 됩니다.
일은 에너지(energy)와 밀접한 관련이 있습니다. 일-에너지 원리는 강체의 운동 에너지에서 증가는 강체에 작용하는 결과 힘에 의해 강체에 같은 양의 일이 가해짐에 따라 발생한다고 설명합니다. 반대로, 운동 에너지에서 감소는 결과 힘이 행한 같은 양의 음의 일로 인해 발생합니다. 따라서, 만약 알짜 일이 양수이면, 입자의 운동 에너지는 일의 양만큼 증가합니다. 만약 행한 알짜 일이 음수이면, 입자의 운동 에너지는 일의 양만큼 감소합니다.
뉴턴의 두 번째 법칙(Newton's second law)으로부터, 자유 (필드 없음), 강체 (내부 자유도 없음)에 작용하는 일은 해당 물체의 선형 속도와 각 속도(angular velocity)에 해당하는 운동 에너지
퍼텐셜 함수에 의해 생성된 힘의 일은 퍼텐셜 에너지(potential energy)로 알려져 있고 그 힘은 보존적(conservative)이라고 말합니다. 그러므로, 속도나 회전에서 변화 없이 보존적 힘 필드(field) 내에서 변위된 물체에 대한 일은 물체의 퍼텐셜 에너지 변화
이들 공식은 일이 힘의 작용과 관련된 에너지임을 보여 주므로, 일은 에너지의 물리적 차원(physical dimensions)과 단위를 가집니다. 여기서 논의된 일/에너지 원리는 전기적 일/에너지 원리와 동일합니다.
Constraint forces
구속력은 시스템에서 물체의 변위를 결정하여, 범위 내에서 그것을 제한합니다. 예를 들어, 경사(slope)와 중력이 같이 있는 경우에서, 물체는 경사면에 달라붙어 있고, 팽팽한 끈에 부착될 때, 끈을 '팽팽하게' 만들기 위해 바깥쪽으로 이동할 수 없습니다. 그것은 해당 방향의 모든 변위를 제거하며, 즉, 구속 방향에서 속도는 구속력이 시스템에서 일을 수행하지 않도록 영으로 제한됩니다.
기계 시스템(mechanical system)에 대해, 구속력은 구속 조건을 특징짓는 방향으로의 이동을 제거합니다. 따라서 구속의 힘에 의해 행한 가상 일(virtual work)은 영이며, 마찰 힘이 제외되는 경우에만 참인 결과입니다.
움직임과 구속력 사이의 각도가 항상 90°이기 때문에, 고정되고 마찰-없는 구속력은 시스템에서 일을 수행하지 않습니다. 일-없는 구속 조건의 예제는 입자 사이의 견고한 상호 연결, 마찰-없는 표면에서의 미끄러짐 동작, 및 미끄러지지 않는 구름 접촉입니다.
예를 들어, 애트우드 기계(Atwood machine)와 같은 도르래 시스템에서, 로프와 지지 도르래에서 내부 힘은 시스템에 일을 하지 않습니다. 그러므로, 일은 물체에 작용하는 중력에 대해서만 계산될 필요가 있습니다. 또 다른 예제는 옆으로 균등 원형 운동(circular motion)을 하는 공에 끈에 의해 안쪽으로 가해지는 구심력(centripetal force)이 공을 원형 운동으로 제한하여 원의 중심에서 멀어지는 움직임을 제한하는 것입니다. 이 힘은 공의 속도에 수직이기 때문에 일을 하지 않습니다.
하전 입자에 대한 자기력(magnetic force)은 F = qv × B이며, 여기서 q는 전하, v는 입자의 속도, 및 B는 자기 필드(magnetic field)입니다. 교차 곱(cross product)의 결과는 항상 두 원래 벡터 둘 다에 수직이므로, F ⊥ v입니다. 두 수직 벡터의 점 곱(dot product)은 항상 영이므로, 일 W = F ⋅ v = 0이고, 자기력은 일을 하지 않습니다. 그것은 운동의 방향을 바꿀 수 있지만 속력은 바꿀 수 없습니다.
Mathematical calculation
움직이는 물체에 대해, 일/시간 (일률)의 양은 힘의 적용의 점의 궤적을 따라 적분됩니다. 따라서, 임의의 순간에서, 힘에 의해 행한 일의 율 (줄/초, 또는 와트에서 측정)은 힘 (벡터)과 적용의 점의 속도 벡터의 스칼라 곱(scalar product)입니다. 힘과 속도의 이 스칼라 곱은 순간 일률(power)이라고 알려져 있습니다. 총 거리를 얻기 위해 시간에 걸쳐 속도를 적분할 수 있는 것처럼, 미적분의 기본 정리에 의해, 총 일은 적용의 점의 궤적을 따라 적용되는 순간 일률의 시간-적분과 유사합니다.
일은 매 순간에 속도 v를 갖는 곡선 X를 따르는 점에 작용하는 힘의 결과입니다. 순간 시간 dt 동안 발생하는 소량의 일 δW는 다음과 같이 계산됩니다:
여기서 F ⋅ v는 순간 dt에 걸쳐 일률입니다. 점의 궤적에 걸쳐 이들 소량의 일의 합은 일을 산출합니다:
여기서 C는
힘이 항상 이 직선을 따라 향하고, 힘의 크기가 F이면, 이 적분은 다음과 같이 단순화됩니다:
여기서 s는 직선을 따른 변위입니다. 만약 직선을 따라 방향화되는 것 외에도 F가 일정하고, 적분은 다음과 같이 더 단순화됩니다:
여기서 s는 직선을 따라 점의 변위입니다.
이 계산은 입자가 뒤따르는 직선을 따라 향하지 않는 일정한 힘에 대해 일반화될 수 있습니다. 이 경우에서 점 곱(dot product) F ⋅ ds = F cos θ ds이며, 여기서 θ는 힘 벡터와 이동 방향 사이의 각도이며, 즉
힘 성분이 물체의 변위에 수직일 때 (예를 들어, 물체가 중심력 아래 원형 경로를 따라 움직일 때), 90°의 코사인이 영이기 때문에 일은 수행되지 않습니다. 따라서, 원형 궤도를 갖는 행성에서는 중력에 의해 어떤 일도 수행할 수 없습니다 (이것은 이상적인데, 왜냐하면 모든 궤도가 약간 타원형이기 때문입니다). 역시, 마찰-없는 이상적인 원심분리기에서 일정한 속력으로 움직이는 것과 같이 기계적 힘에 구속되어 일정한 속력으로 원형 운동을 하는 물체에는 어떠한 일도 하지 않습니다.
Work done by a variable force
일을 "힘 곱하기 직선 경로 구획"으로 계산하는 것은 위에서 언급한 것처럼 가장 단순한 상황에서만 적용됩니다. 만약 힘이 변하거나, 물체가 구부러진 경로를 따라 이동하여, 회전할 수 있고 반드시 굳을 필요가 없으면, 힘의 적용의 점 경로만 행한 일과 관련이 있고, 적용 점 속도와 평행한 힘의 성분만 일을 하고 있습니다 (같은 방향일 때 양의 일, 속도의 반대 방향일 때 음의 일). 이 힘의 성분은 스칼라 접선 성분(scalar tangential component, F cos(θ), 여기서 θ는 힘과 속도 사이의 각도임)이라는 스칼라 양으로 설명될 수 있습니다. 그리고 그때에 가장 일반적인 일의 정의는 다음과 같이 형식화될 수 있습니다:
힘의 일은 적용의 점의 경로를 따라 스칼라 접선 성분의 선적분입니다."
만약 힘이 변하면 (예를 들어, 스프링 압축), 우리는 행한 일을 찾기 위해 미적분을 사용할 필요가 있습니다. 만약 힘이 F(x) (x의 함수)로 주어지면, a에서 b까지 x-축을 따라 힘에 의해 행한 일은 다음과 같습니다:
Torque and rotation
힘 한-쌍(force couple)은 강체의 서로 다른 두 점에 작용하는 같고 반대인 힘의 결과입니다. 이들 힘의 합 (결과)은 취소될 수 있지만, 물체에 미치는 영향은 한-쌍 또는 토크 T입니다. 토크의 일은 다음과 같이 계산됩니다:
여기서 T ⋅ ω는 순간 dt에 걸쳐 일률입니다. 강체의 궤적에 걸쳐 이러한 소량의 일의 합은 일을 산출합니다:
이 적분은 시간에 따라 변하는 각속도 ω로 강체의 궤적을 따라 계산되고, 따라서 경로 종속적(path dependent)이라고 말합니다.
만약 각속도 벡터가 일정한 방향을 유지하면, 다음과 같은 형식을 취합니다:
여기서
여기서 C는
만약 토크

이 결과는 그림과 같이 거리
토크 τ = Fr을 도입하여, 위에서 제시된 바와 같이 다음을 얻습니다:
각속도 벡터 방향에서 토크 성분만 일에 기여한다는 점에 유의하십시오.
Work and potential energy
힘 F과 그것의 적용의 점의 속도 v의 스칼라 곱은 한 순간에 시스템에 입력되는 일률(power)을 정의합니다. 적용의 점의 궤적에 대한 이 힘의 적분, C = x(t)는 힘에 의해 시스템에 입력되는 일을 정의합니다.
Path dependence
그러므로, 곡선 C를 따라 이동하는 물체에 힘 F에 의해 행한 일은 다음 선적분(line integral)으로 표시됩니다:
여기서 dx(t)는 궤적 C를 정의하고 v는 이 궤적을 따른 속도입니다. 일반적으로 이 적분은 속도가 정의되는 경로를 필요로 하므로, 일의 평가는 경로 종속적이라고 말합니다.
일에 대한 적분의 시간 도함수는 순간 일률을 산출합니다,
Path independence
만약 적용된 힘에 대한 일이 경로와 독립적이면, 그래디언트 정리(gradient theorem)에 의해, 힘에 의해 행한 일은 적용의 점의 궤적의 시작과 끝에서 평가되는 퍼텐셜 함수를 정의합니다. 이것은 이들 두 점 사이의 임의의 궤적에 걸쳐 일을 얻기 위해 두 점
함수 U(x)는 적용된 힘과 결합된 퍼텐셜 에너지(potential energy)라고 불립니다. 그러한 퍼텐셜 함수에서 파생된 힘은 보존적(conservative)이라고 말합니다. 퍼텐셜 에너지를 가지는 힘의 예로는 중력과 스프링 힘이 있습니다.
이 경우에서, 일의 그래디언트(gradient)는 다음을 산출합니다:
그리고 힘 F는 "퍼텐셜에서 유도-가능"이라고 말합니다.
퍼텐셜 U는 공간에서 모든 각 점 x에서 힘 F를 정의하기 때문에. 힘의 집합은 힘 필드(force field)라고 불립니다. 힘 필드에 의해 물체에 가해지는 힘은 물체의 속도 V의 방향에서 일 또는 퍼텐셜의 그래디언트에서 얻습니다. 즉,
Work by gravity

다른 힘이 없을 때, 중력은 자유롭게 움직이는 모든 각 물체의 아래-방향 가속도를 일정하게 만듭니다. 지구 표면 근처에서, 중력으로 인한 가속도는
만약 무게 mg를 갖는 물체가 수직 거리
여기서
Work by gravity in space
질량 M에 의해 또 다른 질량 m에 가하는 중력은 다음과 같이 주어집니다:
여기서 r은 M에서 m까지의 위치 벡터이고
질량 m이 속도 v에서 움직인다고 놓습니다; 그런-다음 위치
질량 m의 위치와 속도는 다음과 같이 주어짐에 주목하십시오:
여기서
이 계산은 다음 사실을 사용합니다:
다음 함수는
중력 퍼텐셜 에너지(gravitational potential energy)라고도 하는 중력 퍼텐셜 함수입니다. 음의 부호는 퍼텐셜 에너지의 손실에서 일을 얻는다는 관례를 따른 것입니다.
Work by a spring
몸체가 움직이는 방식과 관계없이 x 방향에서 그것의 처짐에 비례하는 수평 힘 F = (−kx, 0, 0)를 가하는 스프링을 생각해 보십시오. 곡선 X(t) = (x(t), y(t), z(t))와 함께 공간을 따라 이동하는 물체에 대한 이 스프링의 일은 그것의 속도
편의를 위해, t = 0에서 스프링과의 접촉이 발생하고, 시간 t에 걸쳐 거리 x와 x-속도
Work by a gas
기체의 그것의 둘러싼 몸체에 의해 행한 일
여기서 P는 압력, V는 부피이고, a와 b는 초기 부피와 최종 부피입니다.
Work–energy principle
일과 운동 에너지(kinetic energy)의 원리 (일-에너지 원리라고도 알려져 있음)는 입자에 작용하는 모든 힘에 의해 행한 일 (결과 힘의 일)은 입자의 운동 에너지에서 변화와 같다고 말합니다. 즉, 입자(particle)에 작용하는 결과 힘(resultant force)에 의해 행한 일 W는 입자의 운동 에너지
여기서
일-에너지 원리의 유도는 뉴턴의 운동의 두 번째 법칙과 입자에 미치는 결과 힘으로 시작됩니다. 힘의 스칼라 곱과 입자 속도의 계산은 시스템에 추가된 순간 일률을 평가합니다. (구속 조건은 구속력의 방향으로 속도 성분이 없음을 보증함으로써 입자의 운동의 방향을 정의합니다. 이것은 역시 구속력이 순시 일률에 추가되지 않는다는 것을 의미합니다.) 이 스칼라 방정식의 시간 적분은 순간 일률에서 일을 산출하고, 운동 에너지는 가속도와 속도의 스칼라 곱에서 얻습니다. 일-에너지 원리가 구속력을 제거한다는 사실은 라그랑주 역학(Lagrangian mechanics)의 기초가 됩니다.
이 섹션은 입자 동역학에 적용되는 것처럼 일-에너지 원리에 초점을 맞춥니다. 보다 일반적인 시스템에서, 일은 기계 장치의 퍼텐셜 에너지(potential energy), 열 시스템의 열 에너지, 또는 전기 장치의 전기 에너지(electrical energy)를 변경할 수 있습니다. 일은 에너지를 한 장소에서 또 다른 장소로 또는 한 형태에서 또 다른 형태로 전달합니다.
Derivation for a particle moving along a straight line
결과 힘(resultant force) F가 크기와 방향이 모두 일정하고, 입자의 속도와 평행하면, 입자는 일정한 가속도 a로 직선을 따라 움직입니다. 알짜 힘과 가속도 사이의 관계는 방정식 F = ma (뉴턴의 두 번째 법칙)로 주어지고, 입자 변위(displacement) s는 다음 방정식으로 표현될 수 있습니다:
이는
알짜 힘의 일은 그 크기와 입자 변위의 곱으로 계산됩니다. 위의 방정식을 대입하면, 다음을 얻을 수 있습니다:
다른 유도:
일반적인 직선 운동의 경우에서, 알짜 힘 F의 크기가 일정하지 않고, 방향이 일정하고, 입자의 속도와 평행할 때, 일은 입자의 경로를 따라 적분되어야 합니다:
General derivation of the work–energy principle for a particle
임의의 곡선 경로를 따라 움직이는 입자에 작용하는 임의의 알짜 힘에 대해, 일은 위의 방정식과 유사한 간단한 유도를 통해 입자의 운동 에너지에서 변화와 같음을 시연할 수 있습니다. 그것은 일-에너지 원리로 알려져 있습니다:
항등식
위의 유도의 남아있는 부분은 앞선 직선의 경우와 마찬가지로 단순한 미적분입니다.
Derivation for a particle in constrained movement
입자 동역학에서, 시스템에 적용되는 일과 그것의 운동 에너지에서 변화를 동일시하는 공식은 뉴턴의 운동의 두 번째 법칙의 첫 번째 적분으로 구합니다. 뉴턴의 법칙에 사용되는 결과 힘은 입자에 적용되는 힘과 입자의 움직임에 대한 구속에 의해 부과되는 힘으로 분리될 수 있다는 점을 알아두는 것이 유용합니다. 놀랍게도, 구속력의 일은 영이며, 그것에 의해 일-에너지 원리에서는 적용된 힘의 일만 고려되어야 합니다.
이를 확인하려면, 그것에 작용하는 힘 F를 갖는 궤적 X(t)를 따르는 입자 P를 생각해 보십시오. 입자를 환경에서 분리하여 구속력 R을 노출하면, 뉴턴의 법칙은 다음과 같은 형식을 취합니다:
여기서 m은 입자의 질량입니다.
Vector formulation
벡터 위의 n개의 점은 n번째 시간 도함수(time derivative)를 나타냅니다. 뉴턴의 법칙 각 변과 속도 벡터의 스칼라 곱(scalar product)은 다음을 산출합니다:
왜냐하면 구속력이 입자 속도에 수직이기 때문입니다. 점
이 방정식의 왼쪽 변은 시간
이 적분은 입자의 궤적 X(t)를 따라 계산되고 따라서 경로 의존적입니다.
뉴턴 방정식의 첫 번째 적분의 오른쪽 변은 다음 항등식을 사용하여 단순화될 수 있습니다:
(유도에 대해 곱 규칙(product rule)을 참조하십시오). 이제 그것은 운동 에너지에서 변화를 얻기 위해 명시적으로 적분됩니다:
여기서 입자의 운동 에너지는 스칼라 양으로 정의되며,
Tangential and normal components
속도와 가속도 벡터를 다음임을 만족하는 궤적 X(t)를 따라 접선 성분과 법선 성분으로 해석하는 것이 유용합니다:
여기서
그런-다음, 뉴턴의 두 번째 법칙에서 가속도와 속도의 스칼라 곱(scalar product)은 다음 형식을 취합니다:
여기서 입자의 운동 에너지는 스칼라 양으로 정의되며,
그 결과는 입자 동역학의 일-에너지 원리입니다,
이 유도는 임의적인 강체 시스템으로 일반화될 수 있습니다.
Moving in a straight line (skid to a stop)
구동력과 중력울 합해서 F의 작용 아래에서 직선 수평 궤적을 따라 이동하는 자동차의 경우를 생각해 보십시오. 자동차와 도로 사이의 구속력은 R을 정의하고, 다음을 가집니다:
편의를 위해, 궤적이 X-축을 따라 있다고 놓고, 따라서 X = (d, 0)이고 속도는 V = (v, 0)이면, R ⋅ V = 0이고
양쪽 변의 적분은 다음을 산출합니다:
만약
예를 들어 자동차가 미끄러져 정지했다고 생각해 보십시오, 여기서 k는 마찰 계수이고 W는 자동차의 무게입니다. 그런-다음 궤적을 따르는 힘은
이 공식은 자동차의 질량이 m = W/g라는 사실을 사용함을 주목하십시오.
Coasting down an inclined surface (gravity racing)
정지 상태에서 출발하여 경사진 표면 (예를 들어, 산비탈)을 따라 내려가는 자동차의 경우를 생각해 보십시오, 일-에너지 원리는 자동차가 속도 V, 말하자면 60 mph (88 fps)에 도달하기 위해 이동하는 최소 거리를 계산하는 데 도움이 됩니다. 회전 저항과 공기 저항은 자동차의 속도를 늦추므로 이들 힘을 무시하는 경우보다 실제 거리가 더 길어집니다.
도로를 따라가는 자동차의 궤적을 삼-차원 공간에서 곡선인 X(t)라고 놓습니다. 자동차를 도로 아래로 밀어내는 차량에 작용하는 힘은 일정한 중력 F = (0, 0, W)이고, 반면에 자동차에 대한 도로의 힘은 구속력 R입니다. 뉴턴의 두 번째 법칙은 다음을 산출합니다:
이 방정식과 속도
여기서 V는 V의 크기입니다. 차량과 도로 사이의 구속력은 R ⋅ V = 0이기 때문에 이 방정식에서 취소되며, 이는 그것들이 일을 하지 않음을 의미합니다. 다음을 얻기 위해 양쪽 변을 적분하면,
무게 힘 W는 궤적을 따라 일정하고 수직 속도의 적분은 수직 거리이며, 따라서
도로를 따라 거리를 결정하기 위해, 내려받이가 6%라고 가정하며, 이는 가파른 도로입니다. 이것은 고도가 100피트를 이동할 때마다 6피트 감소한다는 것을 의미합니다—이 작은 각도에 대해, sin 및 tan 함수는 거의 같습니다. 그러므로, 속도 V에 도달하기 위한 6% 기울기 아래로 피트 단위에서 거리 s는 적어도 다음입니다:
이 공식은 자동차의 무게가 W = mg이라는 사실을 사용합니다.
Work of forces acting on a rigid body
단일 강체의 여러 지점에서 작용하는 힘의 일은 결과 힘과 토크의 일로부터 계산될 수 있습니다. 이것을 보기 위해, 힘
궤적을 따라 점
여기서 ω는 각속도 행렬로 알려진 다음과 같은 반-대칭 행렬에서 얻은 각속도 벡터입니다:
작은 변위
또는
이 공식은 다음을 얻기 위해 다시 쓸 수 있습니다:
여기서 F와 T는 강체에서 움직이는 프레임 M의 참조 점 d에 적용되는 결과 힘과 토크입니다.
Bibliography
- Serway, Raymond A.; Jewett, John W. (2004). Physics for Scientists and Engineers (6th ed.). Brooks/Cole. ISBN 0-534-40842-7.
- Tipler, Paul (1991). Physics for Scientists and Engineers: Mechanics (3rd ed., extended version ed.). W. H. Freeman. ISBN 0-87901-432-6.
External links

