시간 도함수는 보통 함수 값의 변화율로 해석되는 시간(time)에 관한 함수의 도함수(derivative)입니다. 시간을 나타내는 변수는 보통 \(t\)로 씁니다.
Notation
다양한 표기법이 시간 도함수를 나타내기 위해 사용됩니다. 정규 (라이프니츠의) 표기법 이외에,
\(\quad\displaystyle \frac {dx} {dt}\)
특히 물리학에서 사용되는 매우 공통적인 속기 표기법은 '윗-점'입니다. 즉,
\(\quad \dot{x}\)
(이것은 [[Newton's notation|뉴턴의 표기법(Newton's notation)]]이라고 불립니다.)
고차 시간 도함수는 역시 사용됩니다: 시간에 관한 [[second derivative|이차 도함수(second derivative)]]는 다음으로 쓰입니다:
\(\quad\displaystyle \frac {d^2x} {dt^2}\)
이에 해당하는 속기 표기법은 \(\ddot{x}\)입니다.
일반화로서, 벡터의 시간 도함수는, 말하자면:
\(\quad \mathbf v = \left[ v_1,\ v_2,\ v_3, \ldots \right] \)
그것의 성분이 원래 벡터의 성분의 도함수인 벡터로 정의됩니다. 즉,
\(\quad\displaystyle \frac {d \mathbf v } {dt} = \left[ \frac{ d v_1 }{dt},\frac {d v_2 }{dt},\frac {d v_3 }{dt}, \ldots \right] . \)
Use in physics
시간 도함수는 물리학(physics)의 핵심 개념입니다. 예를 들어, 변하는 위치(position) \(x\)에 대해, 그것의 시간 도함수 \(\dot{x}\)는 속도(velocity)이고, 시간에 관한 그것의 이차 도함수, \(\ddot{x}\)는 가속도(acceleration)입니다. 심지어 더 높은 도함수가 때때로 사용됩니다: 시간에 관한 위치의 삼차 도함수는 [[Jerk (physics)|저크(jerk)]]라고 합니다. 운동 그래프와 도함수(motion graphs and derivatives)를 참조하십시오.
물리학에서 많은 기본 방정식은 양의 일차 또는 이차 도함수와 관련합니다. 과학에서 다른 많은 기본 수량은 서로의 시간 도함수입니다:
- 힘(force)은 운동량(momentum)의 시간 도함수입니다.
- 전력(power)은 에너지(energy)의 시간 도함수입니다.
- 전류(electric current)는 전하(electric charge)의 시간 도함수입니다.
이런 식으로 계속됩니다.
물리학에서 흔히 발생하는 것은 속도 또는 변위와 같은 벡터(vector)의 시간 도함수입니다. 그러한 도함수를 다룰 때, 크기와 방향은 모두 시간에 따라 달라질 수 있습니다.
Example: circular motion
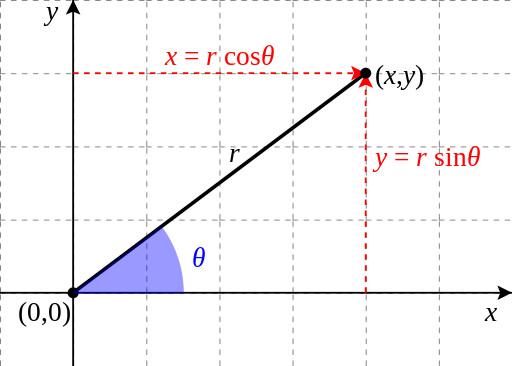
예를 들어, 원형 경로에서 움직이는 입자를 생각해 보십시오. 그것의 위치는 그림에 정의된 것처럼, 각도 θ와 방사상 거리 r과 관련된 변위 벡터 \(r=x\hat{\imath}+y\hat{\jmath}\)에 의해 제공됩니다:
\(\quad \begin{align}
x &= r \cos(\theta) \\
y &= r \sin(\theta)
\end{align}\)
이 예제에 대해, 우리는 θ = t임을 가정합니다. 따라서, 임의의 시간 t에서 변위 (위치)는 다음에 의해 제공됩니다:
\(\quad \mathbf{r}(t) = r\cos(t)\hat{\imath}+r\sin(t)\hat{\jmath}\)
이 형식은 r(t)에 의해 설명된 운동이 r(t)의 크기가 다음에 의해 제공되기 때문에 반지름 r의 원 안에 있음을 보입니다:
\(\quad|\mathbf{r}(t)| = \sqrt{\mathbf{r}(t) \cdot \mathbf{r}(t)}=\sqrt {x(t)^2 + y(t)^2 } = r\, \sqrt{\cos^2(t) + \sin^2(t)} = r\)
이때, 삼각 항등식(trigonometric identity) \(\sin^2(t)+\cos^2(t)=1\)을 사용하고 여기서 \(\cdot\)는 보통의 유클리드 점 곱입니다.
변위에 대한 이 형식과 함께, 속도는 이제 구해집니다. 변위 벡터의 시간 도함수는 속도 벡터입니다. 일반적으로, 벡터의 도함수는 각각이 원래 벡터의 해당 성분의 도함수인 성분으로 구성된 벡터입니다. 따라서, 이 경우에서, 속도 벡터는 다음과 같습니다:
\(\quad\displaystyle
\begin{align}
\mathbf{v}(t) = \frac {d\,\mathbf{r}(t) }{dt} &= r \left[\frac{d\, \cos(t)}{dt}, \frac{d\, \sin(t)}{dt} \right] \\
&= r\ [ -\sin(t),\ \cos(t)] \\
&= [-y (t), x(t)].
\end{align}\)
따라서 입자의 속도는 심지어 위치의 크기 (즉, 경로의 반지름)가 일정하더라도 영이 아닙니다. 속도는 점 곱(dot product)을 사용하여 설정될 수 있는 것처럼 변위에 수직으로 향합니다:
\(\quad \mathbf{v} \cdot \mathbf{r} = [-y, x] \cdot [x, y] = -yx + xy = 0\, . \)
가속도는 그런-다음 속도의 시간-도함수입니다:
\(\quad\displaystyle \mathbf{a}(t) = \frac {d\, \mathbf{v}(t)}{dt} = [-x(t), -y(t)] = -\mathbf{r}(t)\, .\)
가속도는 회전축을 향해 안쪽으로 향합니다. 그것은 위치 벡터와 반대 방향을 가리키고 속도 벡터에 수직입니다. 이 안쪽으로 향하는 가속도를 구심 가속도(centripetal acceleration)라고 합니다.
In differential geometry
미분 기하학(differential geometry)에서, 양은 종종 지역 공변 기저(covariant basis) \(\mathbf{e}_i \)에 관해 표현될 수 있으며, 여기서 i는 차원의 숫자에 걸쳐 변합니다. 이 방법에 의해 표현된 벡터 \(\mathbf{U} \)의 성분은 아인슈타인 합계 관례(Einstein summation convention)라고 부르는 표현 \(\mathbf{U}=U^i\mathbf{e}_i \)에서 보인 것처럼 반변 텐서(tensor)로 변환합니다. 만약 우리가 \(\mathbf{U}(t)=U^i(t)\mathbf{e}_i(t) \)을 가지도록 궤적을 따라 이들 성분의 시간 도함수를 계산하기를 원하면, 우리는 새로운 연산자, 불변 도함수 \(\delta \)를 정의할 수 있으며, 이것은 반변 텐서를 계속 반환할 것입니다:
\(\quad \begin{align}
\frac{\delta U^i}{\delta t}
= \frac{d U^i}{d t} + V^j\Gamma^i_{jk} U^k \\
\end{align}\)
여기서 \(V^j=\frac{d x^j}{d t} \) (\(x^j\)는 ''j''번째 좌표임)는 지역 공변 기저에서 속도의 성분을 포획하고, \( \Gamma^i_{jk} \)는 좌표 시스템에 대해 리스토펠 기호(Christoffel symbols)입니다. t에 대한 명시적 종속성은 표기법에서 억제되었습니다. 우리는 그런-다음 다음과 같이 쓸 수 있습니다:
\(\quad \begin{align}
\frac{d \mathbf{U}}{d t}
= \frac{\delta U^i}{\delta t} \mathbf{e}_i \\
\end{align}\)
마찬가지로:
\(\quad \begin{align}
\frac{d^2 \mathbf{U}}{d t^2}
= \frac{\delta^2 U^i}{\delta t^2} \mathbf{e}_i \\
\end{align}\)
공변 도함수(covariant derivative), \(\nabla_{j}\)의 관점에서, 우리는 다음을 가집니다:
\(\quad \begin{align}
\frac{\delta U^i}{\delta t}
= V^j \nabla_{j} U^i \\
\end{align}\)
Use in economics
경제학(economics)에서, 다양한 경제 변수의 진화의 많은 이론적 모델은 연속 시간(continuous time)에서 구성되고 따라서 시간 도함수를 사용합니다. 한 가지 상황은 스톡 변수(stock variable)와 그것의 시간 도함수, 플로우 변수(flow variable)를 포함합니다. 예제는 다음을 포함합니다:
- 순 고정 투자(fixed investment)의 플로우는 자본 스톡(capital stock)의 시간 도함수입니다.
- 재고 투자(inventory investment)의 플로우는 재고(inventories)의 스톡의 시간 도함수입니다.
- 화폐 공급(money supply)의 성장률은 화폐 공급의 시간 도함수를 화폐 공급 자체로 나눈 값입니다.
때때로 플로우 변수의 시간 도함수는 다음 모델에서 나타날 수 있습니다:
- 산출량(output) 증가율은 산출량 흐름의 시간 도함수를 산출량 자체로 나눈 값입니다.
- 노동력(labor force)의 성장률은 노동력의 시간 도함수를 노동력 자체로 나눈 값입니다.
그리고 때때로 위의 예제와 달리 통화 단위로 측정되지 않는 변수의 시간 도함수가 나타납니다:
- 주요 이자율(interest rate)의 시간 도함수가 나타날 수 있습니다.
- 인플레이션율(inflation rate)은 물가 수준(price level)의 성장률–즉 물가 수준의 시간 도함수를 물가 수준 자체로 나눈 값입니다.
See also
References
- Chiang, Alpha C., Fundamental Methods of Mathematical Economics, McGraw-Hill, third edition, 1984, ch. 14, 15, 18.
- Grinfeld, Pavel. "Tensor Calculus 6d: Velocity, Acceleration, Jolt and the New δ/δt-derivative". Archived from the original on 2021-12-13.
- See for example Romer, David (1996). Advanced Macroeconomics. McGraw-Hill. ISBN 0-07-053667-8.


