
수학(mathematics)에서, 역함수(inverse function) (또는 반대-함수(anti-function))는 또 다른 함수를 "뒤집는(reverse)" 함수(function)입니다: 만약 입력 x에 적용된 함수 f가 y의 결과를 제공하면, 그의 역함수 g에 y를 적용하는 것은 결과 x를 제공하고, 그 반대도 마찬가지입니다. 즉, f(x) = y인 것과 g(y) = x인 것은 필요충분(iff) 조건입니다.
예제로써, f(x) = 5x − 7로 주어지는 실수 변수의 실수-값(real-valued) 함수를 생각해 보십시오. 단계별 절차로 이것을 생각하면 (즉, 숫자 x를 취하고, 그것에 5를 곱하고, 그런-다음 결과에서 7을 뺍니다), 이것을 뒤집고 어떤 출력 값, 말하자면 y로부터 x를 역으로 얻기 위해, 우리는 각 단계를 역순으로 취소해야 합니다. 이 경우에서 우리는 y에 7을 더하고 그런-다음 결과를 5로 나누어야 함을 의미합니다. 함수 표기법에서 이 역함수는 다음과 같이 제공될 것입니다:
\(\quad\)\(\displaystyle g(y)=\frac{y+7}{5}\).
y = 5x − 7과 함께, 우리는 f(x) = y 및 g(y) = x임을 가집니다.
모든 함수가 역함수를 갖는 것은 아닙니다; 역함수를 가지는 것들은 역-가능(invertible)으로 불립니다. 함수 f: X → Y에 대해 역을 구하기 위해, 그것은 Y에서 모든 각 y에 대해 f(x) = y가 되도록 X에서 반드시 하나, 및 오직 하나의 x가 있어야 하는 속성을 반드시 가져야 합니다. 이 속성은 함수 g: Y → X가 f와 필요한 관계를 가지고 존재할 것임을 보증합니다.
Definitions

f를 그의 도메인(domain)이 집합(set) X이고, 그의 이미지(image)가 집합 Y인 함수로 놓습니다. 그런-다음 f가, 만약 도메인 Y 및 이미지 X를 갖고 다음 속성을 갖는 함수 g가 존재하면, 역-가능입니다:
\(\quad\)\(f(x) = y\,\,\Leftrightarrow\,\,g(y) = x.\)
만약 f가 역-가능이면, 함수 g는 유일(unique)하며, 이것은 이 속성을 만족시키는 함수 g가 (덜도 말고, 더도 말고) 정확하게 하나 있습니다. 해당 함수 g는, 그런-다음, f의 그 역으로 불리고, 보통 \(f^{-1}\)로 표시됩니다.
달리 말하면, 이항 관계(binary relation)로 여겨진 함수는 역을 가진 것과 전환 관계(converse relation)가 치역 Y 위에 함수인 것은 필요충분 조건이며, 이 경우에서 전환 관계는 역 함수입니다.
모든 함수가 역을 가지는 것은 아닙니다. 역을 갖기 위한 함수에 대해, 각 y ∈ Y는 반드시 하나보다 많지 않은 x ∈ X에 대응해야 합니다; 이 속성을 가진 함수 f를 일-대-일 또는 단사(injection)로 불립니다. 만약 \(f^{-1}\)가 Y의 함수(function)이면, 각 원소 y ∈ Y는 반드시 일부 x ∈ X와 대응해야 합니다. 이 속성을 가진 함수는 전사(surjections)로 불립니다. 이 속성은, 만약 Y가 f의 이미지 (치역)이면, 정의에 의해 만족시키지만, 보다 일반적인 문맥에서 유지되지 않을 수 있습니다. 역-가능이 되기 위해, 함수는 단사와 전사 둘 다여야 합니다. 그러한 함수는 전단사(bijections)로 불립니다. 전단사가 아닌 단사 f: X → Y의 역, 즉, 전사가 아닌 함수는 Y에서 오직 부분 함수(partial function)이며, 이것은 일부 y ∈ Y에 대해, \(f^{-1}(y)\)가 정의되지 않음을 의미합니다. 만약 함수 f가 역-가능이면, 그것과 그의 역 함수 \(f^{-1}\) 둘 다는 전단사입니다.
함수 정의에 사용되는 또 다른 관례가 있습니다. 이것은 코도메인(codomain)이 절대 참조되지 않는 순서 쌍(ordered pair)을 사용하여 "집합-이론적" 또는 "그래프" 정의로 참조될 수 있습니다. 이 관례 아래에서 모든 함수는 전사이고, 그러므로 전단사인 것은 단순히 단사인 것을 의미입니다. 이 관례를 사용하는 저자는 함수가 역-가능이라는 문구와 그것이 단사인 것은 필요충분 조건으로 사용할 수 있습니다. 두 관례는, 이 대체 관례에서 함수의 코도메인이 항상 함수의 치역인 것을 취한다는 것을 기억하는 한, 혼동을 일으킬 가능성이 없습니다.
Example: Squaring and square root functions
\(f(x)=x^2\)으로 주어진 함수 f: ℝ → [0,∞)는 단사가 아닌데 왜냐하면 각 가능한 결과 y (0 제외)가 X에서 두 다른 시작하는 점에 해당하기 때문입니다 – 하나의 양수 및 하나의 음수, 및 그래서 이 함수는 역-가능이 아닙니다. 함수의 이 유형과 함께 출력으로부터 입력을 추론하는 것은 불가능입니다. 그러한 함수는 비-단사(injective), 또는 일부 응용에서, 정보-손실로 불립니다.
만약 함수의 도메인이 비-음의 실수로 제한되면, 즉 함수가 이전처럼 같은 규칙과 함께 f: [0, ∞) → [0, ∞)로 재정의되면, 함수는 전단사이고, 그러므로 역-가능입니다. 역함수는 여기서 (양의) 제곱근 함수로 불립니다.
Inverses and composition
만약 f는 도메인 X와 치역 Y와 함께 역-가능 함수이면, 다음입니다:
\(\quad\)\( f^{-1}\left( \, f(x) \, \right) = x\), for every \(x \in X. \)
함수의 합성(composition of functions)을 사용하여 우리는 다음으로 이 명제를 다시-쓸 수 있습니다:
\(\quad\)\( f^{-1} \circ f = \operatorname{id}_X, \)
여기서 \(\operatorname{id}_X\)는 집합 X 위의 항등 함수(identity function)입니다; 즉, 그의 인수를 변경 없이 남겨두는 함수입니다. 카테고리 이론(category theory)에서, 이 명제는 역 사상(morphism)의 정의로 사용됩니다.
함수 합성을 고려하는 것은 표기법 \(f^{-1}\)을 이해하는 데 도움이 됩니다. 함수와 자체를 반복적으로 합성하는 것은 반복(iteration)으로 불립니다. 만약 f가 값 x로 시작하여 n-번 적용되면, 이것은 \(f^{n}(x)\)으로 쓰입니다; 그래서 \(f^2(x)=f(f(x))\), 등입니다. \(f^{-1}(f(x))=x\)이므로 \(f^{-1}\) 및 \(f^{n}\)을 합성하면 \(f^{n-1}\)을 산출하며, f의 하나의 적용의 효과를 "실행 취소"합니다.
Notation
표기법 \(f^{-1}(x)\)은 오해될 수 있지만, \((f(x))^{-1}\)은 확실히 f(x)의 곱셈의 역(multiplicative inverse)를 나타내고 f의 역 함수와는 아무런 관련이 없습니다.
일반적인 표기법 유지에서, 일부 영국의 저자는 \(\sin^{-1}(x)\)와 같은 표현을 x에 적용된 사인 함수의 역을 나타내기 위해 사용합니다 (실제로는 부분 역(partial inverse); 아래를 참조하십시오); 다른 저자는 이것이 \((\sin(x))^{-1}\)로 표시될 수 있는 \(\sin(x)\)의 곱셈의 역에 대한 표기법과 혼동될 수 있습니다. 혼동을 피하기 위해, 역 삼각 함수(inverse trigonometric function)는 종종 접두사 "arc" (라틴어 arcus에 대해)로 표시됩니다. 예를 들어, 사인 함수의 역은 전형적으로 arcsin(x)로 쓰는 아크사인(arcsine) 함수로 불립니다. 마찬가지로, 쌍곡선 함수(hyperbolic function)의 역은 접두사 "ar" (라틴어 area에 대해)로 표시됩니다. 예를 들어, 쌍곡 사인(hyperbolic sine) 함수의 역은 전형적으로 arsinh(x)로 쓰입니다. 다른 역 특수 함수는, 만약 \(f^{-1}\) 표기법의 모호성이 반드시 피해져야 한다면, 때때로 접두사 "inv"를 앞에 붙입니다.
Properties
함수는 이항 관계(binary relation)의 특수 유형이므로, 역 함수의 많은 속성은 전환 관계(converse relation)의 속성에 해당합니다.
Uniqueness
만약 역함수가 주어진 함수 f에 대해 존재하면, 그것은 고유합니다. 이것은 역함수가 f에 의해 완전히 결정되는 전환 관계여야 하므로 따릅니다.
Symmetry
함수와 그의 역 사이는 대칭이 있습니다. 구체적으로, 만약 f가 도메인 X와 치역 Y를 갖는 역-가능한 함수이면, 그의 역 \(f^{-1}\)는 도메인 Y와 치역 X를 갖고, \(f^{-1}\)의 역은 원래 함수 f입니다. 기호에서, 함수 \(f : X \to Y\) 및 \(f^{-1} : Y \to X\)에 대해,
\(\quad\)\(f^{-1}\circ f = \operatorname{id}_X \) and \( f \circ f^{-1} = \operatorname{id}_Y.\)
이 명제는 f에 대해 역-가능이기 위해 그것이 전단사여야 함인 함축의 결과이다. 역의 인볼루션(involutory) 본성은 간결하게 다음에 의해 표현될 수 있습니다:
\(\quad\)\(\left(f^{-1}\right)^{-1} = f.\)

함수의 합성의 역은 다음에 의해 제공됩니다:
\(\quad\)\((g \circ f)^{-1} = f^{-1} \circ g^{-1}.\)
g 및 f의 순서가 반대로 되었음을 주목하십시오; f 다음에 g를 취소하기 위해, 우리는 먼저 g를 취소하고 그런-다음 f를 취소해야 합니다.
예를 들어, f(x) = 3x로 놓고 g(x) = x + 5로 놓습니다. 그런-다음 합성 g ∘ f은 먼저 3을 곱하고 그런-다음 5를 더하는 함수입니다:
\(\quad\)\((g \circ f)(x) = 3x + 5.\)
이 과정을 거꾸로 하기 위해, 우리는 먼저 5를 빼고, 그런-다음 삼으로 나누어야 합니다:
\(\quad\)\((g \circ f)^{-1}(x) = \tfrac13(x - 5).\)
이것은 합성 (f −1 ∘ g −1)(x)입니다.
Self-inverses
만약 X가 집합이면, X 위의 항등 함수(identity function)는 그 자신의 역입니다:
\(\quad\)\({\operatorname{id}_X}^{-1} = \operatorname{id}_X.\)
보다 일반적으로, 함수 f : X → X가 그 자신의 역과 같은 것과 합성 f ∘ f이 \(\operatorname{id}_X\)와 같은 것은 필요충분 조건입니다. 그러한 함수는 인볼루션(involution)으로 불립니다.
Inverses in calculus
단일-변수 미적분(calculus)은 주로 실수를 실수로 매핑하는 함수와 관련됩니다. 그러한 함수는 종종 다음과 같은 공식(formula)을 통해 정의됩니다:
\(\quad\)\(f(x) = (2x + 8)^3 .\)
실수에서 실수로의 전사 함수 f는 일-대-일인 한, 즉 y = f(x)의 그래프가 각 가능한 y 값에 대해 오직 하나의 대응하는 x 값을 가지고, 따라서 수평 직선 테스트(horizontal line test)를 통과하는 한 역을 소유합니다.
다음 테이블은 여러 표준 함수와 그들의 역을 보입니다:
| 함수 \(f(x)\) | 역 \(f^{-1}(y)\) | 비고 |
| \(x+a\) | \(y-a\) | |
| \(a-x\) | \(a-y\) | |
| \(mx\) | \(y/m\) | \(m \neq 0\) |
| \(1/x\) (즉, \(x^{-1}\)) | \(1/y\) (즉, \(y^{-1}\)) | \(x,y \neq 0\) |
| \(x^2\) | \(\sqrt{y}\) (즉, \(y^{1/2}\)) | 오직 \(x,y \ge 0\) |
| \(x^3\) | \(\sqrt[3]{y}\) (즉, \(y^{1/3}\)) | \(x\)와 \(y\)에 대한 제한 없음. |
| \(x^p\) | \(\sqrt[p]{y}\) (즉, \(y^{1/p}\)) | 만약 \(p\)가 짝수이면, \(x,y \ge 0\); 정수 \(p > 0\) |
| \(2^x\) | \(\rm{lb} y\) | \(y > 0\) |
| \(e^x\) | \(\ln y\) | \(y > 0\) |
| \(10^x\) | \(\log y\) | \(y > 0\) |
| \(a^x\) | \(\log_a y\) | \(y > 0\)와 \(a > 0\) |
| 삼각 함수 | 역 삼각 함수 | 다양한 제한 (아래 테이블을 참조하십시오) |
| 쌍곡 함수 | 역 쌍곡 함수 | 다양한 제한 |
Formula for the inverse
\(f^{-1}\)에 대해 공식을 찾기 위한 한 접근은, 만약 그것이 존재하면, x에 대해 방정식(equation) y = f(x)을 푸는 것입니다. 예를 들어, 만약 f가 다음 함수이면,
\(\quad\)\(f(x) = (2x + 8)^3 \)
우리는 x에 대해 방정식 \(y=(2x + 8)^3\)을 풀어야 합니다:
\(\quad\)\(\begin{align}
y & = (2x+8)^3 \\
\sqrt[3]{y} & = 2x + 8 \\
\sqrt[3]{y} - 8 & = 2x \\
\dfrac{\sqrt[3]{y} - 8}{2} & = x .
\end{align}\)
따라서 역 함수 \(f^{-1}\)는 다음 공식에 의해 제공됩니다:
\(\quad\)\(f^{-1}(y) = \frac{\sqrt[3]{y} - 8} 2.\)
때때로, 함수의 역은 항의 유한 숫자를 갖는 공식에 의해 절대 표현될 수 없습니다. 예를 들어, 만약 f가 다음 함수이면,
\(\quad\)\(f(x) = x - \sin x ,\)
f는 전단사이고, 그러므로 역 함수 \(f^{-1}\)를 소유합니다. 이 역에 대해 공식(formula for this inverse)은 항의 무한 숫자를 가집니다:
\(\quad\)\(\displaystyle f^{-1}(y) =
\sum_{n=1}^\infty
\frac{y^{n/3}}{n!} \lim_{ \theta \to 0} \left(
\frac{\mathrm{d}^{\,n-1}}{\mathrm{d} \theta^{\,n-1}} \left(
\frac \theta { \sqrt[3]{ \theta - \sin( \theta )} } \right)
\right).
\)
Graph of the inverse

만약 f가 역-가능이면, 함수
\(\quad\)\(y = f^{-1}(x)\)
의 그래프는 다음 방정식의 그래프와 같습니다:
\(\quad\)\(x = f(y) .\)
이것은 x와 y의 역할이 뒤바뀐 것을 제외하고, f의 그래프를 정의하는 방정식 y = f(x)와 동일합니다. 따라서, \(f^{-1}\)의 그래프는 x와 y-축의 위치를 전환함으로써 f의 그래프로부터 얻어질 수 있습니다. 이것은 직선 y = x를 가로질러 그래프를 반사하는 것(reflecting)과 동등합니다.
Inverses and derivatives
연속 함수(continuous function) f는 그의 치역 위에 역-가능인 것과 그것이 엄격하게 증가 또는 감소하는 것 (지역 최댓값 또는 최솟값이 없음)은 필요충분 조건입니다. 예를 들어, 함수
\(\quad\)\(f(x) = x^3 + x\)
는 역-가능인데, 왜냐하면 도함수(derivative) \(f'(x)=3x^2+1\)는 항상 양수이기 때문입니다.
만약 함수 f가 구간 I 위에 미분-가능(differentiable)이고 각 x ∈ I에 대해 f′(x) ≠ 0이면, 역 \(f^{-1}\)은 f(I) 위에 미분-가능일 것입니다. 만약 y = f(x)이면, 역의 도함수는 역 함수 정리(inverse function theorem)에 의해 제공됩니다:
\(\quad\)\(\displaystyle \left(f^{-1}\right)^\prime (y) = \frac{1}{f'\left(x \right)}. \)
라이프니츠의 표기법(Leibniz's notation)을 사용하여, 위의 공식은 다음으로 쓰일 수 있습니다:
\(\quad\)\(\displaystyle \frac{dx}{dy} = \frac{1}{dy / dx}. \)
이 결과는 체인 규칙(chain rule)으로부터 따릅니다 (역 함수와 미분화(inverse functions and differentiation)에 대한 기사를 참조하십시오).
역 함수 정리는 여러 변수의 함수로 일반화될 수 있습니다. 구체적으로, 미분-가능 다변수 함수(multivariable function) \(f : \mathbf{R}^n \to \mathbf{R}^n\)는, p에서 f의 야코비 행렬(Jacobian matrix)이 역-가능(invertible)인 한, 점 p의 이웃에서 역-가능입니다. 이 경우에서, f(p)에서 \(f^{-1}\)의 야코비는 p에서 f의 야코비의 행렬 역(matrix inverse)입니다.
Real-world examples
i) f를 섭씨(Celsius)에서 화씨(Fahrenheit) 온도로 변환하는 함수로 놓습니다:
\(\quad\)\( F = f(C) = \tfrac95 C + 32 ;\)
그런-다음 그의 역 함수는 화씨를 섭씨 온도로 변환합니다:
\(\quad\)\( C = f^{-1}(F) = \tfrac59 (F - 32) ,\)
왜냐하면
\(\quad\)\(
\begin{align}
f^{-1} (f(C)) = {} & f^{-1}\left( \tfrac95 C + 32 \right) = \tfrac59 \left( (\tfrac95 C + 32 ) - 32 \right) = C, \\
& \text{for every value of } C, \text{ and } \\[6pt]
f\left(f^{-1}(F)\right) = {} & f\left(\tfrac59 (F - 32)\right) = \tfrac95 \left(\tfrac59 (F - 32)\right) + 32 = F, \\
& \text{for every value of } F.
\end{align}
\)
ii) f는 가족에서 각 아이를 그의 태어난 년도로 할당하는 것으로 가정합니다. 역 함수는 아이가 주어진 년도에서 태어난 것임을 출력할 것입니다. 어쨌든, 만약 아이들이 같은 년도에 태어났으면 (예를 들어, 쌍둥이 또는 세 쌍둥이, 등.), 출력은 입력이 공통 출생 년도일 때 절대 알려질 수 없습니다. 마찬가지로, 만약 한 년도가 아이가 태어난 적이 없는 것으로 주어지면, 아이는 지명되지 못할 것입니다. 그러나 만약 각 아이가 개별적인 년도에 태어났으면, 및 만약 우리가 아이가 태어난 삼 년에 관심을 제한하면, 우리는 역 함수를 가집니다. 예를 들어,
\(\quad\)\(\begin{align}
f(\text{Allan})&=2005 , \quad & f(\text{Brad})&=2007 , \quad & f(\text{Cary})&=2001 \\
f^{-1}(2005)&=\text{Allan} , \quad & f^{-1}(2007)&=\text{Brad} , \quad & f^{-1}(2001)&=\text{Cary}
\end{align}
\)
iii) R를 어떤 양의 x 퍼센트 상승으로 이어지는 함수로 놓고, F를 x 퍼센트 하락을 생성하는 함수로 놓습니다. x = 10%를 갖는 $100에 적용하면, 우리는 첫 번째 함수 다음에 두 번째 함수를 적용해함으로써 원래 값 $100이 복원하지 않으며, 이들 두 함수는 역이 아니라는, 감각적 인상에도 불구하고, 사실을 시연함으로써 알 수 있습니다.
iv) 용액의 pH를 계산하는 공식은 \(\rm pH=-\log_{10}[H+]\)입니다. 많은 경우에서 우리는 pH 측정으로부터 산의 농도를 찾아야 합니다. 역함수 \(\rm [H+]=10^{-pH}\)가 사용됩니다.
Generalizations
Partial inverses

심지어 만약 함수가 일-대-일이 아니면, 그것은 도메인을 제한함(restricting)으로써 f의 부분 역을 정의할 수 있을 것입니다. 예를 들어, 함수
\(\quad\)\(f(x) = x^2\)
는 일-대-일이 아닌데, 왜냐하면 \(x^2=(-x)^2\)이기 때문입니다. 어쨌든, 함수는, 만약 우리가 도메인 x ≥ 0으로 제한하면, 일-대-일이 되고, 이 경우에서 다음입니다:
\(\quad\)\(f^{-1}(y) = \sqrt{y} . \)
(만약 우리가 대신에 도메인 x ≤ 0으로 제한하면, 역은 y의 제곱 근의 음수입니다.) 대안적으로, 만약 우리가 다중-값(multivalued function) 함수인 역을 갖는 만족시키면, 도메인을 제한할 필요가 없습니다:
\(\quad\)\(f^{-1}(y) = \pm\sqrt{y} . \)

때때로 이 다중-값 역은 f의 완전한 역(full inverse)으로 불리고, (\(\sqrt{x}\) 및 \(-\sqrt{x}\)와 같은) 일부는 가지(branches)로 불립니다. 다중-값 함수의 가장 중요한 가지 (예를 들어, 양의 제곱근)은 주요 가지(principal branch)로 불리고, y에서 그의 값은 \(f^{-1}(y)\)의 주요 값(principal value)으로 불립니다.
실수 직선 위의 연속 함수에 대해, 한 가지는 지역 극값(local extrema)의 각 쌍 사이가 요구됩니다. 예를 들어, 지역 최댓값과 지역 최솟값을 갖는 삼차 함수(cubic function)의 역은 세 가지를 가집니다 (인접한 그림을 참조하십시오).
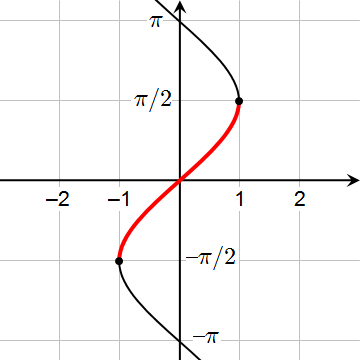
이들 고려-사항은 삼각 함수(trigonometric functions)의 역을 정의하는 것에 대해 특히 중요합니다. 예를 들어, 사인 함수(sine function)는 일대일이 아닌데 왜냐하면, 모든 각 실수 x에 대해 다음이기 때문입니다:
\(\quad\)\(\sin(x + 2\pi) = \sin(x)\)
(및 보다 일반적으로 모든 각 정수(integer) n에 대해 sin(x + 2πn) = sin(x)이기 때문입니다). 어쨌든, 사인은 구간 [−π/2, π/2] 위에 일-대-일이고, 대응하는 부분 역은 아크사인(arcsine)으로 불립니다. 이것은 역 사인의 부분 가지를 고려되므로, 역 사인의 주요 값은 항상 −π/2 및 π/2 사이에 있습니다. 다음 테이블은 각 역 삼각 함수의 주요 가지를 나타냅니다:
| 함수 | 보통 주요 값의 치역 |
| \(\arcsin\) | \(-\pi/2 \le \sin^{-1}(x) \le \pi/2\) |
| \(\arccos\) | \(0 \le \cos^{-1}(x) \le \pi\) |
| \(\arctan\) | \(-\pi/2 < \tan^{-1}(x) < \pi/2\) |
| \(\rm arccot\) | \(0 < \cot^{-1}(x) < \pi\) |
| \(\rm arcsec\) | \(0 \le \sec^{-1}(x) \le \pi\) |
| \(\rm arccsc\) | \(-\pi/2 \le \csc^{-1}(x) \le \pi/2\) |
Left and right inverses
만약 f: X → Y이면, f에 대해 왼쪽 역(left inverse) (또는 f의 리트랙션(retraction))은 다음을 만족하는 함수 g: Y → X입니다:
\(\quad\)\(g \circ f = \operatorname{id}_X . \)
즉, 함수 g는 다음 규칙을 만족시킵니다:
\(\quad\)만약 \(f(x) = y\)이면, \(g(y) = x\)입니다.
따라서, g는 f의 이미지 위의 f의 역과 반드시 같지만, 이미지 안에 있지 않은 Y의 원소에 대해 임의의 값을 취할 수 있습니다. 왼쪽 역을 갖는 함수 f는 반드시 단사입니다. 고전적 수학에서, 비-빈 도메인을 갖는 모든 각 단사 함수 f는 왼쪽 역을 반드시 가집니다; 어쨌든, 이것은 구성 수학(constructive mathematics)에서 실패할 수 있을 것입니다. 예를 들어, 실수에서 두-원소 집합의 포함 {0,1} → R의 왼쪽 역은 집합 {0,1} 에 대한 실수 직선의 리트랙션(retraction)을 제공함으로써 비-분해가능성(indecomposability)을 위반합니다.
f 오른쪽 역(right inverse) (또는 f의 섹션(section))은 다음을 만족하는 함수 h: Y → X입니다:
\(\quad\)\(f \circ h = \operatorname{id}_Y . \)
즉, 함수 h는 다음 규칙을 만족시킵니다:
\(\quad\)만약 \(\displaystyle h(y) = x\)이면, \(\displaystyle f(x) = y\)입니다.
따라서, h(y)는 f 아래 y로 매핑되는 X의 원소의 임의의 것이 될 수 있습니다. 함수 f가 오른쪽 역을 가지는 것과 (비록 일반적인 그러한 역을 구성하려면 선택의 공리(axiom of choice)를 요구할지라도) 그것이 전사인 것은 필요충분 조건입니다.
왼쪽 및 오른쪽 역 둘 다가 있는 역은 반드시 유일해야 합니다. 어쨌든, 만약 g가 f에 대해 왼쪽 역을 가지면, g는 f에 대해 오른쪽 역을 가질 수도 있거나 그렇지 않을 수 있습니다; 그리고 만약 g가 f에 대해 오른쪽 역이면, g는 f에 대해 반드시 왼쪽 역인 것은 아닙니다. 예를 들어, f: R → [0, ∞)가, R에서 모든 x에 대해 \(f(x)=x^2\)을 만족하는, 제곱하는 맵을 표시하는 것으로 놓고, g: [0, ∞) → R는, 모든 x ≥ 0에 대해 \(g(x)=\sqrt{x}\)를 만족하는, 제곱 근 맵을 표시하는 것으로 놓습니다. 그런-다음 [0, ∞)에서 모든 x에 대해 f(g(x)) = x입니다; 즉, g는 f의 오른쪽 역입니다. 어쨌든, g는 f의 왼쪽 역은 아닌데, 왜냐하면 예를 들어, g(f(−1)) = 1 ≠ −1이기 때문입니다.
Preimages
만약 f: X → Y가 임의의 함수이면 (반드시 역-가능인 것은 아닙니다), 원소 y ∈ Y의 이전-이미지(preimage) (또는 역 이미지(inverse image))는 y로 매핑되는 X의 모든 원소의 집합입니다:
\(\quad\)\(f^{-1}(\{y\}) = \left\{ x\in X : f(x) = y \right\} . \)
y의 이전-이미지는 함수 f의 (다중-값) 완전한 역 아래에서 y의 이미지(image)로 생각될 수 있습니다.
마찬가지로, 만약 S가 Y의 부분-집합(subset)이면, S의 이전-이미지는 S로 매핑되는 X의 모든 원소의 집합입니다:
\(\quad\)\(f^{-1}(S) = \left\{ x\in X : f(x) \in S \right\} . \)
예를 들어, 함수 f: R → R를 생각하는데, 여기서 \(f : x \mapsto x^2\)입니다. 이 함수는 위에 논의된 이유에 대해 역-가능이 아닙니다. 여전히 이전-이미지는 코도메인의 부분집합에 대해 정의될 수 있을 것입니다:
\(\quad\)\(f^{-1}(\left\{1,4,9,16\right\}) = \left\{-4,-3,-2,-1,1,2,3,4\right\}\)
단일 원소 y ∈ Y – 한원소 집합(singleton set) {y} – 의 이전-이미지는 때때로 y의 올(fiber)로 불립니다. Y가 실수의 집합일 때, 그것은 수준 집합(level set)으로 f −1({y})를 참조하는 것이 공통적입니다.
Further reading
- Amazigo, John C.; Rubenfeld, Lester A. (1980). "Implicit Functions; Jacobians; Inverse Functions". Advanced Calculus and its Applications to the Engineering and Physical Sciences. New York: Wiley. pp. 103–120. ISBN 0-471-04934-4.
- Binmore, K. G. (1983). "Inverse Functions". Calculus. New York: Cambridge University Press. pp. 161–197. ISBN 0-521-28952-1.
- Spivak, Michael (1994). Calculus (3th ed.). Publish or Perish. ISBN 0-914098-89-6.
- Stewart, James (2002). Calculus (5th ed.). Brooks Cole. ISBN 978-0-534-39339-7.
External links
- "Inverse function", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
- Wolfram Mathworld: Inverse Function



