수학(mathematics)에서, 기하 평균(geometric mean)은 평균(mean 또는 average)이며, 이것은 (그들의 합을 사용하는 산술 평균(arithmetic mean)과 대조적으로) 그들 값의 곱을 사용함으로써 숫자의 집합의 중심 경향 또는 전형적인 값을 가리킵니다. 기하 평균은 n 숫자의 곱(product)의 n번째 제곱근(nth root)으로 정의되며, 즉, 숫자 \(x_1, x_2, \cdots, x_n\)의 집합에 대해 기하 평균은 다음으로 정의됩니다:
\(\quad\)\(\displaystyle \left(\prod_{i=1}^n x_i\right)^\frac{1}{n} = \sqrt[n]{x_1 x_2 \cdots x_n}\)
예를 들어, 두 숫자, 말하자면 2와 8의 기하 평균은, 바로 그들 곱의 제곱근(square root), 즉, \(\sqrt{2\cdot 8}=4\)입니다. 또 다른 예제는, 세 개의 숫자 4, 1, 및 1/32의 기하 평균은 그들 곱 (1/8)의 세제곱근(cube root)이며, 이것은 1/2, 즉, \(\sqrt[3]{4\cdot 1\cdot 1/32}=1/2\)입니다.
기하 평균은 다른 항목을 비교할 때—이들 항목에 대해 단일 "성능의 지수"를 찾는 것–각 항목이 다른 수치적 범위를 가지는 여러 속성을 가질 때 종종 사용됩니다. 예를 들어, 기하 평균은 그들의 환경적 지속-가능성(environmental sustainability)에 대해 0에서 5까지 각 등급이 매겨지고, 그들의 재무건전성(financial viability)에 대해 0에서 100까지 등급이 매겨지는 두 회사를 비교하기 위해 의미있는 값을 제공할 수 있습니다. 만약 산술 평균이 기하 평균 대신에 사용되면, 재무건전성은 더 큰 가중(weight)을 가져야 하는데 왜냐하면 그의 수치적 범위가 더 크기 때문입니다. 즉, 재무 등급에서 작은 백분율 변화 (예를 들어, 80에서 90으로 진행)는 환경적 지속-가능성의 더 큰 백분율 변화 (예를 들어, 2에서 5로 진행)보다 산술 평균에서 훨씬 더 큰 차이를 만듭니다. 기하 평균의 사용은 다르게-범위진 값을 정규화(normalizes)하며, 속성의 어떤 것에서 주어진 백분율 변화가 기하 평균에 대한 같은 효과를 가짐을 의미합니다. 그래서, 4에서 4.8까지 환경적 지속-가능성에서 20% 변화는 60에서 72까지 재무건전성에서 20% 변화될 때 기하 평균에서 같은 효과를 가집니다.
기하 평균은 기하학(geometry)의 관점에서 이해될 수 있습니다. 두 숫자, \(a\)와 \(b\)의 기하 평균은, 그의 넓이가 길이 \(a\)와 \(b\)의 변을 갖는 직사각형(rectangle)의 넓이와 같은, 정사각형(square)의 한 변의 길이입니다. 비슷하게, 세 숫자 \(a\), \(b\), 및 \(c\)의 기하 평균은, 그의 부피가 그의 길이가 세 주어진 숫자와 같은 변을 갖는 직육면체(cuboid)의 부피와 같은 정육면체(cube)의 한 변의 길이입니다.
기하 평균은 오직 양의 숫자에 적용됩니다. 그것은, 세계 인구(human population)의 증가 또는 금융 투자의 이자율에 대한 데이터와 같은, 그의 값이 함께 곱해지는 것을 의미하는 것 또는 본질에서 기하적인 숫자의 집합에 대해 역시 종종 사용됩니다.
기하 평균은, 앞서 말한 산술 평균 및 조화 평균(harmonic mean)과 함께, 세 개의 고전적인 피타고라스 평균(Pythagorean means)의 역시 하나입니다. 적어도 하나의 같지-않은 값을 포함하는 모든 양의 데이터 집합에 대해, 조화 평균은 세 평균 중에 항상 가장 작은 값이지만, 산술 평균은 세 값 중에 항상 가장 큰 것이고 기하 평균은 항상 그 사이에 있습니다 (산술 및 기하 평균의 부등식을 참조하십시오).
Calculation
데이터 집합 \(\left\{a_1, a_2,\, \ldots,\, a_n\right\}\)의 기하 평균은 다음에 의해 제공됩니다:
\(\quad\)\(\displaystyle \left(\prod_{i=1}^n a_i \right)^\frac{1}{n} = \sqrt[n]{a_1 a_2 \cdots a_n}.\)
위 수식은 곱셈의 급수를 보이기 위해 대문자 파이 표기법(capital pi notation)을 사용합니다. 등호의 각 변은 값의 집합이 그 값의 전체 곱(product)을 제공하기 위해 (값의 숫자는 "n"에 의해 표시됩니다) 연속적으로 곱해지고, 그런-다음 전체 곱의 n번째 근은 원래 집합의 기하 평균을 제공하기 위해 취해집니다. 예를 들어, 네 숫자 \(\{1, 2, 3, 4\}\)의 집합에서, \(1 \times 2 \times 3 \times 4\)의 곱은 \(24\)이고, 기하 평균은 24의 네 번째 근, 또는 ~ 2.213입니다. 왼쪽 변의 지수 \(\frac{1}{n}\)은 n번째 근을 취하는 것과 동등합니다. 예를 들어, \(24^\frac{1}{4} = \sqrt[4]{24}\)입니다.
데이터 집합의 기하 평균은 만약 모든 구성원이 같지 않으면 데이터 집합의 산술 평균보다 작으며, 이 경우에서 기하 및 산술 평균(arithmetic mean)은 같습니다. 이것은 산술-기하 평균(arithmetic-geometric mean)의 정의를 허용하며, 둘 사이의 교차는 항상 사이에 있습니다.
기하 평균은 역시 만약 두 수열(sequence) (\(a_n\)) 및 (\(h_n\))가 다음과 같이 정의되면, 그런 의미에서 산술-조화 평균입니다:
\(\quad\)\(\displaystyle a_{n+1} = \frac{a_n + h_n}{2}, \quad a_0 = x\)
및
\(\quad\)\(\displaystyle h_{n+1} = \frac{2}{\frac{1}{a_n} + \frac{1}{h_n}}, \quad h_0 = y\)
여기서 \(h_{n+1}\)는 두 수열의 이전 값의 조화 평균(harmonic mean)이며, 그런-다음 \(a_n\) 및 \(h_n\)는 \(x\) 및 \(y\)의 기하 평균으로 수렴할 것입니다.
이것은 수열이 공통 극한 (이것은 볼차노–바이어슈트라스 정리(Bolzano–Weierstrass theorem)에 의해 표시될 수 있음)으로 수렴한다는 사실과 기하학적 평균이 보존된다는 사실에서 쉽게 알 수 있습니다:
\(\quad\)\(\displaystyle \sqrt{a_i h_i} =
\sqrt{\frac{a_i + h_i}{\frac{a_i + h_i}{h_i a_i}}} =
\sqrt{\frac{a_i + h_i}{\frac{1}{a_i} + \frac{1}{h_i}}} =
\sqrt{a_{i+1} h_{i+1}}\)
반대, 유한 지수의 일반화된 평균(generalized mean)의 쌍에 의한 산술 및 조화 평균을 대체하면 같은 결과를 산출합니다.
Relationship with logarithms
기하 평균은 로그의 산술 평균의 지수로 역시 표현될 수 있습니다. 공식을 변환하기 위해 로그 항등식(logarithmic identities)을 사용함으로써, 곱셈은 합으로 표현될 수 있고 곱셈으로 거듭제곱을 표현할 수 있습니다:
\(a_1, a_2, \dots, a_n > 0\)일 때:
\(\quad\)\(\displaystyle \left( \prod_{i=1}^n a_i \right)^\frac{1}{n} = \exp\left[\frac{1}{n} \sum_{i=1}^n \ln a_i\right];\)
추가적으로, 만약 \(a_i\)의 음의 값이 허용되면,
\(\quad\)\(\displaystyle \left( \prod_{i=1}^n a_i \right)^\frac{1}{n} = \left(\left(-1\right)^m\right)^\frac{1}{n} \exp\left[\frac{1}{n}\sum_{i=1}^n \ln \left|a_i\right| \right],\)
여기서 m은 음수의 숫자입니다.
이것은 로그-평균으로 때때로 불립니다 ((같은 이름의) 로그 평균(logarithmic average)과 혼동해서는 안됩니다). 단순히 \(a_i\)의 로그-변환된 값의 산술 평균(arithmetic mean) (즉, 로그 스케일에 대한 산술 평균)을 계산하고 그런-다음 원래 스케일로 계산을 반환하기 위해 지수화를 사용합니다, 즉, \(f(x) = \log x\)를 갖는 일반화된 f-평균(generalised f-mean)입니다. 예를 들어, 2와 8의 기하 평균은 다음으로 계산될 수 있으며, 여기서 \(b\)는 로그(logarithm)의 임의의 밑수 (공통적으로 2, \(e\) 또는 10)입니다:
\(\quad\)\(\displaystyle b^{\frac{1}{2}\left[\log_b (2) + \log_b (8)\right]} = 4\)
위와 관련하여, 점 \(a_1, \ldots, a_n\)의 주어진 표본에 대해, 기하 평균은 \(\displaystyle f(a) = \sum_{i=1}^n (\log(a_i) - \log(a))^2\)의 최소기이지만, 반면에 산술 평균은 \(\displaystyle f(a) = \sum_{i=1}^n (a_i - a)^2\)의 최소기임을 알 수 있습니다. 따라서, 기하 평균은 그의 지수가 (최소 제곱의 의미에서) 표본의 지수와 가장 일치하는 표본의 요약을 제공합니다.
기하 평균의 로그 형식은 일반적으로 컴퓨터 언어로 구현에 대해 선호되는 대안인데 왜냐하면 많은 숫자의 곱을 계산하면 산술 오버플로(arithmetic overflow) 또는 산술 언더플로(arithmetic underflow)가 이어질 수 있기 때문입니다. 이것은 각 숫자에 대해 로그의 합으로 발생할 가능성이 적습니다.
Comparison to arithmetic mean
(양의) 숫자의 비-빈 데이터 집합의 기하 평균은 항상 최대 그들의 산술 평균입니다. 상등은 데이터 집합에서 모든 숫자가 같을 때 오직 얻어집니다; 그렇지 않으면, 기하 평균이 더 작습니다. 예를 들어, 242와 288의 기하 평균은 264와 같지만, 그들의 산술 평균은 265입니다. 특히, 이것은 비-동일한 숫자의 집합이 평균-보존하는 확산(mean-preserving spread)에 영향을 받을 때 — 즉, 집합의 원소는 산술 평균을 변경하지 않은 채로 서로로부터 보다 "별개로 확산"됩니다 — 그들의 기하학적 평균이 감소한다는 것을 의미합니다.
Average growth rate
많은 경우에서, 기하 평균은 일부 양의 평균 성장률을 결정하기 위한 가장-좋은 측정입니다. (예를 들어, 만약 1년 동안 매출이 80%, 내년에 25% 증가하면, 최종 결과는 50%의 상수 성장률의 그것과 같은데, 왜냐하면 1.80과 1.25의 기하 평균은 1.50이기 때문입니다.) 평균 성장률을 결정하기 위해, 모든 단계에서 측정된 성장률의 곱을 취할 필요는 없습니다. 양을 수열 \(a_0, a_1,..., a_n\)으로 제공된 것으로 놓으며, 여기서 \(n\)은 초기 상태에서 최종 상태까지의 단계의 숫자입니다. 연속 측정 \(a_k\) 및 \(a_{k+1}\) 사이의 성장률은 \(a_{k+1}/a_k\)입니다. 이들 성장률의 기하 평균은 그런-다음 바로 다음입니다:
\(\quad\)\(\left(\displaystyle \frac{a_1}{a_0} \frac{a_2}{a_1} \cdots \frac{a_n}{a_{n-1}} \right)^\frac{1}{n} = \left(\frac{a_n}{a_0}\right)^\frac{1}{n}.\)
Application to normalized values
임의의 다른 평균에 대해 유지되지 않는 기하 평균의 기본 속성은 같은 길이의 두 수열 \(X\) 및 \(Y\)에 대해, 다음입니다:
\(\quad\)\(\displaystyle \operatorname{GM}\left(\frac{X_i}{Y_i}\right) = \frac{\operatorname{GM}(X_i)}{\operatorname{GM}(Y_i)}\)
이것은 정규화된 결과를 평균할 때 기하 평균을 유일한 올바른 평균으로 만듭니다; 즉, 참조 값에 대한 비율로 표시되는 결과입니다. 이것은 참조 컴퓨터와 관한 컴퓨터 성능을 제시할 때, 또는 여러 이기종 원천 (예를 들어, 기대 수명, 교육 기간, 및 유아 사망률)로부터 단일 평균 지수를 계산할 때 경우입니다. 이 시나리오에서, 산술 또는 조화 평균을 사용하면 참조로 사용되는 것에 따라 결과 순위가 변경되어야 합니다. 예를 들어, 컴퓨터 프로그램의 실행 시간의 다음 비교를 취합니다:
| 컴퓨터 A | 컴퓨터 B | 컴퓨터 C | |
| 프로그램 1 | 1 | 10 | 20 |
| 프로그램 2 | 1000 | 100 | 20 |
| 산술 평균 | 500.5 | 55 | 20 |
| 기하 평균 | 31.622... | 31.622... | 20 |
| 조화 평균 | 1.998... | 18.182... | 20 |
산술 및 기하 평균은 컴퓨터 C가 가장 빠르다는 것에 "동의함"을 의미합니다. 어쨌든, 적절하게 정규화된 값을 제시하고 산술 평균을 사용함으로써, 우리는 다른 두 컴퓨터 중 하나가 가장 빠르다는 것을 알 수 있습니다. A의 결과로 정규화하면 산술 평균에 따라 가장 빠른 컴퓨터로 A를 제공합니다:
| 컴퓨터 A | 컴퓨터 B | 컴퓨터 C | |
| 프로그램 1 | 1 | 10 | 20 |
| 프로그램 2 | 1 | 0.1 | 0.02 |
| 산술 평균 | 1 | 5.05 | 10.01 |
| 기하 평균 | 1 | 1 | 0.632... |
| 조화 평균 | 1 | 1.198... | 0.039... |
반면에 B의 결과로 정규화하면 산술 평균에 따라 가장 빠른 컴퓨터로 B를 제공하지만 조화 평균에 따라 가장 빠른 컴퓨터로 A를 제공합니다:
| 컴퓨터 A | 컴퓨터 B | 컴퓨터 C | |
| 프로그램 1 | 0.1 | 1 | 2 |
| 프로그램 2 | 10 | 1 | 0.2 |
| 산술 평균 | 5.05 | 1 | 1.1 |
| 기하 평균 | 1 | 1 | 0.632 |
| 조화 평균 | 0.198... | 1 | 0.363... |
그리고 C의 결과로 정규화하면 산술 평균에 따라 가장 빠른 컴퓨터로 C를 제공하지만 조화 평균에 따라 가장 빠른 컴퓨터로 A를 제공합니다:
| 컴퓨터 A | 컴퓨터 B | 컴퓨터 C | |
| 프로그램 1 | 0.05 | 0.5 | 1 |
| 프로그램 2 | 50 | 5 | 1 |
| 산술 평균 | 25.025 | 2.75 | 1 |
| 기하 평균 | 1.581... | 1.581... | 1 |
| 조화 평균 | 0.999... | 0.909... | 1 |
모든 경우에서, 기하 평균으로 제공되는 순위는 정규화되지 않은 값으로 얻은 순위와 같게 유지됩니다.
어쨌든, 이 추론은 문제가 제기되어져 왔습니다. 일관된 결과를 제공하는 것이 항상 올바른 결과를 제공하는 것과 같지는 않습니다. 일반적으로, 프로그램의 각각에 가중을 할당하고, (산술 평균을 사용하여) 평균 가중된 실행 시간을 계산하고, 그런-다음 해당 결과를 컴퓨터 중 하나에 정규화하는 것이 더 엄격합니다. 위의 세 테이블은 프로그램의 각각에 다른 가중을 단지 부여하며, 산술 및 조화 평균의 일관되지 않은 결과를 설명합니다 (첫 번째 테이블은 두 프로그램 모두에 같은 가중을 부여하고, 두 번째는 두 번째 프로그램에 1/1000의 가중을 부여하고, 세 번째는 두 번째 프로그램에 1/100, 첫 번째 프로그램에 1/10의 가중을 부여합니다.) 산술 평균에서처럼 더해지는 회수와 달리, 실행 횟수를 곱하면 물리적 의미가 없기 때문에, 가능하면 성능 수치를 집계하기 위한 기하 평균의 사용은 피해져야 합니다. 시간에 반비례하는 메트릭 (속도-향상, IPC)은 조화 평균을 사용하여 평균화해야 합니다.
기하 평균은 \(p\)가 영으로 갈 때 그것의 극한으로 일반화된 평균(generalized mean)에서 도출될 수 있습니다. 비슷하게, 이것은 가중된 기하 평균에 대해서도 가능합니다.
Applications
Proportional growth
기하 평균은 비례적 성장, 지수적 성장(exponential growth) (상수 비례적 성장) 및 다양한 성장 둘 다를 설명하는 산술 평균(arithmetic mean)보다 더 적합합니다; 영업에서 성장률의 기하 평균은 복리 연간 성장률(compound annual growth rate) (CAGR)로 알려져 있습니다. 기간에 걸쳐 성장의 기하 평균은 같은 최종 양을 산출하려고 하는 동등한 상수 성장률을 산출합니다.
오렌지 나무가 1년에 100 오렌지를 산출하고 그런-다음 따라오는 해에 180, 210 및 300을 생산한다고 가정하면, 따라서 성장은 각각 매년마다 80%, 16.6666% 및 42.8571%입니다. 산술 평균(arithmetic mean)을 사용하는 것은 46.5079% (80% + 16.6666% + 42.8571%, 그 합계를 3으로 나눈 값)의 (선형) 평균 성장을 계산합니다. 어쨌든, 만약 우리가 100 오렌지로 시작하고 그것을 매년 46.5079%의 성장하는 것으로 놓으면, 그 결과는 300이 아닌 314 오렌지가 되므로, 선형 평균은 전년 대비 성장을 초과합니다.
대신에, 우리는 기하학적 평균을 사용할 수 있습니다. 80%로 증가하면 1.80을 곱한 값에 해당하므로, 우리는 1.80, 1.166666 및 1.428571의 기하 평균, 즉 \(\sqrt[3]{1.80 \times 1.166666 \times 1.428571} \approx 1.442249\)를 취합니다; 따라서 연간 "평균" 성장은 44.2249%입니다. 만약 우리가 100 오렌지로 시작하고 매년 44.2249%로 숫자를 늘리면, 그 결과는 300 오렌지입니다.
Financial
기하 평균은 재무 지수를 계산하기 위해 때때로 사용되어져 왔습니다 (평균화 하는 것은 지수의 성분 위에 있습니다). 예를 들어 과거에는 FT 30 지수가 기하 평균을 사용했습니다. 역시 영국과 유럽 연합에서 최근 도입된 인플레이션의 "RPIJ" 측정에서 사용됩니다.
이것은 산술 평균을 사용하는 것과 비교하여 지수에서 움직임을 과소-평가하는 효과를 가집니다.
Applications in the social sciences
비록 기하 평균은 사회적 통계량 계산에서 상대적으로 드물었지만, 2010년부터 시작하여 유엔 인간 개발 지수는 다음과 같이 수집되고 비교되는 통계량의 대체할 수 없는 본성을 더 잘 반영한다는 배경 위에, 계산의 이 모드로 전환했습니다.
- 기하 평균은 [비교되는] 차원들 사이의 대체-가능성의 수준을 감소시키고 동시에 출생시 말하자면 기대 수명의 1% 감소가 교육 또는 소득에서 1% 감소와 같은 HDI에 같은 영향을 미치는 것을 보장합니다. 따라서, 성과 비교를 위한 기초로, 이 방법은 단순한 평균보다 차원에 걸쳐 본질적인 차이를 더 존중합니다.
HDI (인간 개발 지수)를 계산하는 데 사용된 모든 값이 정규화된 것은 아닙니다; 그중 일부는 대신에 형식 \(\left(X - X_\text{min}\right) / \left(X_\text{norm} - X_\text{min}\right)\)을 가집니다. 이것은 기하 평균의 선택을 위의 "속성" 섹션에서 기대하는 것보다 덜 분명하게 만듭니다.
1.0의 불평등 회피 매개변수를 갖는 앳킨슨 지수(Atkinson Index)와 결합된 같게 분포된 복지 동등한 소득은 단순히 소득의 기하 평균입니다. 일 이외의 값에 대해, 동등한 값은 Lp 노름(Lp norm)을 원소의 숫자로 나눈 값이며, p는 일에서 부등식 혐오 매개-변수를 뺀 값과 같습니다.
Geometry
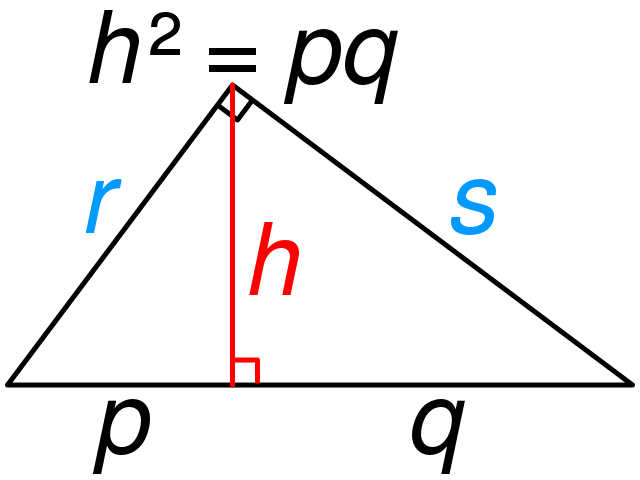
직각 삼각형(right triangle)의 경우에서, 그것의 고도는 빗변에서 90° 꼭짓점까지 수직으로 연장되는 선분의 길이입니다. 이 선분이 빗변을 두 선분으로 나눈다고 생각하면, 이들 선분 길이의 기하 평균은 고도의 길이입니다. 이 속성은 기하 평균 정리(geometric mean theorem)로 알려져 있습니다.
타원(ellipse)에서, 반-보조 축(semi-minor axis)은 초점(focus)으로부터 타원의 최대 및 최소 거리의 기하 평균입니다; 그것은 역시 반-주요 축(semi-major axis)과 반-래투스 렉텀(semi-latus rectum)의 기하 평균입니다. 타원의 반-주요 축(semi-major axis)은 중심에서 한 초점까지의 거리와 중심에서 한 방향선(directrix)까지의 거리의 기하 평균입니다.
구(sphere)의 수평선(horizon)까지의 거리는 구의 가장 가까운 점까지의 거리가 작을 때 구의 가장 가까운 점까지의 거리와 구의 가장 먼 점까지의 거리의 기하 평균과 근사적으로 같습니다.
라마누젠 (1914)에 따른 원을 정사각형의 근사에서 및 "sent by T. P. Stowell, credited to Leybourn's Math. Repository, 1818"에 따른 십칠각형(Heptadecagon)의 구성 둘 다에서, 기하 평균이 사용됩니다.
Aspect ratios
기하 평균은 영화와 비디오에서 타협 가로-세로 비율(aspect ratio)을 선택하는 것에서 사용되어져 왔습니다: 두 가로-세로 비율이 주어지면, 그들의 기하 평균은 둘 사이의 타협을 제공하며, 균일하게 어떤 의미에서 둘 다 왜곡되거나 잘립니다. 구체적으로, 다른 가로-세로 비율의 두 같은 넓이 (같은 중심과 평행 변을 갖는) 직사각형은 그들의 가로-세로 비율이 기하 평균인 직사각형에서 교차하고, 마찬가지로 (그들의 둘 다를 포함하는 가장 작은 직사각형) 덮개는 그들의 기하 평균의 가로-세로 비율을 가집니다.
SMPTE에 의한 16:9 가로-세로 비율의 선택에서, 2.35와 4:3의 균형을 맞추면, 기하 평균은 2\(\sqrt{2.35 \times \frac{4}{3}} \approx 1.7701\)이고, 따라서 \(16:9 = 1.77\overline{7}\)...가 선택됩니다. 이것은 컨스 파워스(Kerns Powers)에 의해 경험적으로 발견되었으며, 그는 같은 넓이를 갖는 사각형을 잘라내고 각각의 인기있는 가로-세로 비율에 맞게 사각형을 형성했습니다. 중심 점을 정렬한 상태에서 겹칠 때, 그는 그들의 가로-세로 비율 사각형의 모두는 1.77:1의 가로-세로 비율를 갖는 외부 직사각형 이내에 맞추고, 그들의 모두는 같은 가로-세로 비율 1.77:1을 갖는 더 작은 공통 내부 직사각형을 역시 덮었습니다. 파워스에 의해 발견된 값은 극단 가로-세로 비율, 4:3 (1.33:1) 및 시네마스코프(CinemaScope) (2.35:1)의 기하 평균이며, 시네마스코프는 우연히 \(16:9\) (\(1.77\overline{7}:1\))에 가깝습니다. 중간 비율은 결과, 오직 두 극단 비율에 영향을 미치지 않습니다.
같은 기하 평균 기법을 16:9 및 4:3에 적용하면 근사적으로 14:9 (\(1.55\overline{5}\)...) 가로-세로 비율을 산출하며, 이것은 이들 비율 사이의 타협으로 마찬가지로 사용됩니다. 이 경우에서 14:9는 정확히 \(16:9\) 및 \(4:3 = 12:9\)의 산술 평균(arithmetic mean)인데, 왜냐하면 14는 16과 12의 평균이지만, 정확한 기하 평균은 \(\sqrt{\frac{16}{9}\times\frac{4}{3}} \approx 1.5396 \approx 13.8:9\)이기 때문이며, 그러나 두 다른 평균, 산술과 기하는 근사적으로 같은데 왜냐하면 두 숫자가 서로 충분히 가깝기 때문입니다 (2% 미만의 차이가 있습니다).
Spectral flatness
신호 처리(signal processing)에서, 스펙트럼이 얼마나 평탄 또는 뾰족한지의 측정, 스펙트럼 평탄도(spectral flatness)는 파워 스펙트럼의 기하 평균과 그것의 산술 평균의 비율로 정의됩니다.
Anti-reflective coatings
광학 코팅에서, 여기서 반사는 굴절률 \(n_0\)와 \(n_2\)의 두 미디어 사이의 최소화해야 하며, 역-반사 코팅(anti-reflective coating)의 최적 굴절률 \(n_1\)은 기하 평균: \(n_1 = \sqrt{n_0 n_2}\)에 의해 제공됩니다.
Subtractive color mixing
(같은 색조(tinting) 강도, 불투명도(opacity) 및 희석률(dilution)의) 페인트 혼합(mixtures)에 대해 스펙트럼 반사율 곡선(spectral reflectance curve)은 그들의 스펙트럼(spectra)의 각 파장에서 계산된 페인트의 개별 반사율 곡선의 기하 평균입니다.
Image Processing
기하 평균 필터(geometric mean filter)는 이미지 처리(image processing)에서 노이즈 필터로 사용됩니다.
External links
- Calculation of the geometric mean of two numbers in comparison to the arithmetic solution
- Arithmetic and geometric means
- When to use the geometric mean
- Practical solutions for calculating geometric mean with different kinds of data
- Geometric Mean on MathWorld
- Geometric Meaning of the Geometric Mean
- Geometric Mean Calculator for larger data sets
- Computing Congressional apportionment using Geometric Mean
- Non-Newtonian calculus website
- Geometric Mean Definition and Formula
