이차 함수(quadratic function)는 다항함수 중에서 최고차항이 2차인 함수입니다.
이차 함수는 정의역과 공역이 실수의 집합인, 다음과 같은 꼴의 함수입니다.
\(\quad\)\(f(x)=ax^2+bx+c\,(a\neq 0)\)
여기서 \(a\,(a\neq 0),\, b,\,c\)는 임의의 실수입니다.
일반적으로 새로운 함수를 만났을 때에는 정의역을 파악하는 것이 중요합니다. 정의역은 함수의 특징을 파악하기 위해서 대입해 볼 수 있는 것들을 의미합니다. 정의역에 없는 것은 대입을 해서는 안됩니다.
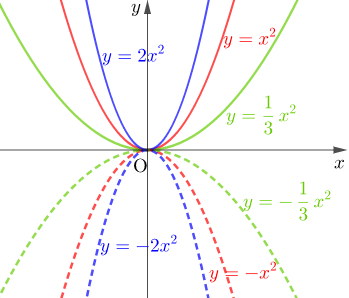
이전 과정에서 일차함수를 배울 때에도 가장 기본 모양에 정수를 하나씩 대입해서 그 결과를 이어서 직선의 모양을 갖는 것을 알아내었습니다. 지금도 마찬가지입니다. 이차함수의 가장 기본 모양에 정수를 하나씩 대입해서 좌표평면에 찍어보면 오른쪽과 같은 결과를 볼 수 있습니다.
\(\quad\)\(y=ax^2\,(a\neq0)\)
이 모양을 포물선이라고 부릅니다.
우선 이전과정에서 실수의 제곱은 비-음수(\(\ge 0\))라는 사실을 알고 있습니다. 여기서 \(x^2\)이 이에 해당합니다. 그러므로 \(a\)의 부호에 따라 모양이 달라진다는 것을 알 수 있습니다.
- \(a>0\rightarrow y\geq 0\) : \(x=0\)에서 \(x\)축 (\(y=0\))과 만나고, \(x\)축 위에만 존재합니다.
- \(a<0\rightarrow y\leq 0\) : \(x=0\)에서 \(x\)축 (\(y=0\))과 만나고, \(x\)축 아래에만 존재합니다.
다음으로는 \(a\)의 크기 (\(|a|\))에 따라 모양이 어떻게 바뀌는지 확인을 해야 합니다. 일반적으로 곱해지는 숫자는 1을 기준으로 하는 경우가 많습니다.
- \(|a|>1\)인 경우는 값이 클수록 급격히 모양이 변해서 폭이 좁아집니다.
- \(|a|<1\)인 경우는 값이 작을수록 완만히 모양이 변해서 폭이 넓어집니다.
이차함의 계수가 중요한 이유는 이차항의 계수의 절댓값이 같아야만 평행이동이나 대칭이동을 통해서 서로 겹칠 수 있기 때문입니다. 두 이차함수 사이의 넓이 등을 구할 때, 적분을 사용하지 않고 구하기 위해서는, 이동이 되는 경우밖에 없으므로 이차항의 계수가 같아야 합니다.
꼭짓점
중요한 특징에는 그에 맞는 이름을 만들게 됩니다. 이차함수에서는 제일 중요한 점이 \((0,0)\)입니다. 왜냐하면, 이 점을 기점으로 증감이 변하게 되기 때문입니다.
예를 들어 \(a>0\)일 때 다음과 같이 증감이 변합니다.
- \(x\geq0\)에서 증가(\(x_1>x_2\rightarrow f(x_1)>f(x_2)\))합니다.
- \(x\leq0\)에서 감소(\(x_1>x_2\rightarrow f(x_1)<f(x_2)\))합니다.
이런 연유로 이점을 포물선의 꼭짓점이라고 합니다.
대칭축
이차함수 \(y=ax^2\,(a\neq0)\)의 모양은 \(y\)축 (\(x=0\))에 대해서 대칭입니다. 이 축을 대칭축이라고 합니다.
대칭축은 꼭짓점의 \(x\)좌표를 구성합니다. 이차함수는 한 좌표를 알면, 다른 좌표는 대입해서 구할 수 있기 때문에 대칭축을 알고 있다면, 꼭짓점도 구할 수 있다는 것을 의미합니다. 이런 이유로 대칭축을 알고 있는 것이 보다 유리합니다.
이차함수의 평행이동
함수의 평행이동은 해당 함수가 가진 특징을 그대로 유지하면서 다른 곳으로 이동시키는 역할을 합니다. 예를 들어, \(y=2x^2\)을 \(x\)축으로 3만큼 \(y\)축으로 5만큼 평행이동한 식은 아래와 같습니다.
\(\quad\)\(y-5=2(x-3)^2\)
이 함수의 특징은 다음과 같습니다. 이동 전 함수의 특징과 비교해 보는 것이 좋겠습니다.
| 함수 | 꼭짓점 | 대칭축 |
| \(y=2x^2\) | \((0,0)\) | \(x=0\) |
| \(y-5=2(x-3)^2\) | \((3,5)\) | \(x=3\) |
이차함수의 표준형
이차함수의 표준형은 이차함수의 특징이 잘 나타나도록 식이 만들어진 것을 선택합니다. 이후에 다른 함수들도 표준형은 함수의 특징을 잘 나타내도록 만들어진 식을 말합니다.
\(\quad\)\(y=a(x-p)^2+q\)
여기서 꼭짓점은 \((p,q)\)이며, 대칭축은 \(x=p\)입니다. 만들어진 모양에서 바로 확인이 됩니다.
이차함수의 일반형
일반형이라고 알려진 식이 정의식이며, 위에 소개된 표준형을 전개해서 정리한 식이 일반형입니다.
함수의 특징을 알아보기 위해서 일반형을 표준형으로 바꿀 필요가 있습니다. 이 과정을 일반식으로 유도하면 아래와 같습니다.
\(\quad\)\(\begin{align}y
&=ax^2+bx+c\,(a\neq0)\\
&=a\left(x^2+\frac{b}{a}x\right)+c\\
&=a\left(x^2+\frac{b}{a}x+\frac{b^2}{4a^2}-\frac{b^2}{4a^2}\right)+c\\
&=a\left(x+\frac b{2a}\right)^2-\frac{b^2}{4a}+c\\
&=a\left(x+\frac b{2a}\right)^2-\frac{b^2-4ac}{4a}\\
\end{align}\)
이 식으로부터 꼭짓점 \(\displaystyle \left(-\frac b{2a}, \frac{b^2-4ac}{4a}\right)\)이며, 대칭축은 \(\displaystyle x=-\frac b{2a}\)입니다.
그러나 모든 것을 암기해서 풀기는 어렵습니다. 또한 식이 복잡해질수록 실수가 많아집니다.
다른 접근
만약 암기가 필요하다면, 대칭축을 외우는 것이 유리합니다. 꼭짓점의 \(x\)좌표는 대칭축이며, \(y\)좌표는 주어진 식에 대입해서 구할 수 있기 때문입니다.
그럼 실제 문제에서 일반식을 표준형으로 어떻게 바꾸는 게 좋은가요? 아래의 과정을 통해 알아보겠습니다.
\(\quad\)\(\begin{align}
y & = 2x^2-12x+23 \\
& = 2\left(x^2-6x\right)+\cdots \\
& = 2\left(x-3\right)^2+\cdots \\
\end{align}\)
이 과정에서, 선행 계수로 묶어내는 부분에서 실수를 하는 경우가 꽤 많습니다. 실제 계산에서, 역과정, 즉 전개를 통해서 원래 식이 나오는지 확인할 수 있습니다.
여기까지 구하면 다 구한 것입니다. 구해진 식으로부터 대칭축이 \(x=3\)인 것을 알 수 있습니다. 그러므로 꼭짓점의 \(x\)좌표 (독립변수)가 3이므로 주어진 원래 식에 대입해서 (종속변수인) \(y=5\)라는 결과를 알 수 있습니다. 그러므로 표준형은 아래와 같이 만들어집니다.
\(\quad\)\(y-5=2(x-3)^2\)
\(\quad\)\(\therefore y=2(x-3)^2+5\)
이런 접근은, 완전제곱식을 만들어서 구하는 것에 비해, 식이 복잡해질수록 더 위력을 발휘합니다.
응용예제
응용예제1
좌표평면에서 이차 함수 \(y=\frac{1}{k}x^2+\frac{3}{k}x+k\)의 그래프와 직선 \(y=mx+n\)의 길이는 \(k\)의 값에 관계없이 항상 일정합니다. 이때, \(\overline{AB}\)의 값을 구하시오. (단, \(k\)는 0이 아닌 실수입니다.)
응용예제2
이차함수 \(f(x)\)가 다음 조건을 만족시킵니다.
\(\quad\)(가) \(x\)에 대한 방정식 \(f(x)=2\)의 두 근은 1과 3입니다.
\(\quad\)(나) \(-2 \le x \le 0\)에서 이차함수 \(f(x)\)의 최댓값은 –4입니다.
\(f(2)\)의 값은?
응용예제3
이차함수 \(y=x^2-2x-3\) 위의 두 점 \(\mathrm{P}(x_1,y_1)\)과 \(\mathrm{Q}(x_2,y_2)\)가 직선 \(y=x+1\)에 대하여 대칭일 때, \(x_1^2+x_2^2\)의 값을 구하여라.
응용예제4
이차함수 \(y=x^2-2x-3\) 위의 두 점 \(\mathrm{P}(x_1,y_1)\)과 \(\mathrm{Q}(x_2,y_2)\)가 직선 \(y=x+1\)에 대하여 대칭일 때, \(x_1^2+x_2^2\)의 값을 구하여라.
응용예제5
이차방정식 \(x^2-5x+5=0\)의 두 근을 \(\alpha,\beta\)라고 할 때, 세 점 \((\alpha,\beta)\), \((\beta, \alpha)\), \((1,5)\)를 지나고 축이 \(y\)축에 평행한 이차함수의 방정식을 구하여라.
응용예제6
이차함수 \(y=x^2+bx+c\)의 꼭짓점이 \((a+2,2a-1)\)이라고 하면, 이 이차함수가 \(a\)의 값에 관계없이 일정한 곡선에 접합니다. 이 직선의 방정식을 구하여라.
응용예제7
이차함수 \(y=2x^2\) 위의 서로 다른 두 점 \(\mathrm{P,Q}\)에서의 접선이 직교합니다. 이 접선의 교점이 그리는 도형의 방정식은?
응용예제8
두 함수 \(f(x)=x^2-mx+4m\), \(g(x)=-x^2+3x+3m-3\)과 임의의 두 실수 \(x_1, x_2\)에 대하여 부등식 \(f(x_1) \ge g(x_2)\)가 성립하도록 하는 상수 \(m\)의 값의 범위는?

