삼각형의 무게 중심(center of gravity)은 삼각형의 세 꼭짓점에서 각 꼭짓점의 대변의 중점을 연결한 선분(중선)의 교점을 말합니다.

삼각형의 무게중심은 세 중선을 꼭짓점으로부터 \(2:1\)로 내분합니다. 이 특징을 이용해서 삼각형의 꼭짓점의 좌표가 주어졌을 때, 무게중심의 좌표를 구해보겠습니다.
\(\triangle\mathrm{ABC}\)의 세 꼭짓점의 좌표가
\(\quad\)\(\mathrm A(x_1,y_1), \mathrm B(x_2,y_2), \mathrm C(x_3,y_3)\)
로 주어졌을 때, 선분 \(\mathrm{BC}\)의 중점 \(\mathrm M\)은 수직선 위의 내분점에 따라 다음과 같이 구해집니다.
\(\quad\)\(\displaystyle\mathrm M\left(\frac{x_2+x_3}{2},\frac{y_2+y_3}{2}\right)\)
또한, 선분 \(\mathrm{AM}\)을 \(2:1\)로 내분하는 무게중심 \(\mathrm G\)의 좌표는 다음과 같이 구해집니다.
\(\quad\)\(\displaystyle\mathrm G\left(\frac{2\cdot\frac{x_2+x_3}{2}+x_1}{2+1},\frac{2\cdot\frac{y_2+y_3}{2}+y_1}{2+1}\right)\)
그러므로 삼각형의 무게중심 \(\mathrm G\)의 좌표는 다음과 같습니다.
\(\quad\)\(\displaystyle\mathrm G\left(\frac{x_1+x_2+x_3}{3},\frac{y_1+y_2+y_3}{3}\right)\)
기억할 만한 것

삼각형의 각 변을 같은 방향으로 같은 비율로 내분한 세 점으로 이루어지는 삼각형도 원래 삼각형의 무게중심과 동일합니다. 또한 같은 방법으로 외분한 점들로 구성된 삼각형도 원래 삼각형의 무게중심과 같습니다. 한마디로 별도로 계산할 필요가 없다는 것입니다.
예를 들어, 오른쪽 그림과 같이 \(\triangle \mathrm{ABC}\)의 각 선분을 \(1:3\)으로 내분하는 점 \(\mathrm{P,Q,R}\)로 만들어지는 \(\triangle \mathrm{PQR}\)의 무게중심은 \(\triangle \mathrm{ABC}\)의 무게중심과 동일합니다. 그러므로 \(\triangle \mathrm{PQR}\)의 무게중심을 구하기 위해서 점 \(\mathrm{P,Q,R}\)의 좌표를 구할 필요는 없습니다. 원래 주어지는 점 \(\mathrm{A,B,C}\)의 좌표로 구해도 같은 무게중심의 좌표를 나타냅니다.
응용예제
응용예제1
\(\mathrm{A}(2,2)\)이고 무게중심이 원점인 정삼각형 \(\mathrm{ABC}\)가 있습니다. 다음을 구하시오.
\(\quad\)(ㄱ) 정삼각형의 한 변의 길이
\(\quad\)(ㄴ) 꼭짓점 \(\mathrm{B,C}\)의 좌표를 구하여라. (단 점 \(\mathrm{B}\)의 \(x\)-좌표는 음수입니다.)
응용예제2
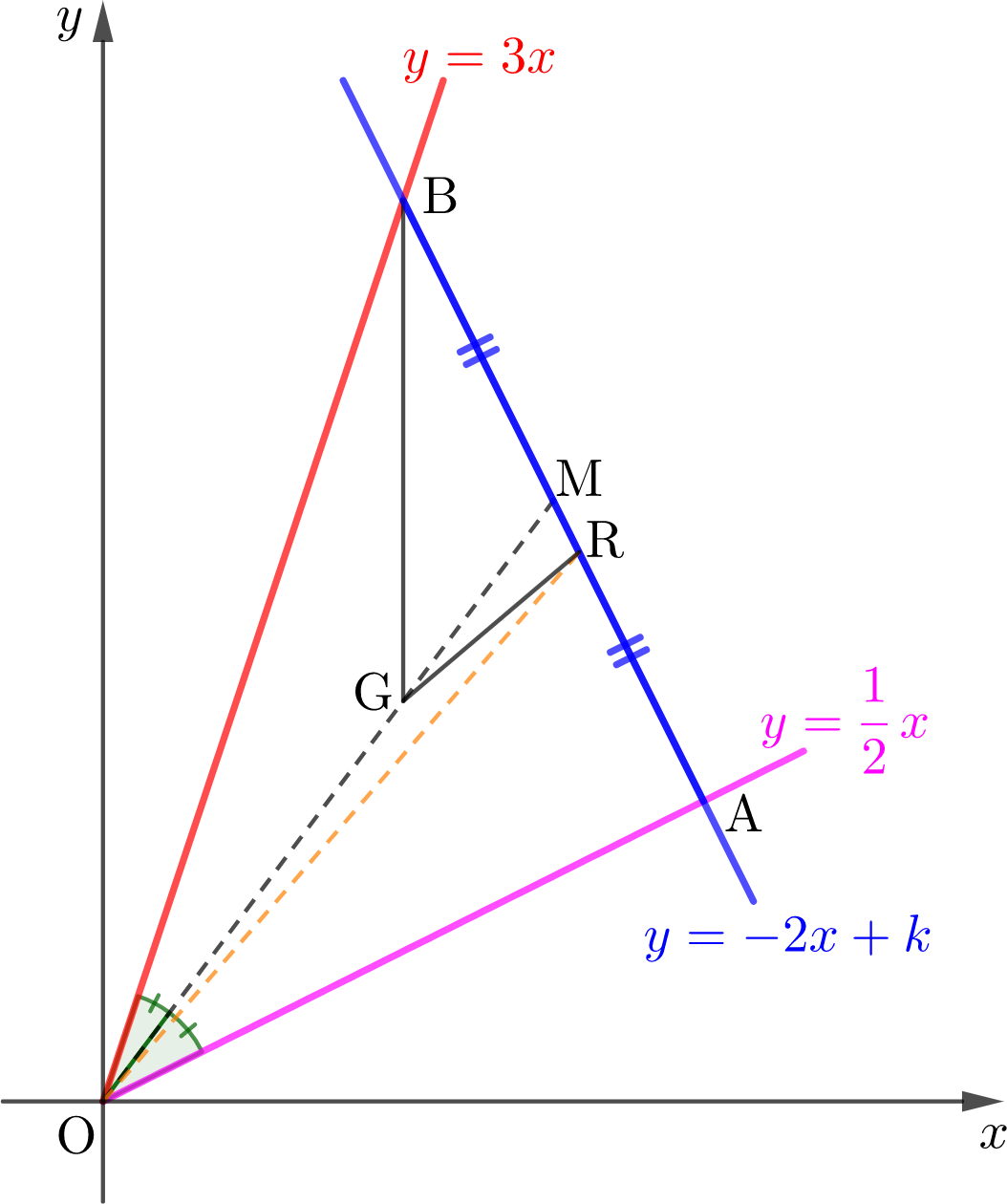
그림과 같이 두 직선 \(y=\frac{1}{2}x\)와 \(y=3x\)가 직선 \(y=-2x+k\)와 만나는 점을 각각 \(\mathrm{A,B}\)라 하자. 원점 \(\mathrm{O}\)와 두 점 \(\mathrm{A,B}\)를 꼭짓점으로 하는 삼각형 \(\mathrm{OAB}\)의 무게중심 좌표가 \(\mathrm{G}(3,4)\)일 때, 보기에서 옮은 것을 있는 대로 고른 것은?
\(\quad\)(ㄱ) 상수 \(k\)의 값은 15이다.
\(\quad\)(ㄴ) \(\angle \mathrm{AOB}\)의 이등분선과 선분 \(\mathrm{AB}\)의 교점을 \(\mathrm{R}\)이라 할 때, \(\mathrm{R}\)의 좌표는 \((5,5)\)이다.
\(\quad\)(ㄷ) \(\triangle\mathrm{ABO}\)의 넓이를 \(S_1\), \(\triangle\mathrm{BGR}\)의 넓이를 \(S_2\)라고 할 때, \(3S_2=(2-\sqrt{2})S_1\)을 만족한다.
응용예제3

그림과 같이 삼각형 \(\mathrm{ABC}\)에서 무게중심 \(\mathrm{G}\)의 좌표는 \(\left(1,\frac{4}{3}\right)\)이고, 직선 \(\mathrm{BC}\)의 방정식은 \(y=2x+1\)이다. 점 \(\mathrm{A}\)에서 변 \(\mathrm{BC}\)에 내린 수선의 발을 \(\mathrm{H}\)라 할 때, 선분 \(\mathrm{AH}\)의 길이를 구하시오.
응용예제4
삼각형 \(\rm{ABC}\)에서 선분 \(\rm{AB}\)의 연장선 위에 \(\rm{AQ=2BQ}\)를 만족시키는 점을 \(\rm Q\), 선분 \(\rm{BC}\) 위에 \(\rm{2BP=CP}\)를 만족시키는 점을 \(\rm Q\), 삼각형 \(\rm{ABC}\)의 무게중심을 \(\rm G\)라 할 때, 다음에서 옮은 것을 있는 대로 고른 것은?
\(\quad\)ㄱ. 선분 \(\rm{PQ}\)와 선분 \(\rm{AB}\)는 서로 평행하다.
\(\quad\)ㄴ. 점 \(\rm{P}\)는 삼각형 \(\rm{AQC}\)의 무게중심이다.
\(\quad\)ㄷ. 삼각형 \(\rm{ABC}\)의 넓이는 삼각형 \(\rm{BPG}\)의 넓이의 9배이다.



